Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T13:48:35.281Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermocapillary effects during the melting of phase-change materials in microgravity: steady and oscillatory flow regimes

Published online by Cambridge University Press:  07 December 2020

P. Salgado Sánchez Open the ORCID record for P. Salgado Sánchez [Opens in a new window] ,
J. M. Ezquerro ,
J. Fernández  and
J. Rodríguez Open the ORCID record for J. Rodríguez [Opens in a new window]
P. Salgado Sánchez*
Affiliation:
E-USOC, Center for Computational Simulation, Departamento de Aeronaves y Vehículos Espaciales, Escuela Técnica Superior de Ingeniería Aeronáutica y del Espacio, Universidad Politécnica de Madrid, Plaza Cardenal Cisneros 3, 28040Madrid, Spain
J. M. Ezquerro
Affiliation:
E-USOC, Center for Computational Simulation, Departamento de Aeronaves y Vehículos Espaciales, Escuela Técnica Superior de Ingeniería Aeronáutica y del Espacio, Universidad Politécnica de Madrid, Plaza Cardenal Cisneros 3, 28040Madrid, Spain
J. Fernández
Affiliation:
E-USOC, Center for Computational Simulation, Departamento de Matemática Aplicada a la Ingeniería Aeroespacial, Escuela Técnica Superior de Ingeniería Aeronáutica y del Espacio, Universidad Politécnica de Madrid, Plaza Cardenal Cisneros 3, 28040Madrid, Spain
J. Rodríguez
Affiliation:
E-USOC, Center for Computational Simulation, Departamento de Aeronaves y Vehículos Espaciales, Escuela Técnica Superior de Ingeniería Aeronáutica y del Espacio, Universidad Politécnica de Madrid, Plaza Cardenal Cisneros 3, 28040Madrid, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A detailed numerical investigation of thermocapillary effects during the melting of phase-change materials in microgravity is presented. The phase-change transition is analysed for the high-Prandtl-number material n-octadecane, which is enclosed in a two-dimensional rectangular container subjected to isothermal conditions along the lateral walls. The progression of the solid/liquid front during the melting leaves a free surface, where the thermocapillary effect acts driving convection in the liquid phase. 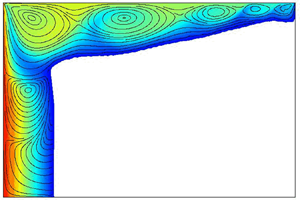The nature of the flow found during the melting depends on the container aspect ratio, $\varGamma$, and on the Marangoni number, $Ma$. For large $\varGamma$, this flow initially adopts a steady return flow structure characterised by a single large vortex, which splits into a series of smaller vortices to create a steady multicellular structure (SMC) with increasing $Ma$. At larger values of $Ma$, this SMC undergoes a transition to oscillatory flow through the appearance of a hydrothermal travelling wave (HTW), characterised by the creation of travelling vortices near the cold boundary. For small $\varGamma$, the thermocapillary flow at small to moderate $Ma$ is characterised by an SMC that develops initially within a thin layer near the free surface. At larger times, the SMC evolves into a large-scale steady vortical structure. With increasing applied $Ma$, a complex oscillatory mode is observed. This state, referred to as an oscillatory standing wave (OSW), is characterised by the pulsation of the vortical structure. Finally, for an intermediate $\varGamma$ both HTW and OSW modes can be found depending on $Ma$.

JFM classification

Convection: Marangoni convection Nonlinear Dynamical Systems: Pattern formation Phase change: Solidification/melting
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , A20
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agyenim, F., Eames, P. & Smyth, M. 2009 A comparison of heat transfer enhancement in a medium temperature thermal energy storage heat exchanger using fins. Solar Energy 83, 1509–1520.CrossRefGoogle Scholar
Alawadhi, E. M. 2008 Thermal analysis of a building brick containing phase change material. Energy Build. 40, 351–357.CrossRefGoogle Scholar
Atal, A., Wang, Y., Harsha, M. & Sengupta, S. 2016 Effect of porosity of conducting matrix on a phase change energy storage device. J. Heat Mass Transfer 93, 9–16.CrossRefGoogle Scholar
Bergeon, A., Henry, D., Benhadid, H. & Tuckerman, L. S. 1998 Marangoni convection in binary mixtures with Soret effect. J. Fluid Mech. 375, 143–177.Google Scholar
Brice, J. C. 1986 Crystal Growth. Blackie and Son.Google Scholar
Cabeza, L. F., Mehling, H., Hiebler, S. & Ziegler, F. 2002 Heat transfer enhancement in water when used as PCM in thermal energy storage. Appl. Therm. Engng 22, 1141–1151.CrossRefGoogle Scholar
Camp, D. W. 1977 National technical paper 1071-1080. NASA Technical Reports.Google Scholar
Carpenter, B. M. & Homsy, G. M. 1990 High Marangoni number convection in a square cavity: part II. Phys. Fluids 2, 137–149.CrossRefGoogle Scholar
Chub, C. H. & Wuest, W. 1979 Experiments on the transition from the steady to the oscillatory marangoni-convection of a floating zone under reduced gravity effect. Acta Astronaut. 6, 1073–1082.Google Scholar
Codina, R. 1993 A discontinuity-capturing crosswind-dissipation for the finite element solution of the convection-diffusion equation. Comput. Meth. Appl. Mech. Engng 110, 325–342.CrossRefGoogle Scholar
Creel, R. 2007 Apollo rover lessons learned: applying thermal control experiences on apollo lunar rover project to rovers for future space exploration.Google Scholar
Dhaidan, N. S. & Khodadadi, J. M. 2015 Melting and convection of phase change materials in different shape containers: a review. Renew. Sust. Energy Rev. 43, 449–477.CrossRefGoogle Scholar
Dhaidan, N. S., Khodadadi, J. M., Al-Hattab, T. A. & Al-Mashat, S. M. 2013 Experimental and numerical investigation of melting of NePCM inside an annular container under a constant heat flux including the effect of eccentricity. Intl J. Heat Mass Transfer 67, 455–468.CrossRefGoogle Scholar
Egolf, P. W. & Manz, H. 1994 Theory and modeling of phase change materials with and without mushy regions. Intl J. Heat Mass Transfer 37, 2917–2924.Google Scholar
Erhard, P. & Davis, S. H. 1991 Nonisothermal spreading of liquid drops on horizontal planes. J. Fluid Mech. 229, 365.CrossRefGoogle Scholar
Ettouney, H. M., Alatiqi, I., Al-Sahali, M. & Al-Ali, S. A. 2004 Heat transfer enhancement by metal screens and metal spheres in phase change energy storage systems. Renew. Energy 29, 841–860.CrossRefGoogle Scholar
Ezquerro, J. M., Bello, A., Salgado Sánchez, P., Laveron-Simavilla, A. & Lapuerta, V. 2019 The thermocapillary effects in phase change materials in microgravity experiment: design, preparation and execution of a parabolic flight experiment. Acta Astronaut. 162, 185–196.CrossRefGoogle Scholar
Ezquerro, J. M., Salgado Sánchez, P., Bello, A., Rodriguez, J., Lapuerta, V. & Laveron-Simavilla, A. 2020 Experimental evidence of thermocapillarity in phase change materials in microgravity: measuring the effect of marangoni convection in solid/liquid phase transitions. Intl Commun. Heat Mass Transfer 113, 104529.CrossRefGoogle Scholar
Fernandes, D., Pitie, F., Caceres, G. & Baeyens, J. 2012 Thermal energy storage: “how previous findings determine current research priorities”. Energy 39, 246–257.CrossRefGoogle Scholar
Gau, C. & Viskanta, R. 1986 Melting and solidification of a pure metal on a vertical wall. Trans. ASME 108, 174–181.Google Scholar
Giangi, M., Stella, F., Leonardi, E. & De Vahl Davis, G. 2002 A numerical study of solidification in the presence of a free surface under microgravity conditions. Numer. Heat Transfer A 57, 457–473.Google Scholar
Harari, I. & Hughes, T. 1992 What are C and h?: inequalities for the analysis and design of finite element methods. Comput. Meth. Appl. Mech. Engng 97, 157–192.Google Scholar
Ho, C. J. & Gaoe, J. Y. 2009 Preparation and thermophysical properties of nanoparticle-in-paraffin emulsion as phase change material. Intl Commun. Heat Mass Transfer 36, 467–470.Google Scholar
Hosseinizadeh, S. F., Rabienataj Darzi, A. A. & Tan, F. L. 2012 Numerical investigations of unconstrained melting of nano-enhanced phase change material (NEPCM) inside a spherical container. Intl J. Therm. Sci. 51, 77–83.CrossRefGoogle Scholar
Humphries, W. R. & Griggs, E. I. 1977 A design handbook for phase change thermal control and energy storage devices. Technical Publication 19780007491. NASA.Google Scholar
Khodadadi, J. M. & Zhang, Y. 2001 Effects of buoyancy-driven convection on melting within spherical containers. Intl J. Heat Mass Transfer 44, 1605–1618.Google Scholar
Kuhlmann, H. C. & Albensoeder, S. 2008 Three-dimensional flow instabilities in a thermocapillary-driven cavity. Phys. Rev. E 77, 036303.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon Books Ltd.Google Scholar
Lane, G. A. & Shamsundar, N. 1983 Solar heat storage: latent heat material – Volume 1: background and scientific principles. J. Solar Energy Eng. 105 (4), 467–467.Google Scholar
Lappa, M. 2018 On the formation and propagation of hydrothermal waves in liquid layers with phase change. Comput. Fluids 172, 741–760.Google Scholar
Lide, D. R. 2004 CRC Handbook of Chemistry and Physics: A Ready-Reference of Chemical and Physical Data, 85th edn (ed. D. R. Lide). CRC Press.Google Scholar
Madruga, S. & Mendoza, C. 2017 a Enhancement of heat transfer rate on phase change materials with thermocapillary flows. Eur. Phys. J. Spec. Top. 226, 1169–1176.CrossRefGoogle Scholar
Madruga, S. & Mendoza, C. 2017 b Heat transfer performance and melting dynamic of a phase change material subjected to thermocapillary effects. Intl J. Heat Mass Transfer 109, 501–510.CrossRefGoogle Scholar
Mills, K. C., Keene, B. J., Brooks, R. F. & Shirali, A. 1998 Marangoni effects in welding. Phil. Trans. R. Soc. Lond. A 356, 911–925.CrossRefGoogle Scholar
Montanero, J. M., Ferrero, C. & Shevtsova, V. M. 2008 Experimental study of the free surface deformation due to thermal convection in liquid bridges. Exp. Fluids 45, 1087–1101.CrossRefGoogle Scholar
Peltier, L. J. & Biringen, S. 1993 Time-dependent thermocapillary convection in a rectangular cavity: numerical results for a moderate Prandtl number fluid. J. Fluid Mech. 257, 339–357.CrossRefGoogle Scholar
Preisser, F., Schwabe, D. & Scharmann, A. 1983 Steady and oscillatory thermocapillary convection in liquid columns with free cylindrical surface. J. Fluid Mech. 126, 545–567.CrossRefGoogle Scholar
Roy, S. K. & Sengupta, S. 1990 Gravity-assisted melting in a spherical enclosure: effects of natural convection. Intl J. Heat Mass Transfer 33, 1135–1147.CrossRefGoogle Scholar
Salgado Sánchez, P., Ezquerro, J. M., Fernandez, J. & Rodriguez, J. 2020 a Thermocapillary effects during the melting of phase change materials in microgravity: heat transport enhancement. Intl J. Heat Mass Transfer 163, 120478.CrossRefGoogle Scholar
Salgado Sánchez, P., Ezquerro, J. M., Porter, J., Fernandez, J. & Tinao, I. 2020 b Effect of thermocapillary convection on the melting of phase change materials in microgravity: experiments and simulations. Intl J. Heat Mass Transfer 154, 119717.CrossRefGoogle Scholar
Samanta, S. K. 1987 Interdisciplinary Issues in Materials Processing and Manufacturing. American Society of Mechanical Engineers.Google Scholar
Schwabe, D. & Scharmann, A. 1979 Some evidence for the existence and magnitude of a critical marangoni number for the onset of oscillatory flow in crystal growth melts. J. Cryst. Growth 46, 125–131.CrossRefGoogle Scholar
Sen, A. K. & Davis, S. H. 1982 Steady thermocapillary flows in two-dimensional slots. J. Fluid Mech. 121, 163–186.Google Scholar
Shevtsova, V., Mialdun, A., Ferrera, C., Ermakov, M., Cabezas, M. G. & Montanero, J. M. 2008 Subcritical and oscillatory dynamic surface deformations in non-cylindrical liquid bridges. Fluid Dyn. Mater. Process. 4, 43–54.Google Scholar
Shevtsova, V., Nepomnyashchy, A. & Legros, J. C. 2003 Thermocapillary-buoyancy convection in a shallow cavity heated from the side. Phys. Rev. E 67, 066308.Google Scholar
Shokouhmand, H. & Kamkari, B. 2013 Experimental investigation on melting heat transfer characteristics of lauric acid in a rectangular thermal storage unit. Exp. Therm. Fluid Sci. 50, 201–212.CrossRefGoogle Scholar
Sirignano, W. A. & Glassman, I. 1970 Flame spreading above liquid fuels: surface tension driven flows. Combust. Sci. Technol. 1, 307.CrossRefGoogle Scholar
Smith, M. K. 1986 Instability mechanisms in dynamic thermocapillary liquid layers. Phys. Fluids 29, 3182.Google Scholar
Smith, M. K. & Davis, S. H. 1983 Instabilities of dynamic thermocapillary liquid layers. Part 1. Convective instabilities. J. Fluid Mech. 132, 119–144.Google Scholar
Strani, M., Piva, R. & Graziani, G. 1983 Thermocapillary convection in a rectangular cavity: asymptotic theory and numerical simulation. J. Fluid Mech. 130, 347–376.CrossRefGoogle Scholar
Subramanian, R. S. 1992 The motion of bubbles and drops in reduced gravity. In Transport Processes in Bubbles, Drops and particles. Hemisphere.CrossRefGoogle Scholar
Swanson, T. D. & Birur, G. C. 2003 Nasa thermal control technologies for robotic spacecraft. Appl. Therm. Engng. 23, 1055–1065.Google Scholar
Velez, C., Khayet, M. & Ortiz, J. M. 2015 Temperature-dependent thermal properties of solid/liquid phase change even-numbered n-alkanes: n-hexadecane, n-octadecane and n-eicosane. Appl. Energy 143, 383–394.Google Scholar
Voller, V. R., Cross, M. & Markatos, N. C. 1987 An enthalpy method for convection/diffusion phase change. Intl J. Numer. Meth. Engng 24, 271–284.CrossRefGoogle Scholar
Wang, Y., Amiri, A. & Vafai, K. 1999 An experimental investigation of the melting process in a rectangular enclosure. Intl J. Heat Mass Transfer 42, 3659–3672.CrossRefGoogle Scholar
Williams, J. P., Paige, D. A., Greenhagen, B. T. & Sefton-Nash, E. 2017 The global surface temperatures of the moon as measured by the diviner lunar radiometer experiment. Icarus 283, 300–325.CrossRefGoogle Scholar
Xiaohong, G., Xiange, S., Miao, Z. & Dawei, T. 2012 Influence of void ratio on thermal stress of pcm canister for heat pipe receiver. Appl. Therm. Engng 94, 615–621.Google Scholar
Zebib, A., Homsy, G. M. & Meiburg, E. 1985 High Marangoni number convection in a square cavity. Phys. Fluids 28, 3467–3476.CrossRefGoogle Scholar