Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schulz, Bernhard
and
Mellado, Juan Pedro
2018.
Wind Shear Effects on Radiatively and Evaporatively Driven Stratocumulus Tops.
Journal of the Atmospheric Sciences,
Vol. 75,
Issue. 9,
p.
3245.
Liang, Geng
Yu, Bin
Zhang, Bin
Xu, Hui
and
Liu, Hong
2019.
Hidden flow structures in compressible mixing layer and a quantitative analysis of entrainment based on Lagrangian method.
Journal of Hydrodynamics,
Vol. 31,
Issue. 2,
p.
256.
Haghshenas, Armin
and
Mellado, Juan Pedro
2019.
Characterization of wind-shear effects on entrainment in a convective boundary layer.
Journal of Fluid Mechanics,
Vol. 858,
Issue. ,
p.
145.
Parker, J. P.
Caulfield, C. P.
and
Kerswell, R. R.
2019.
Kelvin–Helmholtz billows above Richardson number .
Journal of Fluid Mechanics,
Vol. 879,
Issue. ,
Kirkpatrick, Michael P.
Williamson, N.
Armfield, S. W.
and
Zecevic, V.
2019.
Evolution of thermally stratified turbulent open channel flow after removal of the heat source.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
356.
Caulfield, Colm-cille P.
2020.
Open questions in turbulent stratified mixing: Do we even know what we do not know?.
Physical Review Fluids,
Vol. 5,
Issue. 11,
Mashayek, A.
Caulfield, C.P.
and
Alford, M.H.
2021.
Goldilocks mixing in oceanic shear-induced turbulent overturns.
Journal of Fluid Mechanics,
Vol. 928,
Issue. ,
Ivey, Gregory N.
Bluteau, Cynthia E.
Gayen, Bishakhdatta
Jones, Nicole L.
and
Sohail, Taimoor
2021.
Roles of Shear and Convection in Driving Mixing in the Ocean.
Geophysical Research Letters,
Vol. 48,
Issue. 3,
Caulfield, C.P.
2021.
Layering, Instabilities, and Mixing in Turbulent Stratified Flows.
Annual Review of Fluid Mechanics,
Vol. 53,
Issue. 1,
p.
113.
Cudby, Joshua
and
Lefauve, Adrien
2021.
Weakly nonlinear Holmboe waves.
Physical Review Fluids,
Vol. 6,
Issue. 2,
Lewin, S.F.
and
Caulfield, C.P.
2022.
Stratified turbulent mixing in oscillating shear flows.
Journal of Fluid Mechanics,
Vol. 944,
Issue. ,
Liu, Chih-Lun
Kaminski, Alexis K.
and
Smyth, William D.
2022.
The butterfly effect and the transition to turbulence in a stratified shear layer.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
Stastna, Marek
Deepwell, David
and
Grace, Andrew
2023.
Shear instability in mode-2 internal Kelvin waves.
Environmental Fluid Mechanics,
Vol. 23,
Issue. 2,
p.
407.
Zhu, Lu
Atoufi, Amir
Lefauve, Adrien
Kerswell, Rich R.
and
Linden, P.F.
2024.
Long-wave instabilities of sloping stratified exchange flows.
Journal of Fluid Mechanics,
Vol. 983,
Issue. ,
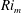 $Ri_{m}$ on the early time evolution of Kelvin–Helmholtz instability to its saturated ‘billow’ state. Even when the diffusion of the background velocity and density distributions is counterbalanced by artificial body forces to maintain the initial profiles, in the limit as
$Ri_{m}$ on the early time evolution of Kelvin–Helmholtz instability to its saturated ‘billow’ state. Even when the diffusion of the background velocity and density distributions is counterbalanced by artificial body forces to maintain the initial profiles, in the limit as 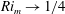 $Ri_{m}\rightarrow 1/4$, the perturbation growth rate tends to zero and the saturated perturbation energy becomes small. These results imply, at least for such canonical inflectional stratified shear flows, that ‘marginally unstable’ flows with
$Ri_{m}\rightarrow 1/4$, the perturbation growth rate tends to zero and the saturated perturbation energy becomes small. These results imply, at least for such canonical inflectional stratified shear flows, that ‘marginally unstable’ flows with 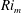 $Ri_{m}$ only slightly less than 1/4 are highly unlikely to become ‘turbulent’, in the specific sense of being associated with significantly enhanced dissipation, irreversible mixing and non-trivial modification of the background distributions without additional externally imposed forcing.
$Ri_{m}$ only slightly less than 1/4 are highly unlikely to become ‘turbulent’, in the specific sense of being associated with significantly enhanced dissipation, irreversible mixing and non-trivial modification of the background distributions without additional externally imposed forcing.


