Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tripathi, Manoj Kumar
Sahu, Kirti Chandra
and
Govindarajan, Rama
2015.
Dynamics of an initially spherical bubble rising in quiescent liquid.
Nature Communications,
Vol. 6,
Issue. 1,
Baczyzmalski, Dominik
Weier, Tom
Kähler, Christian J.
and
Cierpka, Christian
2015.
Near-wall measurements of the bubble- and Lorentz-force-driven convection at gas-evolving electrodes.
Experiments in Fluids,
Vol. 56,
Issue. 8,
Suñol, Francesc
and
González-Cinca, Ricard
2015.
Effects of gravity level on bubble formation and rise in low-viscosity liquids.
Physical Review E,
Vol. 91,
Issue. 5,
Cano-Lozano, José Carlos
Martínez-Bazán, Carlos
Magnaudet, Jacques
and
Tchoufag, Joël
2016.
Paths and wakes of deformable nearly spheroidal rising bubbles close to the transition to path instability.
Physical Review Fluids,
Vol. 1,
Issue. 5,
KUSUNO, Hiroaki
and
SANADA, Toshiyuki
2016.
Influence of Surfactants on the Motion of a Pair of Bubbles in Quiescent Liquids.
JAPANESE JOURNAL OF MULTIPHASE FLOW,
Vol. 29,
Issue. 5,
p.
515.
Li, Zhongchun
Zhao, Yang
Song, Xiaoming
Yu, Hongxing
Jiang, Shengyao
and
Ishii, Mamoru
2016.
Experimental investigation of single small bubble motion in linear shear flow in water.
Nuclear Engineering and Design,
Vol. 305,
Issue. ,
p.
334.
Cano-Lozano, José Carlos
Tchoufag, Joël
Magnaudet, Jacques
and
Martínez-Bazán, Carlos
2016.
A global stability approach to wake and path instabilities of nearly oblate spheroidal rising bubbles.
Physics of Fluids,
Vol. 28,
Issue. 1,
Joshi, Jyeshtharaj B.
Nandakumar, K.
Evans, Geoffrey M.
Pareek, Vishnu K.
Gumulya, Monica M.
Sathe, Mayur J.
and
Khanwale, Makrand A.
2017.
Bubble generated turbulence and direct numerical simulations.
Chemical Engineering Science,
Vol. 157,
Issue. ,
p.
26.
Wang, Shiyan
Guo, Tianqi
Dabiri, Sadegh
Vlachos, Pavlos P.
and
Ardekani, Arezoo M.
2017.
Effect of surfactant on bubble collisions on a free surface.
Physical Review Fluids,
Vol. 2,
Issue. 4,
Piedfert, Antoine
Lalanne, Benjamin
Masbernat, Olivier
and
Risso, Frédéric
2018.
Numerical simulations of a rising drop with shape oscillations in the presence of surfactants.
Physical Review Fluids,
Vol. 3,
Issue. 10,
Li, Chenliang
Zhang, A-Man
Wang, Shiping
and
Cui, Pu
2018.
Formation and coalescence of nanobubbles under controlled gas concentration and species.
AIP Advances,
Vol. 8,
Issue. 1,
Fei, Yang
and
Pang, Mingjun
2018.
The influence of interface contaminated degree on the wake characteristics of a spherical bubble at moderate Reynolds number under the condition of isothermal flow.
International Journal of Heat and Mass Transfer,
Vol. 121,
Issue. ,
p.
79.
Mathai, Varghese
Zhu, Xiaojue
Sun, Chao
and
Lohse, Detlef
2018.
Flutter to tumble transition of buoyant spheres triggered by rotational inertia changes.
Nature Communications,
Vol. 9,
Issue. 1,
Pesci, Chiara
Weiner, Andre
Marschall, Holger
and
Bothe, Dieter
2018.
Computational analysis of single rising bubbles influenced by soluble surfactant.
Journal of Fluid Mechanics,
Vol. 856,
Issue. ,
p.
709.
Song, Dong
Song, Baowei
Hu, Haibao
Du, Xiaosong
Du, Peng
Choi, Chang-Hwan
and
Rothstein, Jonathan P.
2018.
Effect of a surface tension gradient on the slip flow along a superhydrophobic air-water interface.
Physical Review Fluids,
Vol. 3,
Issue. 3,
Hosokawa, Shigeo
Hayashi, Kosuke
and
Tomiyama, Akio
2018.
Evaluation of adsorption of surfactant at a moving interface of a single spherical drop.
Experimental Thermal and Fluid Science,
Vol. 96,
Issue. ,
p.
397.
Senapati, Arahata
Singh, Gaurav
and
Lakkaraju, Rajaram
2019.
Numerical simulations of an inline rising unequal-sized bubble pair in a liquid column.
Chemical Engineering Science,
Vol. 208,
Issue. ,
p.
115159.
Lewandowski, Björn
Fertig, Micha
Ulbricht, Mathias
and
Krekel, Georg
2019.
Relationship between bubble characteristics and hydrodynamic parameters for single bubbles in presence of surface active agents.
Chemical Engineering Science,
Vol. 199,
Issue. ,
p.
179.
Zhang, Tingting
Qian, Yalan
Yin, Junlian
Zhang, Botao
and
Wang, Dezhong
2019.
Experimental study on 3D bubble shape evolution in swirl flow.
Experimental Thermal and Fluid Science,
Vol. 102,
Issue. ,
p.
368.
Lee, Wooram
and
Lee, Jae-Young
2020.
Experiment and modeling of lift force acting on single high Reynolds number bubbles rising in linear shear flow.
Experimental Thermal and Fluid Science,
Vol. 115,
Issue. ,
p.
110085.
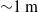 ${\sim }1~\mathrm{m} $. Experimental parameters are the diameter of the bubble and the surfactant concentration of 1-Pentanol or Triton X-100. We explore the surfactant effect on the drag and lift forces acting on the bubble in helical motion. While the drag force monotonically increases with the surfactant concentration as expected, the lift force shows a non-monotonic behaviour. Nevertheless, the direction of the lift force in a reference frame that rotates with the bubble along its trajectory is kept almost constant. We also observe the transient trajectory starting from helical motion to zigzag, which has never been reported in the case of purified water. The instantaneous amplitude and frequency of the transient motion agree with those of the motion regarded as steady. Finally the bubble motions are categorized as straight/helical/zigzag and experimentally examined in the field of two dimensionless numbers: Reynolds number
${\sim }1~\mathrm{m} $. Experimental parameters are the diameter of the bubble and the surfactant concentration of 1-Pentanol or Triton X-100. We explore the surfactant effect on the drag and lift forces acting on the bubble in helical motion. While the drag force monotonically increases with the surfactant concentration as expected, the lift force shows a non-monotonic behaviour. Nevertheless, the direction of the lift force in a reference frame that rotates with the bubble along its trajectory is kept almost constant. We also observe the transient trajectory starting from helical motion to zigzag, which has never been reported in the case of purified water. The instantaneous amplitude and frequency of the transient motion agree with those of the motion regarded as steady. Finally the bubble motions are categorized as straight/helical/zigzag and experimentally examined in the field of two dimensionless numbers: Reynolds number 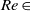 $\mathit{Re}\in $ [300 900] and the normalized drag coefficient
$\mathit{Re}\in $ [300 900] and the normalized drag coefficient 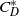 ${ C}_{D}^{\ast } $ which represents the slip condition. Remarkably it is found that the motions of a bubble with the intermediate slip conditions between free-slip and no-slip are helical for a broad range of
${ C}_{D}^{\ast } $ which represents the slip condition. Remarkably it is found that the motions of a bubble with the intermediate slip conditions between free-slip and no-slip are helical for a broad range of 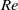 $\mathit{Re}$.
$\mathit{Re}$.