Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T17:18:05.593Z Has data issue: false hasContentIssue false
  • English
  • Français

Submersion of impacting spheres at low Bond and Weber numbers owing to a confined pool

Published online by Cambridge University Press:  05 December 2019

Han Chen ,
Hao-Ran Liu ,
Peng Gao Open the ORCID record for Peng Gao [Opens in a new window]  and
Hang Ding Open the ORCID record for Hang Ding [Opens in a new window]
Han Chen
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, China
Hao-Ran Liu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, China
Peng Gao
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, China
Hang Ding*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

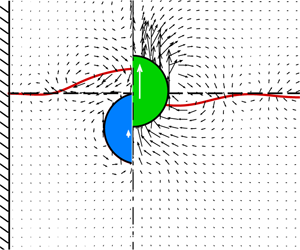
We numerically investigate the mechanism resulting in fate change of a hydrophobic sphere impacting onto a confined pool, that is, at the same impact speed, it does not submerge in a wide pool but does in a narrow pool. We find that the reflection of the impact-induced gravity-capillary waves from the pool boundary is responsible for this phenomenon. In particular, the return of the wave to the symmetry axis may coincide with the rising of the impacting sphere to the water surface, which corresponds to the critical conditions of the fate change. Moreover, for the spheres at the onset of submersion in a wide pool, our analysis suggests that this scenario also accounts for an interesting observation in the numerical simulations. That is, the effective pool size $S_{c}$, beyond which the submersion of impacting spheres is no longer affected by the pool size $S$, is mainly dependent on the sphere diameter, no matter whether the surface waves are the capillary or gravity waves. For $S<S_{c}$, two important pool sizes ($S_{w,1}$ and $S_{w,2}$, and $S_{w,2}\geqslant S_{w,1}$) are identified at the same impact speed, and the sphere submersion takes place at $S_{w,1}\leqslant S\leqslant S_{w,2}$. Based on the flow features identified in simulations, a scaling law is proposed to correlate the Weber number and Bond number with $S_{w}$. The theoretical prediction is shown to agree well with the numerical results.

JFM classification

Interfacial Flows (free surface): Contact lines Waves/Free-surface Flows: Capillary waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A13
Check for updates
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acheson, D. J. 1990 Elementary Fluid Dynamics. Oxford University Press.Google Scholar
Aristoff, J. M. & Bush, J. W. 2009 Water entry of small hydrophobic spheres. J. Fluid Mech. 619, 45–78.CrossRefGoogle Scholar
Aristoff, J. M., Truscott, T. T., Techet, A. H. & Bush, J. W. 2010 The water entry of decelerating spheres. Phys. Fluids 22, 032102.CrossRefGoogle Scholar
Chang, B., Myeong, J., Virot, E., Clanet, C., Kim, H. Y. & Jung, S. 2019 Jumping dynamics of aquatic animals. J. R. Soc. Interface 16, 20190014.CrossRefGoogle ScholarPubMed
Chen, H., Liu, H. R., Lu, X. Y. & Ding, H. 2018 Entrapping an impacting particle at a liquid–gas interface. J. Fluid Mech. 841, 1073–1084.CrossRefGoogle Scholar
Gao, P. & Feng, J. J. 2011 A numerical investigation of the propulsion of water walkers. J. Fluid Mech. 668, 363–383.CrossRefGoogle Scholar
Hu, D. L. & Bush, J. W. 2010 The hydrodynamics of water-walking arthropods. J. Fluid Mech. 644, 5–33.CrossRefGoogle Scholar
Jaworek, A., Balachandran, W., Krupa, A., Kulon, J. & Lackowski, M. 2006 Wet electroscrubbers for state of the art gas cleaning. Environ. Sci. Technol. 40, 6197–6207.CrossRefGoogle ScholarPubMed
Kim, S. J., Hasanyan, J., Gemmell, B. J., Lee, S. & Jung, S. 2015 Dynamic criteria of plankton jumping out of water. J. R. Soc. Interface 12, 20150582.CrossRefGoogle ScholarPubMed
Koh, J. S., Yang, E., Jung, G. P., Jung, S. P., Son, J. H., Lee, S. I., Jablonski, P. G., Wood, R. J., Kim, H. Y. & Cho, K. J. 2015 Jumping on water: Surface tension–dominated jumping of water striders and robotic insects. Science 349, 517–521.CrossRefGoogle ScholarPubMed
Lee, D. G. & Kim, H. Y. 2008 Impact of a superhydrophobic sphere onto water. Langmuir 24, 142–145.CrossRefGoogle ScholarPubMed
Lighthill, J. 2001 Waves in Fluids. Cambridge University Press.Google Scholar
Liu, D., He, Q. & Evans, G. 2014 Capture of impacting particles on a confined gas–liquid interface. Mineral. Engng 55, 138–146.CrossRefGoogle Scholar
Liu, H. R. & Ding, H. 2015 A diffuse-interface immersed-boundary method for two-dimensional simulation of flows with moving contact lines on curved substrates. J. Comput. Phys. 294, 484–502.CrossRefGoogle Scholar
Liu, H. R., Gao, P. & Ding, H. 2017 Fluid–structure interaction involving dynamic wetting: 2D modeling and simulations. J. Comput. Phys. 348, 45–65.CrossRefGoogle Scholar
Mansoor, M. M., Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2014 Water entry without surface seal: extended cavity formation. J. Fluid Mech. 743, 295–326.CrossRefGoogle Scholar
Marston, J. O., Truscott, T. T., Speirs, N. B., Mansoor, M. M. & Thoroddsen, S. T. 2016 Crown sealing and buckling instability during water entry of spheres. J. Fluid Mech. 794, 506–529.CrossRefGoogle Scholar
Raphaël, E. & De Gennes, P. G. 1996 Capillary gravity waves caused by a moving disturbance: wave resistance. Phys. Rev. E 53, 3448.Google ScholarPubMed
Speirs, N. B., Mansoor, M. M., Belden, J. & Truscott, T. T. 2019 Water entry of spheres with various contact angles. J. Fluid Mech. 862, R3.CrossRefGoogle Scholar
Ueda, Y., Tanaka, M., Uemura, T. & Iguchi, M. 2010 Water entry of a superhydrophobic low-density sphere. J. Vis. 13, 289–292.CrossRefGoogle Scholar
Vella, D., Lee, D. G. & Kim, H. Y. 2006 Sinking of a horizontal cylinder. Langmuir 22, 2972–2974.CrossRefGoogle ScholarPubMed
Wang, A., Song, Q. & Yao, Q. 2015 Behavior of hydrophobic micron particles impacting on droplet surface. Atmos. Environ. 115, 1–8.CrossRefGoogle Scholar

Chen et al. supplementary movie 1

Dynamics of an impacting sphere at θ=108Ο, λρ=0.855, Bo=3.4, We=13.5 and Re=2200. The sphere ends up with sinking in a small pool (left and S=3.5) while floating at the interface in a large one (right and S=20).

Download Chen et al. supplementary movie 1(Video)
Video 8.6 MB

Chen et al. supplementary movie 2

Dynamics of an impacting sphere at θ=150Ο, λρ=1.2, Bo=0.5, We=23 and Re=1800. The sphere ends up with sinking in a small pool (left and S=3.5) while bouncing from the interface in a large one (right and S=20).

Download Chen et al. supplementary movie 2(Video)
Video 10.2 MB