Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-02T21:11:56.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Subgrid-scale structure and fluxes of turbulence underneath a surface wave

Published online by Cambridge University Press:  18 September 2019

Kuanyu Chen ,
Minping Wan Open the ORCID record for Minping Wan [Opens in a new window] ,
Lian-Ping Wang  and
Shiyi Chen
Kuanyu Chen
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing 100871, PR China
Minping Wan*
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China
Lian-Ping Wang
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China Department of Mechanical Engineering, University of Delaware, Newark, DE 19716, USA
Shiyi Chen*
Affiliation:
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing 100871, PR China Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, the behaviours of subgrid-scale (SGS) turbulence are investigated with direct numerical simulations when an isotropic turbulence is brought to interact with imposed rapid waves. A partition of the velocity field is used to decompose the SGS stress into three parts, namely, the turbulent part 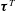$\unicode[STIX]{x1D749}^{T}$, the wave-induced part 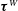$\unicode[STIX]{x1D749}^{W}$ and the cross-interaction part 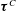$\unicode[STIX]{x1D749}^{C}$. Under strong wave straining, 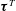$\unicode[STIX]{x1D749}^{T}$ is found to follow the Kolmogorov scaling 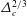$\unicode[STIX]{x1D6E5}_{c}^{2/3}$, where 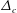$\unicode[STIX]{x1D6E5}_{c}$ is the filter width. Based on the linear Airy wave theory, 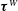$\unicode[STIX]{x1D749}^{W}$ and the filtered strain-rate tensor due to the wave motion, 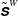$\tilde{\unicode[STIX]{x1D64E}}^{W}$, are found to have different phases, posing a difficulty in applying the usual eddy-viscosity model. On the other hand, 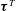$\unicode[STIX]{x1D749}^{T}$ and the filtered strain-rate tensor due to the turbulent motion, 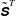$\tilde{\unicode[STIX]{x1D64E}}^{T}$, are only weakly wave-phase-dependent and could be well related by an eddy-viscosity model. The linear wave theory is also used to describe the vertical distributions of SGS statistics driven by the wave-induced motion. The predictions are in good agreement with the direct numerical simulation results. The budget equation for the turbulent SGS kinetic energy shows that the transport terms related to turbulence are important near the free surface and they compensate the imbalance between the energy flux and the SGS energy dissipation.

JFM classification

Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 768 - 795
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. G. & McIntyre, M. E. 1988 An exact theory of nonlinear waves on a Lagrangian-mean flow. J. Fluid Mech. 89, 609–646.Google Scholar
Anis, A. & Moum, J. N. 1995 Surface wave-turbulence interactions: scaling 𝜀(z) near the sea surface. J. Phys. Oceanogr. 25, 2025–2045.Google Scholar
Babanin, A. V. 2006 On a wave-induced turbulence and a wave-mixed upper ocean layer. Geophys. Res. Lett. 33, L20605.Google Scholar
Brumley, B. H. & Jirka, G. H. 1987 Near-surface turbulence in a grid-stirred tank. J. Fluid Mech. 183, 235–263.Google Scholar
Chen, S., Meneveau, C. & Katz, J. 2006 Scale interactions of turbulence subjected to a straining-relaxation-destraining cycle. J. Fluid Mech. 562, 123–150.Google Scholar
Craik, A. D. D. & Leibovich, S. 1976 A rational model for langmuir circulations. J. Fluid Mech. 73, 401–426.Google Scholar
D’Asaro, E. 2014 Turbulence in the upper-ocean mixed layer. Annu. Rev. Fluid Mech. 6, 101–115.Google Scholar
Forristall, G. Z. 1981 Measurements of a saturated range in ocean wave spectra. J. Geophys. Res. 86, 8075–8084.Google Scholar
Fulgosi, M. D., Lakehal, D., Banerjee, S. & Angleis, V. D. 2003 Durect numerical simulation of turbulence in a sheared air–water flow with a deformable interface. J. Fluid Mech. 482, 319–345.Google Scholar
Green, T., Medwin, H. & Paquin, J. E. 1972 Measurements of surface wave decay due to underwater turbulence. Nat. Phys. Sci. 237, 115–117.Google Scholar
Guo, X. & Shen, L. 2009 On the generation and maintenance of waves and turbulence in simulations of free-surface turbulence. J. Comput. Phys. 228, 7313–7332.Google Scholar
Guo, X. & Shen, L. 2013 Numerical study of the effect of surface waves on turbulence underneath. Part 1. Mean flow and turbulence vorticity. J. Fluid Mech. 733, 558–587.Google Scholar
Guo, X. & Shen, L. 2014 Numerical study of the effect of surface waves on turbulence underneath. Part 2. Eulerian and Lagrangian properties of turbulence kinetic energy. J. Fluid Mech. 744, 250–272.Google Scholar
He, U., Howell, R. & Walsh, J. 1993 Measurement of ocean wave spectra using narrow-beam he radar. IEEE J. Ocean. Engng 18, 296–305.Google Scholar
Hodges, B. R. & Street, R. L. 1999 On simulation of turbulent nonlinear free-surface flows. J. Comput. Phys. 151, 425–457.Google Scholar
Huang, C. & Qiao, F. 2010 Wave turbulence interaction and its induced mixing in the upper ocean. J. Geophys. Res. Oceans 115, 1–12.Google Scholar
Hunt, J. & Graham, J. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84, 209–235.Google Scholar
Jiang, J. & Street, R. 1991 Modulated flows beneath wind-ruffled, mechanically generated water waves. J. Geophys. Res. 96, 2711–2721.Google Scholar
Kitaigorodskii, S. A. & Lumley, J. L. 1983 Wave-turbulence interactions in the upper ocean. Part 2. Statistical characteristics of wave and turbulence components of the random velocity field in the marine surface layer. J. Phys. Oceanogr. 13, 1988–1999.Google Scholar
Komori, A., Kursose, R., Iwano, K., Ukai, T. & Naoya, S. 2010 Direct numerical simulation of wind-driven, turbulence and sclar transfer at sheard gass–liquid interface. J. Turbul. 11, 1–20.Google Scholar
Leibovich, S. 1977a Convective instability of stably stratified water in the ocean. J. Fluid Mech. 82, 561–585.Google Scholar
Leibovich, S. 1977b On the evolution of the system of wind drift currents and langmuir circulations in the ocean. Part 1. Theory and the averaged current. J. Fluid Mech. 79, 715–743.Google Scholar
Lighthill, M. J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Lin, M., Moeng, C., Tsai, W., Sullivan, P. P. & Belcher, S. E. 2008 Direct numerical simulation of wind-wave generation processes. J. Fluid Mech. 616, 1–30.Google Scholar
Liu, S., Katz, J. & Meneveau, C. 1999 Evolution and modelling of subgrid scales during rapid straining of turbulence. J. Fluid Mech. 387, 281–320.Google Scholar
Lundgren, T.2003 Linearly forced isotropic turbulence. Tech. Rep. 461, Center for Turbulence Research.Google Scholar
Melville, W., Shear, R. & Veron, F. 1998 Laboratory measurements of the generation and evolution of langmuir circulations. J. Fluid Mech. 364, 31–58.Google Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulations. Annu. Rev. Fluid Mech. 32, 1–32.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Trans. R. Soc. Lond. A 331, 735–800.Google Scholar
Rosales, C. & Meneveau, C. 2005 Linear forcing in numerical simulations of isotropic turbulence: physical space implementations and convergence properties. Phys. Fluids 17, 1–8.Google Scholar
Shen, L. & Yue, D. K. P. 2001 Large-eddy simulation of free-surface turbulence. J. Fluid Mech. 440, 75–116.Google Scholar
Shen, L., Zhang, X., Yue, D. K. P. & Triantafyllou, G. S. 1999 The surface layer for free-surface turbulent flows. J. Fluid Mech. 386, 167–212.Google Scholar
Sullivan, P. & McWilliams, J. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.Google Scholar
Teixeira, M. A. C. & Belcher, S. E. 2002 On the distortion of turbulence by a progressive surface wave. J. Fluid Mech. 458, 229–267.Google Scholar
Thais, L. & Magnaudet, J. 1996 Turbulent structure beneath surface gravity waves sheared by the wind. J. Fluid Mech. 328, 313–344.Google Scholar
Walker, D. T., Leighton, R. I. & Garza-Rios, L. O. 1996 Shear-free turbulence near a flat free surface. J. Fluid Mech. 320, 19–51.Google Scholar
Wang, W. & Huang, R. X. 2004 Wind energy input to the surface waves. J. Phys. Oceanogr. 34, 1276–1280.Google Scholar
Wright, J. W. 1977 Detection of ocean waves by microwave radar; the modulation of short gravity-capillary waves. Bound. Layer Meteorol. 13, 87–105.Google Scholar
Yan, S. & Ma, Q. 2010 Numerical simulation of interaction between wind and 2D freak waves. Eur. J. Mech. (B/Fluids) 29, 18–31.Google Scholar
Yang, D. & Shen, L. 2010 Direct-simulation based study of turbulent flow over various waving boundaries. J. Fluid Mech. 650, 131–180.Google Scholar
Yu, D. & Girimaji, S. 2006 Direct numerical simulations of homogeneous turbulence subject to periodic shear. J. Fluid Mech. 566, 117–151.Google Scholar
Zou, Q. & Chen, H. 2017 Wind and current effects on extreme wave formation and breaking. J. Phys. Oceanogr. 47, 1817–1841.Google Scholar
Supplementary material: File

Chen et al. supplementary material

Chen et al. supplementary material

Download Chen et al. supplementary material(File)
File 45.9 KB