Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T00:48:10.890Z Has data issue: false hasContentIssue false
  • English
  • Français

Subcritical magnetohydrodynamic instabilities: Chandrasekhar’s theorem revisited

Published online by Cambridge University Press:  11 November 2019

Kengo Deguchi Open the ORCID record for Kengo Deguchi [Opens in a new window]
Kengo Deguchi*
Affiliation:
School of Mathematics, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

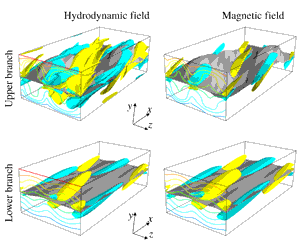
Subcritical instabilities (i.e. finite-amplitude instabilities that occur without any linear instability) in magnetohydrodynamic (MHD) flows are studied by computing finite-amplitude equilibrium solutions of viscous–resistive MHD equations. The plane Couette flow magnetised by a uniform spanwise current is used as a model flow. Solutions are found for broad sub- and super-Alfvénic flow regimes by controlling the magnetic Mach number, but their existence is greatly influenced by the magnetic Prandtl number. When that number is unity, and the walls are perfectly insulating, the solution branch found in the super-Alfvénic regime cannot be continued towards the sub-Alfvénic regime; the boundary between those regimes is called the Chandrasekhar state, where Chandrasekhar (Proc. Natl Acad. Sci. USA, vol. 42, 1956, pp. 273–276) proved the non-existence of a linear ideal instability. Thus, the result may seem to suggest that the Chandrasekhar theorem holds even when diffusivity and nonlinearity are present. This is certainly true, but only when the perturbation magnetic field on the boundary is small. The boundary effects add more complexity to the nonlinear analysis of the Chandrasekhar state. The Chandrasekhar theorem is known to work for flows bounded by perfectly conducting walls. However, somewhat paradoxically, when the walls are perfectly conducting, our large-Reynolds-number computational results show that the nonlinear solutions do exist in the Chandrasekhar state. We give a theoretical reasoning for this curious phenomenon, using a large-Reynolds-number asymptotic analysis. For small magnetic Prandtl numbers, we also show that the solution can be continued for infinitesimally small magnetic Mach number, where the flow is significantly sub-Alfvénic.

JFM classification

Instability: Nonlinear instability Nonlinear Dynamical Systems: Bifurcation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 882 , 10 January 2020 , A20
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balbus, S. & Hawley, J. F. 1991 A powerful local shear instability in weakly magnetised disks. I. Linear analysis. Astrophys. J. 376, 214–222.Google Scholar
Bogdanova-Ryzhova, E. V. & Ryzhov, O. S. 1994 On singular solutons of the incompressible boundary-layer equation including a point of vanishing skin friction. Acta Mechanica 4, 27–37.Google Scholar
Braginsky, S. 1964 Self excitation of a magnetic field during the motion of a highly conducting fluid. Sov. Phys. JETP 20, 726–735.Google Scholar
Chandrasekhar, S. 1956 On the stability of the simplest solution of the equations of hydromagnetics. Proc. Natl Acad. Sci. USA A 42, 273–276.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Chen, Q., Otto, A. & Lee, L. C. 1997 Tearing instability, Kelvin–Helmholtz instability, and magnetic reconnection. J. Geophys. Res. 102A1, 151–161.Google Scholar
Clever, R. M. & Busse, F. H. 1992 Three-dimensional convection in a horizontal fluid layer subjected to a constant shear. J. Fluid Mech. 234, 511–527.Google Scholar
Cline, K. S., Brummell, N. H. & Cattaneo, F. 2003 Dynamo action driven by shear and magnetic buoyancy. Astrophys. J. 599, 1449–1468.Google Scholar
Davidson, P. A. 2001 An Introduction to Magnetohydrodynamics. Cambridge University Press.Google Scholar
Deguchi, K. 2015 Self-sustained states at Kolmogorov microscale. J. Fluid Mech. 781, R6.Google Scholar
Deguchi, K. 2017 Scaling of small vortices in stably stratified shear flows. J. Fluid Mech. 821, 582–594.Google Scholar
Deguchi, K. 2019a High-speed shear driven dynamos. Part 1. Asymptotic analysis. J. Fluid Mech. 868, 176–211.Google Scholar
Deguchi, K. 2019b High-speed shear driven dynamos. Part 2. Numerical analysis. J. Fluid Mech. 876, 830–858.Google Scholar
Deguchi, K. & Hall, P. 2016 On the instability of vortex-wave interaction states. J. Fluid Mech. 802, 634–666.Google Scholar
De Lozar, A., Melibovsky, F., Avila, M. & Hof, B. 2012 Edge state in pipe flow experiments. Phys. Rev. Lett. 108, 214502.Google Scholar
Einaudi, G. & Rubini, F. 1986 Resistive instabilities in a flowing plasma: I. Inviscid case. Phys. Fluids 29, 2563–2568.Google Scholar
Gellert, M., Rüdiger, G., Schultz, M., Guseva, A. & Hollerbach, R. 2016 Nonaxisymmetric MHD instabilities of Chandrasekhar states in Taylor–Couette geometry. Astrophys. J. 823, 99–1–9.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 1–24.Google Scholar
Goossens, M., Ruderman, M. S. & Hollweg, J. V. 1995 Dissipative MHD solutions for resonant Alfvén waves in 1-dimensional magnetic flux tubes. Solar Phys. 157, 75–102.Google Scholar
Guseva, A., Hollerbach, R., Willis, A. P. & Avila, M. 2017 Dynamo action in a quasi-Keplerian Taylor–Couette flow. Phys. Rev. Lett. 119, 164501.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Hof, B., van Doorne, C. W., Westerweel, J., Nieuwstadt, F. T., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305 (5690), 1594–1598.Google Scholar
Hollerbach, R. & Rüdiger, G. 2005 New type of magnetorotational instability in cylindrical Taylor–Couette flow. Phys. Rev. Lett. 95, 124501.Google Scholar
Itano, T. & Generalis, S. 2009 Hairpin vortex solution in planar Couette flow: a tapestry of knotted vortices. Phys. Rev. Lett. 102, 114501.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.Google Scholar
Joseph, D. D. 1966 Nonlinear stability of the Boussinesq equations by the method of energy. Arch. Rat. Mech. Anal. 22, 163–184.Google Scholar
Kirillov, O. N. 2017 Singular diffusionless limits of double-diffusive instabilities in magnetohydrodynamics. Proc. R. Soc. Lond. A 473 (2205), 20170344.Google Scholar
Krause, F. & Rädler, K.-H. 1980 Mean-field Magnetohydrodynamics and Dynamo. Akademié and Pergamon.Google Scholar
Miura, A. & Pritchett, P. L. 1982 Nonlocal stability analysis of the MHD Kelvin–Helmholtz instability in a compressible plasma. J. Geophys. Res. 87, 7431–7444.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Ofman, L., Morrison, P. J. & Steinolfson, R. S. 1993 Nonlinear evolution of resistive tearing mode instability with shear flow and viscosity. Phys. Fluids B 5 (2), 376–387.Google Scholar
Rincon, F., Ogilvie, G. I. & Proctor, M. R. E. 2007 Self-sustaining nonlinear dynamo process in Keplerian shear flows. Phys. Rev. Lett. 98, 254502.Google Scholar
Riols, A., Rincon, F., Cossu, C., Lesur, G., Longaretti, P.-Y., Ogilvie, G. I. & Herault, J. 2013 Global bifurcations to subcritical magnetorotational dynamo action in Keplerian shear flow. J. Fluid Mech. 731, 1–45.Google Scholar
Roberts, P. H. 1964 The stability of hydromagnetic Couette flow. Proc. Camb. Phil. Soc. 60, 635–651.Google Scholar
Rüdiger, G., Gellert, M., Hollerbach, R., Schultz, J. & Stefani, F. 2018 Stability and instability of hydromagnetic Taylor–Couette flows. Phys. Rep. 741, 1–89.Google Scholar
Rüdiger, G., Schultz, M., Stefani, F. & Mond, M. 2015 Diffusive magnetohydrodynamic instabilities beyond the Chandrasekhar theorem. Astrophys. J. 811, 84–1–7.Google Scholar
Sakurai, T., Goossens, M. & Hollweg, J. V. 1991 Resonant behaviour of MHD waves on magnetic flux tubes. I. Connection formulae at the resonant surfaces. Solar Phys. 133, 227–245.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Tataronis, J. A. & Mond, M. 1987 Magnetohydrodynamic stability of plasmas with aligned mass flow. Phys. Fluids 30, 84–89.Google Scholar
Tobias, S. M. & Cattaneo, F. 2013 Shear-driven dynamo waves at high magnetic Reynolds number. Nature 497, 463465.Google Scholar
Teed, R. J. & Proctor, M. R. E. 2017 Quasi-cyclic behaviour in non-linear simulations of the shear dynamo. Mon. Not. R. Astron. Soc. 467, 48584864.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.Google Scholar
Vaz, R. H., Boshier, F. A. T. & Mestel, A. J. 2018 Dynamos in an annulus with fields linear in the axial coordinate. Geophys. Astrophys. Fluid Dyn. 112, 222–234.Google Scholar
Wang, J., Gibson, J. F. & Waleffe, F. 2007 Lower branch coherent states: transition and control. Phys. Rev. Lett. 98, 204501.Google Scholar
Yousef, T. A., Heinemann, T., Schekochihin, A. A., Kleeorin, N., Rogachevskii, I., Iskakov, A. B., Cowley, S. C. & McWilliams, J. C. 2008 Generation of magnetic field by combined action of turbulence and shear. Phys. Rev. Lett. 100, 184501.Google Scholar