Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T18:33:34.448Z Has data issue: false hasContentIssue false
  • English
  • Français

Strouhal–Reynolds number relationship for flow past a circular cylinder

Published online by Cambridge University Press:  26 October 2017

Hongyi Jiang Open the ORCID record for Hongyi Jiang [Opens in a new window]  and
Liang Cheng
Hongyi Jiang
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Liang Cheng*
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia DUT-UWA Joint Research Centre, State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, 116024, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

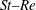The Strouhal–Reynolds number ($St{-}Re$) relationship for flow past a circular cylinder in the low 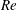$Re$ range of 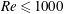$Re\leqslant 1000$ is investigated through two- (2D) and three-dimensional (3D) direct numerical simulations (DNS). An improved method is proposed for the determination of the separating velocity and the wake width to allow for a better estimation of the wake Strouhal number 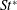$St^{\ast }$. For 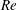$Re$ in the extended laminar regime calculated by 2D DNS, the 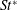$St^{\ast }$ values are found to be more uniform than the original 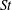$St$ for the 2D flow. It is also found that the 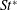$St^{\ast }$ values for the 2D and 3D flows agree well in the laminar regime of 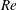$Re$ up to approximately 270. In addition, uniform 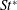$St^{\ast }$ values are also obtained for different mode A and mode B flow structures triggered artificially by using different cylinder span lengths in DNS. It is demonstrated that the drop in 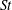$St$ (with respect to its 2D counterpart) with the development of different 3D wake structures is due to the decrease in the separating velocity and the increase in the wake width for a 3D flow, rather than the existence of a particular wake structure such as pure mode A or vortex dislocation. However, as the wake flow becomes increasingly turbulent with further increase in 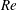$Re$, the 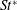$St^{\ast }$ value for the 3D flow increases gradually and deviates from its 2D counterpart, since for turbulent 3D flows the vortex shedding frequency scales on a length smaller than the wake width.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 170 - 188
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Fey, U., König, M. & Eckelmann, H. 1998 A new Strouhal–Reynolds-number relationship for the circular cylinder in the range 47 < Re < 2 × 105 . Phys. Fluids 10, 1547–1549.CrossRefGoogle Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.CrossRefGoogle Scholar
Issa, R. I. 1986 Solution of implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.CrossRefGoogle Scholar
Jiang, H., Cheng, L. & An, H. 2017c On numerical aspects of simulating flow past a circular cylinder. Intl J. Numer. Meth. Fluids 85, 113–132.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017a Two- and three-dimensional instabilities in the wake of a circular cylinder near a moving wall. J. Fluid Mech. 812, 435–462.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S. & An, H. 2017b Three-dimensional wake transition for a circular cylinder near a moving wall. J. Fluid Mech. 818, 260–287.CrossRefGoogle Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016 Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.CrossRefGoogle Scholar
Monkewitz, P. A. 1988 The absolute and convective nature of instability in two-dimensional wakes at low Reynolds numbers. Phys. Fluids 31, 999–1006.CrossRefGoogle Scholar
Noca, F., Park, H. & Gharib, M. 1998 Vortex formation length of a circular cylinder (300 < Re < 4000) using DPIV. Proceedings on Bluff Body Wakes and Vortex-Induced Vibration. ASME Fluids Engineering Division.Google Scholar
Norberg, C. 1994 An experimental investigation of the flow around a circular cylinder: influence of aspect ratio. J. Fluid Mech. 258, 287–316.CrossRefGoogle Scholar
Papaioannou, G. V., Yue, D. K. P., Triantafyllou, M. S. & Karniadakis, G. E. 2006 Three-dimensionality effects in flow around two tandem cylinders. J. Fluid Mech. 558, 387–413.CrossRefGoogle Scholar
Ponta, F. L. 2006 Effect of shear-layer thickness on the Strouhal–Reynolds number relationship for bluff-body wakes. J. Fluids Struct. 22, 1133–1138.CrossRefGoogle Scholar
Ponta, F. L. & Aref, H. 2004 Strouhal–Reynolds number relationship for vortex streets. Phys. Rev. Lett. 93, 084501.CrossRefGoogle ScholarPubMed
Roshko, A.1954 On the development of turbulent wakes from vortex streets. National Advisory Committee for Aeronautics Report 1191.Google Scholar
Roshko, A. 1955 On the wake and drag of bluff bodies. J. Aeronaut. Sci. 22, 124–132.CrossRefGoogle Scholar
Roushan, P. & Wu, X. L. 2005 Structure-based interpretation of the Strouhal–Reynolds number relationship. Phys. Rev. Lett. 94, 054504.CrossRefGoogle ScholarPubMed
Schewe, G. 1983 On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 133, 265–285.CrossRefGoogle Scholar
Tong, F., Cheng, L. & Zhao, M. 2015 Numerical simulations of steady flow past two cylinders in staggered arrangements. J. Fluid Mech. 765, 114–149.CrossRefGoogle Scholar
Williamson, C. H. K. 1996a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C. H. K. 1996b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Williamson, C. H. K. & Brown, G. L. 1998 A series in 1/√Re to represent the Strouhal–Reynolds number relationship of the cylinder wake. J. Fluids Struct. 12, 1073–1085.CrossRefGoogle Scholar