Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-02T19:01:45.243Z Has data issue: false hasContentIssue false
  • English
  • Français

Stress relaxation in a dilute bacterial suspension: the active–passive transition

Published online by Cambridge University Press:  15 May 2019

Sankalp Nambiar ,
Phanikanth S. ,
P. R. Nott  and
Ganesh Subramanian Open the ORCID record for Ganesh Subramanian [Opens in a new window]
Sankalp Nambiar
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore 560064, India
Phanikanth S.
Affiliation:
Department of Chemical Engineering, IISc, Bangalore 560012, India
P. R. Nott
Affiliation:
Department of Chemical Engineering, IISc, Bangalore 560012, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore 560064, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper follows a recent article of Nambiar et al. (J. Fluid Mech., vol. 812, 2017, pp. 41–64) on the linear rheological response of a dilute bacterial suspension (e.g. E. coli) to impulsive starting and stopping of simple shear flow. Here, we analyse the time dependent nonlinear rheology for a pair of linear flows – simple shear (a canonical weak flow) and uniaxial extension (a canonical strong flow), again in response to impulsive initiation and cessation. The rheology is governed by the bacterium orientation distribution which satisfies a kinetic equation that includes rotation by the imposed flow, and relaxation to isotropy via rotary diffusion and tumbling. The relevant dimensionless parameters are the Péclet number 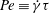$Pe\equiv \dot{\unicode[STIX]{x1D6FE}}\unicode[STIX]{x1D70F}$, which dictates the importance of flow-induced orientation anisotropy, and 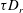$\unicode[STIX]{x1D70F}D_{r}$, which quantifies the relative importance of the two intrinsic orientation decorrelation mechanisms (tumbling and rotary diffusion). Here, $\unicode[STIX]{x1D70F}$ is the mean run duration of a bacterium that exhibits a run-and-tumble dynamics, 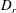$D_{r}$ is the intrinsic rotary diffusivity of the bacterium and 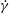$\dot{\unicode[STIX]{x1D6FE}}$ is the characteristic magnitude of the imposed velocity gradient. The solution of the kinetic equation is obtained numerically using a spectral Galerkin method, that yields the rheological properties (the shear viscosity, the first and second normal stress differences for simple shear, and the extensional viscosity for uniaxial extension) over the entire range of 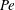$Pe$. For simple shear, we find that the stress relaxation predicted by our analysis at small 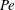$Pe$ is in good agreement with the experimental observations of Lopez et al. (Phys. Rev. Lett., vol. 115, 2015, 028301). However, the analysis at large 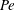$Pe$ yields relaxations that are qualitatively different. Upon step initiation of shear, the rheological response in the experiments corresponds to a transition from a nearly isotropic suspension of active swimmers at small 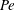$Pe$, to an apparently (nearly) isotropic suspension of passive rods at large 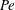$Pe$. In contrast, the computations yield the expected transition to a nearly flow-aligned suspension of passive rigid rods at high 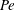$Pe$. We probe this active–passive transition systematically, complementing the numerical solution with analytical solutions obtained from perturbation expansions about appropriate base states. Our study suggests courses for future experimental and analytical studies that will help understand relaxation phenomena in active suspensions.

JFM classification

Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 1072 - 1104
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1970 Handbook of Mathematical Functions. Dover.Google Scholar
Arfken, G. B. & Weber, H. J. 2013 Mathematical Methods for Physicists. Elsevier.Google Scholar
Bechtel, T. M. & Khair, A. S. 2017 Linear viscoelasticity of a dilute active suspension. Rheol. Acta 56 (2), 149–160.Google Scholar
Becker, L. E. & Shelley, M. J. 2001 Instability of elastic filaments in shear flow yields first-normal-stress differences. Phys. Rev. Lett. 87 (19), 198301.Google Scholar
Berg, H. C. 1993 Random Walks in Biology. Princeton University Press.Google Scholar
Brenner, H. 1974 Rheology of a dilute suspension of axisymmetric brownian particles. Intl J. Multiphase Flow 1 (2), 195–341.Google Scholar
Chen, D. T. N., Lau, A. W. C., Hough, L. A., Islam, M. F., Goulian, M., Lubensky, T. C. & Yodh, A. G. 2007 Fluctuations and rheology in active bacterial suspensions. Phys. Rev. Lett. 99, 148302.Google Scholar
Chen, S. B. & Koch, D. L. 1996 Rheology of dilute suspensions of charged fibers. Phys. Fluids 8 (11), 2792–2807.Google Scholar
Clement, E., Lindner, A., Douarche, C. & Auradou, H. 2016 Bacterial suspensions under flow. Eur. Phys. J. 225 (11–12), 2389–2406.Google Scholar
Darnton, N. C. & Berg, H. C. 2007 Force-extension measurements on bacterial flagella: triggering polymorphic transformations. Biophys. J. 92 (6), 2230–2236.Google Scholar
Doi, M. & Edwards, S. F. 1978 Dynamics of rod-like macromolecules in concentrated solution. Part 2. J. Chem. Soc. Faraday Trans. 74, 918–932.Google Scholar
Gachelin, J., Mino, G., Berthet, H., Lindner, A., Rousselet, A. & Clément, E. 2013 Non-Newtonian viscosity of escherichia coli suspensions. Phys. Rev. Lett. 110 (26), 268103.Google Scholar
Hinch, E. J. & Leal, L. G. 1973 Time-dependent shear flows of a suspension of particles with weak Brownian rotations. J. Fluid Mech. 57 (4), 753–767.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102 (715), 161–179.Google Scholar
Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.Google Scholar
Krishnamurthy, D. & Subramanian, G. 2015 Collective motion in a suspension of micro-swimmers that run-and-tumble and rotary diffuse. J. Fluid Mech. 781, 422–466.Google Scholar
Laxminarsimharao, V., Garg, P. & Subramanian, G. 2018 Concentration banding instability of a sheared bacterial suspension. Phys. Rev. Lett. (submitted) arXiv:1808.07805.Google Scholar
Leal, L. G. & Hinch, E. J. 1972 The rheology of a suspension of nearly spherical particles subject to brownian rotations. J. Fluid Mech. 55 (4), 745–765.Google Scholar
Loisy, A., Eggers, J. & Liverpool, T. B. 2018 Active suspensions have non-monotonic flow curves and multiple mechanical equilibria. Phys. Rev. Lett. 121, 018001.Google Scholar
Lopez, H. M., Gachelin, J., Douarche, C., Auradou, H. & Clement, E. 2015 Turning bacteria suspensions into superfluids. Phys. Rev. Lett. 115, 028301.Google Scholar
Marchetti, M. C., Joanny, J. F., Ramaswamy, S., Liverpool, T. B., Prost, J., Rao, M. & Simha, A. R. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143–1189.Google Scholar
McDonnell, A. G., Gopesh, T. C., Lo, J., O’Bryan, M., Yeo, L. Y., Friend, J. R. & Ranganathan, P. 2015 Motility induced changes in viscosity of suspensions of swimming microbes in extensional flows. Soft Matt. 11 (23), 4658–4668.Google Scholar
Messiah, A. 1958 Quantum Mechanics Vol. I and Vol. II. Dover.Google Scholar
Nambiar, S., Nott, P. R. & Subramanian, G. 2017 Stress relaxation in a dilute bacterial suspension. J. Fluid Mech. 812, 41–64.Google Scholar
Ramaswamy, S. 2010 The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 1, 323–345.Google Scholar
Saintillan, D. 2010a The dilute rheology of swimming suspensions: a simple kinetic model. Exp. Mech. 50, 1275–1281.Google Scholar
Saintillan, D. 2010b Extensional rheology of active suspensions. Phys. Rev. E 81 (5), 056307.Google Scholar
Saintillan, D. 2018 Rheology of active fluids. Annu. Rev. Fluid Mech. 50, 563–592.Google Scholar
Saintillan, D. & Shelley, M. J. 2008 Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100 (17), 178103.Google Scholar
Scheraga, H. A. 1955 Non-Newtonian viscosity of solutions of ellipsoidal particles. J. Chem. Phys. 23 (8), 1526–1532.Google Scholar
Scheraga, H. A., Edsall, J. T. & Gadd, J. O. Jr 1951 Double refraction of flow: numerical evaluation of extinction angle and birefringence as a function of velocity gradient. J. Chem. Phys. 19 (9), 1101–1108.Google Scholar
Sokolov, A. & Aranson, I. S. 2009 Reduction of viscosity in suspension of swimming bacteria. Phys. Rev. Lett. 103, 148101.Google Scholar
Stenhammar, J., Nardini, C., Nash, R. W., Marenduzzo, D. & Morozov, A. 2017 Role of correlations in the collective behavior of microswimmer suspensions. Phys. Rev. Lett. 119 (2), 028005.Google Scholar
Stewart, W. E. & Sorensen, J. P. 1972 Hydrodynamic interaction effects in rigid dumbbell suspensions. Part II. Computations for steady shear flow. Trans. Soc. Rheol. 16 (1), 1–13.Google Scholar
Strand, S. R., Kim, S. & Karrila, S. J. 1987 Computation of rheological properties of suspensions of rigid rods: stress growth after inception of steady shear flow. J. Non-Newtonian Fluid Mech. 24 (3), 311–329.Google Scholar
Subramanian, G. & Brady, J. F. 2004 A Chapman–Enskog formalism for inertial suspensions. Physica A 334 (3–4), 385–416.Google Scholar
Subramanian, G. & Koch, D. L. 2009 Critical bacterial concentration for the onset of collective swimming. J. Fluid Mech. 632, 359–400.Google Scholar
Subramanian, G. & Nott, P. R. 2011 The fluid dynamics of swimming microorganisms and cells. IISc J. 91, 283–313.Google Scholar
Takatori, S. C. & Brady, J. F. 2017 Superfluid behavior of active suspensions from diffusive stretching. Phys. Rev. Lett. 118, 018003.Google Scholar
Underhill, P. T., Hernandez-Ortiz, J. P. & Graham, M. D. 2008 Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 100 (24), 248101.Google Scholar