Article contents
Stokes flow singularity at the junction between impermeable and porous walls
Published online by Cambridge University Press: 24 October 2012
Abstract
For two-dimensional, creeping flow in a half-plane, we consider the singularity that arises at an abrupt transition in permeability from zero to a finite value along the wall, where the pressure is coupled to the seepage flux by Darcy’s law. This problem represents the junction between the impermeable wall of the inflow section and the porous membrane further downstream in a spiral-wound desalination module. On a macroscopic, outer length scale the singularity appears like a jump discontinuity in normal velocity, characterized by a non-integrable 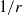 $1/ r$ divergence of the pressure. This far-field solution is imposed as the boundary condition along a semicircular arc of dimensionless radius 30 (referred to the microscopic, inner length scale). A preliminary numerical solution (using a least-squares variant of the method of fundamental solutions) indicates a continuous normal velocity along the wall coupled with a weaker
$1/ r$ divergence of the pressure. This far-field solution is imposed as the boundary condition along a semicircular arc of dimensionless radius 30 (referred to the microscopic, inner length scale). A preliminary numerical solution (using a least-squares variant of the method of fundamental solutions) indicates a continuous normal velocity along the wall coupled with a weaker  $1/ \sqrt{r} $ singularity in the pressure. However, inconsistencies in the numerically imposed outer boundary condition indicate a very slow radial decay. We undertake asymptotic analysis to: (i) understand the radial decay behaviour; and (ii) find a more accurate far-field solution to impose as the outer boundary condition. Similarity solutions (involving a stream function that varies like some power of
$1/ \sqrt{r} $ singularity in the pressure. However, inconsistencies in the numerically imposed outer boundary condition indicate a very slow radial decay. We undertake asymptotic analysis to: (i) understand the radial decay behaviour; and (ii) find a more accurate far-field solution to impose as the outer boundary condition. Similarity solutions (involving a stream function that varies like some power of  $r$) are insufficient to satisfy all boundary conditions along the wall, so we generalize these by introducing linear and quadratic terms in
$r$) are insufficient to satisfy all boundary conditions along the wall, so we generalize these by introducing linear and quadratic terms in 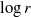 $\log r$. By iterating on the wall boundary conditions (analogous to the method of reflections), the outer asymptotic series is developed through second order. We then use a hybrid computational scheme in which the numerics are iteratively patched to the outer asymptotics, thereby determining two free coefficients in the latter. We also derive an inner asymptotic series and fit its free coefficient to the numerics at
$\log r$. By iterating on the wall boundary conditions (analogous to the method of reflections), the outer asymptotic series is developed through second order. We then use a hybrid computational scheme in which the numerics are iteratively patched to the outer asymptotics, thereby determining two free coefficients in the latter. We also derive an inner asymptotic series and fit its free coefficient to the numerics at 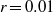 $r= 0. 01$. This enables evaluation of the singular flow field in the limit as
$r= 0. 01$. This enables evaluation of the singular flow field in the limit as 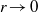 $r\ensuremath{\rightarrow} 0$. Finally, a uniformly valid fit is obtained with analytical formulas. The singular flow field for a solid–porous abutment and the general Stokes flow solutions obtained in the asymptotic analysis are programmed in Fortran for future use as local basis functions in computational schemes. Numerics are required for the intermediate-
$r\ensuremath{\rightarrow} 0$. Finally, a uniformly valid fit is obtained with analytical formulas. The singular flow field for a solid–porous abutment and the general Stokes flow solutions obtained in the asymptotic analysis are programmed in Fortran for future use as local basis functions in computational schemes. Numerics are required for the intermediate- $r$ regime because the inner and outer asymptotic expansions do not extend far enough toward each other to enable rigorous asymptotic matching. The logarithmic correction terms explain why the leading far-field solution (used in the preliminary numerics) was insufficient even at very large distances.
$r$ regime because the inner and outer asymptotic expansions do not extend far enough toward each other to enable rigorous asymptotic matching. The logarithmic correction terms explain why the leading far-field solution (used in the preliminary numerics) was insufficient even at very large distances.
- Type
- Papers
- Information
- Copyright
- ©2012 Cambridge University Press
References
- 6
- Cited by


