Article contents
Steady and unsteady modelling of the float height of a rotating air hockey disk
Published online by Cambridge University Press: 30 July 2015
Abstract
A similarity reduction of the Navier–Stokes equations for the motion of an infinite rotating disk above an air-bearing table yields a coupled pair of ordinary differential equations governed by a Reynolds number 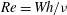 $Re=Wh/{\it\nu}$ and a rotation parameter
$Re=Wh/{\it\nu}$ and a rotation parameter 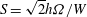 $S=\sqrt{2}h{\it\Omega}/W$, where
$S=\sqrt{2}h{\it\Omega}/W$, where 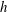 $h$ is the float height,
$h$ is the float height, 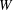 $W$ is the air levitation velocity,
$W$ is the air levitation velocity, 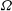 ${\it\Omega}$ is the disk rotation rate, and
${\it\Omega}$ is the disk rotation rate, and  ${\it\nu}$ is the kinematic viscosity of air. After deriving the small- and large-Reynolds-number behaviour of solutions, the equations are numerically integrated over a wide range of
${\it\nu}$ is the kinematic viscosity of air. After deriving the small- and large-Reynolds-number behaviour of solutions, the equations are numerically integrated over a wide range of 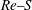 $Re{-}S$ parameter space. Zero-lift boundaries are computed as well as the boundaries separating pure outward flow from counter-flow in the gap. The theory is used to model the steady float height of a finite-radius air hockey disk under the assumption that the float height is small relative to the diameter of the disk and the flow is everywhere laminar. The steady results are tested against direct numerical simulation (DNS) of the unsteady axisymmetric Navier–Stokes equations for the cases where the disk rotates at constant angular velocity but is either at a fixed height or free to move axially. While a constant shift in the gap pressure conforms closely to that found using steady theory, the interaction of the radial jet emanating from the gap with a vertical transpiration field produces vortex rings which themselves propagate around to interact with the jet. Although these structures diffuse as they propagate up and away from the gap, they induce a departure from the steady-flow assumption of atmospheric pressure at the gap exit, thus inducing small irregular axial oscillations of the floating disk.
$Re{-}S$ parameter space. Zero-lift boundaries are computed as well as the boundaries separating pure outward flow from counter-flow in the gap. The theory is used to model the steady float height of a finite-radius air hockey disk under the assumption that the float height is small relative to the diameter of the disk and the flow is everywhere laminar. The steady results are tested against direct numerical simulation (DNS) of the unsteady axisymmetric Navier–Stokes equations for the cases where the disk rotates at constant angular velocity but is either at a fixed height or free to move axially. While a constant shift in the gap pressure conforms closely to that found using steady theory, the interaction of the radial jet emanating from the gap with a vertical transpiration field produces vortex rings which themselves propagate around to interact with the jet. Although these structures diffuse as they propagate up and away from the gap, they induce a departure from the steady-flow assumption of atmospheric pressure at the gap exit, thus inducing small irregular axial oscillations of the floating disk.
JFM classification
- Type
- Papers
- Information
- Copyright
- © Cambridge University Press 2015. This is a work of the U.S. Government and is not subject to copyright protection in the United States.
References
- 2
- Cited by


