Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T07:17:46.851Z Has data issue: false hasContentIssue false
  • English
  • Français

Statics and dynamics of a viscous ligament drawn out of a pure-liquid bath

Published online by Cambridge University Press:  07 July 2021

Xiaofeng Wei ,
Javier Rivero-Rodríguez Open the ORCID record for Javier Rivero-Rodríguez [Opens in a new window] ,
Jun Zou Open the ORCID record for Jun Zou [Opens in a new window]  and
Benoit Scheid Open the ORCID record for Benoit Scheid [Opens in a new window]
Xiaofeng Wei
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, PR China
Javier Rivero-Rodríguez
Affiliation:
TIPs – Fluid Physics Unit, Université Libre de Bruxelles, C.P. 165/67, 1050Brussels, Belgium Escuela Técnica Superior de Ingenieros Industriales, Universidad de Málaga, Plaza El Ejido s/n, 29013Málaga, Spain
Jun Zou*
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, Hangzhou 310027, PR China
Benoit Scheid*
Affiliation:
TIPs – Fluid Physics Unit, Université Libre de Bruxelles, C.P. 165/67, 1050Brussels, Belgium
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

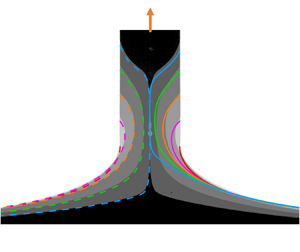
In this paper we investigate the statics and the dynamics of large-viscosity ligaments attached to a rod and drawn out of a pure-liquid bath. Following the similar work of films pulling out of a bath (Champougny et al., J. Fluid Mech., vol. 811, 2017, pp. 499–524), a one-dimensional model is applied to describe the ligaments drawn at constant velocities. We focus on the whole drawing dynamics of the ligament up to breakup, for which the breakup height is determined. The breakup height coincides with the maximum static meniscus height for very slow drawing, whose process can be described by quasi-static solutions. We present the numerical results of the static menisci and analytically unravel the mechanism in the low gravity case. Starting from a stable static meniscus, the breakup height of faster drawing depends separately on the rod radius and the drawing velocity, the latter dependency being fully determined by considering the agravic limit. Next, it is shown that the entire lifetime of the ligament drawing can be sequenced into a ductility stage, a capillarity stage and a pinch-off stage, the latter being shown to be almost instantaneous. The ductility and capillarity stages are decorrelated with the help of an approximate solution of the ductility stage, and the transition between the two stages corresponds to the time at which the capillarity-induced contraction velocity exceeds the ductility-induced one. The one-dimensional predictions of the breakup height and the entrained liquid volume attached to the rod quantitatively agree with experimental results of silicone oil ligaments, and the deviations are rationalized in comparison with a two-dimensional model.

JFM classification

Interfacial Flows (free surface): Liquid bridges Low-Reynolds-number flows: Slender-body theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 922 , 10 September 2021 , A14
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abkarian, M. & Stone, H.A. 2020 Stretching and break-up of saliva filaments during speech: A route for pathogen aerosolization and its potential mitigation. Phys. Rev. Fluids 5 (10), 102301.CrossRefGoogle Scholar
Augello, L. 2015 Instability of two-phase co-axial jets at small Reynolds number. PhD thesis, EPFL.Google Scholar
Bechert, M. & Scheid, B. 2017 Combined influence of inertia, gravity, and surface tension on the linear stability of Newtonian fiber spinning. Phys. Rev. Fluids 2 (11), 113905.CrossRefGoogle Scholar
Benilov, E.S. & Cummins, C.P. 2013 The stability of a static liquid column pulled out of an infinite pool. Phys. Fluids 25 (11), 112105.CrossRefGoogle Scholar
Benilov, E.S. & Oron, A. 2010 The height of a static liquid column pulled out of an infinite pool. Phys. Fluids 22 (10), 102101.CrossRefGoogle Scholar
Brulin, S., Tropea, C. & Roisman, I. 2020 Pinch-off of a viscous liquid bridge stretched with high Reynolds numbers. Colloids Surf. A 587, 124271.CrossRefGoogle Scholar
Champougny, L., Rio, E., Restagno, F. & Scheid, B. 2017 The break-up of free films pulled out of a pure liquid bath. J. Fluid Mech. 811, 499–524.CrossRefGoogle Scholar
Clanet, C. & Lasheras, J.C. 1999 Transition from dripping to jetting. J. Fluid Mech. 383, 307–326.CrossRefGoogle Scholar
Clasen, C., Eggers, J., Fontelos, M.A., Li, J. & Mckinley, G.H. 2006 The beads-on-string structure of viscoelastic threads. J. Fluid Mech. 556, 283–308.CrossRefGoogle Scholar
Day, R.F., Hinch, E.J. & Lister, J.R. 1998 Self-similar capillary pinchoff of an inviscid fluid. Phys. Rev. Lett. 80, 704–707.CrossRefGoogle Scholar
Dewandre, A., Rivero-Rodriguez, J., Vitry, Y., Sobac, B. & Scheid, B. 2020 Microfluidic droplet generation based on non-embedded co-flow-focusing using 3D printed nozzle. Sci. Rep. 10 (1), 21616.CrossRefGoogle ScholarPubMed
Eggers, J. 1993 Universal pinching of 3D axisymmetric free-surface flow. Phys. Rev. Lett. 71, 3458–3460.CrossRefGoogle ScholarPubMed
Eggers, J. 2005 Drop formation – an overview. Z. Angew. Math. Mech. 85 (6), 400–410.CrossRefGoogle Scholar
Eggers, J. & Dupont, T.F. 1994 Drop formation in a one-dimensional approximation of the Navier–Stokes equation. J. Fluid Mech. 262, 205–221.CrossRefGoogle Scholar
Evangelio, A., Campo-Cortés, F. & Gordillo, J.M. 2016 Simple and double microemulsions via the capillary breakup of highly stretched liquid jets. J. Fluid Mech. 804, 550–577.CrossRefGoogle Scholar
Frankel, I. & Weihs, D. 1985 Stability of a capillary jet with linearly increasing axial velocity (with application to shaped charges). J. Fluid Mech. 155, 289–307.CrossRefGoogle Scholar
Frankel, I. & Weihs, D. 1987 Influence of viscosity on the capillary instability of a stretching jet. J. Fluid Mech. 185, 361–383.CrossRefGoogle Scholar
Gart, S., Socha, J.J., Vlachos, P.P. & Jung, S. 2015 Dogs lap using acceleration-driven open pumping. Proc. Natl Acad. Sci. 112 (52), 15798–15802.CrossRefGoogle ScholarPubMed
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena. Springer.CrossRefGoogle Scholar
Gordillo, J.M., Sevilla, A. & Campo-Cortés, F. 2014 Global stability of stretched jets: conditions for the generation of monodisperse micro-emulsions using coflows. J. Fluid Mech. 738, 335–357.CrossRefGoogle Scholar
Griffiths, I.M. & Howell, P.D. 2008 Mathematical modelling of non-axisymmetric capillary tube drawing. J. Fluid Mech. 605, 181–206.CrossRefGoogle Scholar
Heller, M. 2008 Numerical study of free surfaces and particle sorting in microfluidic systems. PhD thesis, Technical University of Denmark.Google Scholar
Henderson, D., Segur, H., Smolka, L.B. & Wadati, M. 2000 The motion of a falling liquid filament. Phys. Fluids 12 (3), 550–565.CrossRefGoogle Scholar
van Hoeve, W., Gekle, S., Snoeijer, J.H., Versluis, M., Brenner, M.P. & Lohse, D. 2010 Breakup of diminutive Rayleigh jets. Phys. Fluids 22 (12), 122003.CrossRefGoogle Scholar
Huerre, P & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Ide, Y. & White, J.L. 1976 The spinnability of polymer fluid filaments. J. Appl. Polym. Sci. 20 (9), 2511–2531.CrossRefGoogle Scholar
James, D.F. 1974 The meniscus on the outside of a small circular cylinder. J. Fluid Mech. 63 (4), 657–664.CrossRefGoogle Scholar
Javadi, A., Eggers, J., Bonn, D., Habibi, M. & Ribe, N.M. 2013 Delayed capillary breakup of falling viscous jets. Phys. Rev. Lett. 110, 144501.CrossRefGoogle ScholarPubMed
Jimenez, L.N., Martínez Narváez, C.D.V. & Sharma, V. 2020 Capillary breakup and extensional rheology response of food thickener cellulose gum NaCMC in salt-free and excess salt solutions. Phys. Fluids 32 (1), 012113.CrossRefGoogle Scholar
Keller, J.B., Rubinow, S.I. & Tu, Y.O. 1973 Spatial instability of a jet. Phys. Fluids 16 (12), 2052–2055.CrossRefGoogle Scholar
Kim, W. & Bush, J.W.M. 2012 Natural drinking strategies. J. Fluid Mech. 705, 7–25.CrossRefGoogle Scholar
Kim, S.J., Kim, S. & Jung, S. 2018 Extremes of the pinch-off location and time in a liquid column by an accelerating solid sphere. Phys. Rev. Fluids 3 (8), 084001.CrossRefGoogle Scholar
Kofman, N., Rohlfs, W., Gallaire, F., Scheid, B. & Ruyer-Quil, C. 2018 Prediction of two-dimensional dripping onset of a liquid film under an inclined plane. Intl J. Multiphase Flow 104, 286–293.CrossRefGoogle Scholar
Kovitz, A.A. 1975 Static fluid interfaces external to a right circular cylinder–experiment and theory. J. Colloid Interface Sci. 50, 125–142.CrossRefGoogle Scholar
Kumar, S. 2015 Liquid transfer in printing processes: liquid bridges with moving contact lines. Annu. Rev. Fluid Mech. 47 (1), 67–94.CrossRefGoogle Scholar
Lambert, P., Seigneur, F., Koelemeijer, S. & Jacot, J. 2006 A case study of surface tension gripping: the watch bearing. J. Micromech. Microengng 16 (7), 1267–1276.CrossRefGoogle Scholar
Landau, L. & Levich, B. 1942 Dragging of a liquid by a moving plate. Acta Physicochim. USSR 17, 42–54.Google Scholar
Li, Y. & Sprittles, J.E. 2016 Capillary breakup of a liquid bridge: identifying regimes and transitions. J. Fluid Mech. 797, 29–59.CrossRefGoogle Scholar
Marmottant, P. & Villermaux, E. 2004 Fragmentation of stretched liquid ligaments. Phys. Fluids 16 (8), 2732–2741.CrossRefGoogle Scholar
Martínez-Calvo, A., Rivero-Rodríguez, J., Scheid, B. & Sevilla, A. 2020 Natural break-up and satellite formation regimes of surfactant-laden liquid threads. J. Fluid Mech. 883, A35.CrossRefGoogle Scholar
Martínez-Calvo, A., Rubio-Rubio, M. & Sevilla, A. 2018 The nonlinear states of viscous capillary jets confined in the axial direction. J. Fluid Mech. 834, 335–358.CrossRefGoogle Scholar
Owens, M.S., Vinjamur, M., Scriven, L.E. & Macosko, C.W. 2011 Misting of Newtonian liquids in forward roll coating. Ind. Engng Chem. Res. 50 (6), 3212–3219.CrossRefGoogle Scholar
Padday, J. & Pitt, A. 1973 The stability of axisymmetric menisci. Phil. Trans. R. Soc. A 275, 489–528.Google Scholar
Padday, J.F., Pétré, G., Rusu, C.G., Gamero, J. & Wozniak, G. 1997 The shape, stability and breakage of pendant liquid bridges. J. Fluid Mech. 352, 177–204.CrossRefGoogle Scholar
Papageorgiou, D.T. 1995 On the breakup of viscous liquid threads. Phys. Fluids 7 (7), 1529–1544.CrossRefGoogle Scholar
Pitts, E. 1976 The stability of a meniscus joining a vertical rod to a bath of liquid. J. Fluid Mech. 76 (4), 641–651.CrossRefGoogle Scholar
Rayleigh, Lord 1878 On the instability of jets. Proc. Lond. Math. Soc. s1-10 (1), 4–13.CrossRefGoogle Scholar
Rayleigh, Lord 1892 XVI. On the instability of a cylinder of viscous liquid under capillary force. Lond. Edinburgh Dublin Phil. Mag. J. Sci. 34 (207), 145–154.CrossRefGoogle Scholar
Reis, P.M., Jung, S., Aristoff, J.M. & Stocker, R. 2010 How cats lap: water uptake by felis catus. Science 330 (6008), 1231–1234.CrossRefGoogle ScholarPubMed
Rivero-Rodriguez, J., Perez-Saborid, M. & Scheid, B. 2021 An alternative choice of the boundary condition for the arbitrary Lagrangian–Eulerian method. J. Comput. Phys. 443, 110494.CrossRefGoogle Scholar
Rubio-Rubio, M., Sevilla, A. & Gordillo, J.M. 2013 On the thinnest steady threads obtained by gravitational stretching of capillary jets. J. Fluid Mech. 729, 471–483.CrossRefGoogle Scholar
Ryck, A. & Quéré, D. 1996 Inertial coating of a fibre. J. Fluid Mech. 311, 219–237.CrossRefGoogle Scholar
Scheid, B., Delacotte, J., Dollet, B., Rio, E., Restagno, F., van Nierop, E., Cantat, I., Langevin, D. & Stone, H. 2010 The role of surface rheology in liquid film formation. Europhys. Lett. 90, 24002.CrossRefGoogle Scholar
Spiegelberg, S.H., Ables, D.C. & McKinley, G.H. 1996 The role of end-effects on measurements of extensional viscosity in filament stretching rheometers. J. Non-Newtonian Fluid Mech. 64 (2), 229–267.CrossRefGoogle Scholar
Tang, Y. & Cheng, S. 2019 The meniscus on the outside of a circular cylinder: From microscopic to macroscopic scales. J. Colloid Interface Sci. 533, 401–408.CrossRefGoogle ScholarPubMed
Tomotika, S. & Taylor, G.I. 1936 Breaking up of a drop of viscous liquid immersed in another viscous fluid which is extending at a uniform rate. Proc. R. Soc. Lond. A 153 (879), 302–318.Google Scholar
Trouton, F.T. 1906 On the coefficient of viscous traction and its relation to that of viscosity. Proc. R. Soc. A 77 (519), 426–440.Google Scholar
Verbeke, K., Formenti, S., Vangosa, F.B., Mitrias, C., Reddy, N.K., Anderson, P.D. & Clasen, C. 2020 Liquid bridge length scale based nondimensional groups for mapping transitions between regimes in capillary break-up experiments. Phys. Rev. Fluids 5, 051901.CrossRefGoogle Scholar
Villermaux, E. 2007 Fragmentation. Annu. Rev. Fluid Mech. 39 (1), 419–446.CrossRefGoogle Scholar
Vincent, L., Duchemin, L. & Le Dizès, S. 2014 a Forced dynamics of a short viscous liquid bridge. J. Fluid Mech. 761, 220–240.CrossRefGoogle Scholar
Vincent, L., Duchemin, L. & Villermaux, E. 2014 b Remnants from fast liquid withdrawal. Phys. Fluids 26 (3), 031701.CrossRefGoogle Scholar
Wylie, J.J., Bradshaw-Hajek, B.H. & Stokes, Y.M. 2016 The evolution of a viscous thread pulled with a prescribed speed. J. Fluid Mech. 795, 380–408.CrossRefGoogle Scholar
Yildirim, O.E. & Basaran, O.A. 2001 Deformation and breakup of stretching bridges of Newtonian and shear-thinning liquids: comparison of one- and two-dimensional models. Chem. Engng Sci. 56 (1), 211–233.CrossRefGoogle Scholar
Zhang, X., Padgett, R.S. & Basaran, O.A. 1996 Nonlinear deformation and breakup of stretching liquid bridges. J. Fluid Mech. 329, 207–245.CrossRefGoogle Scholar
Zheng, H., Liu, S. & Luo, X. 2013 Enhancing angular color uniformity of phosphor-converted white light-emitting diodes by phosphor dip-transfer coating. J. Lightwave Technol. 31 (12), 1987–1993.CrossRefGoogle Scholar
Zhu, X. & Wang, S.-Q. 2013 Mechanisms for different failure modes in startup uniaxial extension: tensile (rupture-like) failure and necking. J. Rheol. 57 (1), 223–248.CrossRefGoogle Scholar
Zhuang, J. & Ju, Y.S. 2015 A combined experimental and numerical modeling study of the deformation and rupture of axisymmetric liquid bridges under coaxial stretching. Langmuir 31 (37), 10173–10182.CrossRefGoogle ScholarPubMed