Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T20:05:20.052Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of flow in a channel with longitudinal grooves

Published online by Cambridge University Press:  25 September 2014

H. V. Moradi  and
J. M. Floryan
H. V. Moradi*
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, N6A 5B9, Canada
J. M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, N6A 5B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

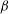The travelling wave instability in a channel with small-amplitude longitudinal grooves of arbitrary shape has been studied. The disturbance velocity field is always three-dimensional with disturbances which connect to the two-dimensional waves in the limit of zero groove amplitude playing the critical role. The presence of grooves destabilizes the flow if the groove wavenumber $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\beta $ is larger than 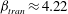$\beta _{tran}\approx 4.22$, but stabilizes the flow for smaller 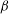$\beta $. It has been found that 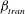$\beta _{tran}$ does not depend on the groove amplitude. The dependence of the critical Reynolds number on the groove amplitude and wavenumber has been determined. Special attention has been paid to the drag-reducing long-wavelength grooves, including the optimal grooves. It has been demonstrated that such grooves slightly increase the critical Reynolds number, i.e. such grooves do not cause an early breakdown into turbulence.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control Flow Control: Instability control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 613 - 648
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asai, M. & Floryan, J. M. 2006 Experiments on the linear instability of flow in a wavy channel. Eur. J. Mech. (B/Fluids) 25, 971–986.CrossRefGoogle Scholar
Bloch, F. 1928 Über die Quantenmechanik der Elektronen in Kristallgittern. Z. Phys. 52, 555–600.Google Scholar
Boiko, A. V., Jung, K. H., Chun, H. H. & Lee, I. 2007 Effect of riblets on the streaky structures excited by free stream tip vortices in boundary layer. J. Mech. Sci. Engng 21, 196–206.Google Scholar
Boiko, A. V., Kozlov, V. V., Syzrantsev, V. V. & Scherbakov, V. A. 1997 Transition control by riblets in swept wing boundary layer with embedded streamwise vortex. Eur. J. Mech. (B/Fluids) 16, 465–482.Google Scholar
Boiko, A. V. & Nechepurenko, Yu. M. 2010 Technique for the numerical analysis of the riblet effect on temporal stability of plane flows. Comput. Math. & Math. Phys. 50, 1055–1070.CrossRefGoogle Scholar
Cabal, A., Szumbarski, J. & Floryan, J. M. 2001 Numerical simulation of flows over corrugated walls. Comput. Fluids 30, 753–776.CrossRefGoogle Scholar
Cabal, T., Szumbarski, J. & Floryan, J. M. 2002 Stability of flow in a wavy channel. J. Fluid Mech. 457, 191–212.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 2006 Spectral Methods. Fundamentals in Single Domains. Springer.Google Scholar
Coddington, E. A. & Levinson, N. 1965 Theory of Ordinary Differential Equations. McGraw-Hill.Google Scholar
Darcy, H. 1857 Recherches Expérimentales Relatives au Mouvement de l’eau Dans les Tuyaux. Mallet-Bachelier.Google Scholar
Dean, B. & Bhushan, B. 2010 Shark-skin surfaces for fluid-drag reduction in turbulent flow: a review. Phil. Trans. R. Soc. A 368, 4775–4806.CrossRefGoogle ScholarPubMed
Denissen, N. A. & White, E. B. 2009 Continuous spectrum analysis of roughness-induced transient growth. Phys. Fluids 21, 114115.Google Scholar
Ehrenstein, U. 1996 On the linear stability of channel flow over riblets. Phys. Fluids 8, 3194–3196.CrossRefGoogle Scholar
Floryan, J. M. 1997 Stability of wall-bounded shear layers in the presence of simulated distributed surface roughness. J. Fluid Mech. 335, 29–55.Google Scholar
Floryan, J. M. 2002 Centrifugal instability of Couette flow over a wavy-wall. Phys. Fluids 14, 312–322.Google Scholar
Floryan, J. M. 2003 Vortex instability in a diverging–converging channel. J. Fluid Mech. 482, 17–50.Google Scholar
Floryan, J. M. 2005 Two-dimensional instability of flow in a rough channel. Phys. Fluids 17, 044101.Google Scholar
Floryan, J. M. 2007 Three-dimensional instabilities of laminar flow in a rough channel and the concept of hydraulically smooth wall. Eur. J. Mech. (B/Fluids) 26, 305–329.Google Scholar
Floryan, J. M. & Asai, M. 2011 On the transition between distributed and isolated surface roughness and its effect on the stability of channel flow. Phys. Fluids 23, 104101.Google Scholar
Floryan, J. M. & Floryan, C. 2010 Travelling wave instability in a diverging–converging channel. Fluid Dyn. Res. 42, 025509.CrossRefGoogle Scholar
Gibbs, J. W. 1898 Fourier’s series. Nature 59 (1522), 200.Google Scholar
Gibbs, J. W. 1899 Fourier’s series. Nature 59 (1539), 606.CrossRefGoogle Scholar
Grek, G. R., Kozlov, V. V. & Titarenko, S. V. 1996 An experimental study of the influence of riblets on transition. J. Fluid Mech. 315, 31–45.Google Scholar
Hagen, G. 1854 Uber den Einfluss der Temperatur auf die Bewegung des Wasser in Röhren. (Mathematische Abhandhmgen) , pp. 17–98. Akademie der Wissenschaften zu Berlin.Google Scholar
Herbert, T. 1977 Finite amplitude stability of plane parallel flows. AGARD Conference Proceedings 224, 3.1–3.10.Google Scholar
Herwig, H., Gloss, D. & Wenterodt, T. 2008 A new approach to understanding and modelling the influence of wall roughness on friction factors for pipe and channel flows. J. Fluid Mech. 613, 35–53.Google Scholar
Husain, S. Z. & Floryan, J. M. 2010 Spectrally-accurate algorithm for moving boundary problems for the Navier–Stokes equations. J. Comput. Phys. 229, 2287–2313.CrossRefGoogle Scholar
Husain, S. Z., Floryan, J. M. & Szumbarski, J. 2009 Over-determined formulation of the immersed boundary condition method. Comput. Meth. Appl. Mech. Engng 199, 94–112.Google Scholar
Inasawa, A., Floryan, J. M. & Asai, M. 2014 Flow recovery downstream from a surface protuberance. Theor. Comput. Fluid Dyn. 28, 427–447.Google Scholar
Jimenez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Jin, Y. & Herwig, H. 2014 Turbulent flow and heat transfer in channels with shark skin surfaces: entropy generation and its physical significance. Intl J. Heat Mass Transfer 70, 10–22.Google Scholar
Klamp, S., Meinke, M. & Schröder, W. 2010 Numerical simulation of riblet controlled spatial transition in a zero-pressure-gradient boundary layer. Flow Turbul. Combust. 85, 57–71.Google Scholar
Luchini, P. & Trombetta, G. 1995 Effects of riblets upon flow stability. Appl. Sci. Res. 54, 313–321.Google Scholar
Mohammadi, A. & Floryan, J. M. 2012 Spectral algorithm for the analysis of flows in grooved channels. Intl J. Numer. Meth. Fluids 69, 606–638.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J. M. 2013a Groove optimization for drag reduction. Phys. Fluids 25, 113601.Google Scholar
Mohammadi, A. & Floryan, J. M. 2013b Pressure losses in grooved channels. J. Fluid Mech. 725, 23–54.Google Scholar
Moody, L. F. & Princeton, N. J. 1944 Friction factors for pipe flow. Trans. ASME 66, 671–684.Google Scholar
Moradi, H. V. & Floryan, J. M. 2012 Algorithm for analysis of flows in ribbed annuli. Intl J. Numer. Meth. Fluids 68, 805–838.Google Scholar
Moradi, H. & Floryan, J. M. 2013a Flows in annuli with longitudinal grooves. J. Fluid Mech. 716, 280–315.CrossRefGoogle Scholar
Moradi, H. & Floryan, J. M. 2013b Maximization of heat transfer across micro-channels. Intl J. Heat Mass Transfer 66, 517–530.Google Scholar
Morkovin, M. V. 1990 On roughness-induced transition: facts, views and speculations. In Instability and Transition (ed. Hussaini, M. Y. & Voigt, R. G.), ICASE/NASA LARC Series, vol. 1, pp. 281–295. Springer, New York.Google Scholar
Orszag, S. A. 1971 Accurate solutions of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–704.Google Scholar
Orszag, S. A. & Patera, A. T. 1983 Secondary instability of wall-bounded shear flows. J. Fluid Mech. 128, 347–385.Google Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the wall of resistance in parallel channels. Phil. Trans. R. Soc. Lond. 174, 935–982.Google Scholar
Rothenflue, J. A. & King, P. I. 1995 Vortex development over flat plate riblets in a transitioning boundary layer. AIAA J. 33, 1525–1526.Google Scholar
Saad, Y. 2003 Iterative Methods for Sparse Linear Systems. SIAM.Google Scholar
Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Squire, H. B. 1933 On the stability of three-dimensional distribution of viscous fluid between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
Szumbarski, J. 2007 Instability of viscous incompressible flow in a channel with transversely corrugated walls. J. Theor. Appl. Mech. 45, 659–683.Google Scholar
Szumbarski, J. & Floryan, J. M. 1999 A direct spectral method for determination of flows over corrugated boundaries. J. Comput. Phys. 153, 378–402.Google Scholar
Szumbarski, J. & Floryan, J. M. 2006 Transient disturbance growth in a corrugated channel. J. Fluid Mech. 568, 243–272.CrossRefGoogle Scholar
Walsh, M. J. 1983 Riblets as a viscous drag reduction technique. AIAA J. 21, 485–486.Google Scholar
White, E. B., Rice, J. M. & Ergin, F. G. 2005 Receptivity of stationary transient disturbances to surface roughness. Phys. Fluids 17, 064109.Google Scholar
Wilbraham, H. 1848 On a certain periodic function. Cambridge Dublin Math. J. 3, 198–201.Google Scholar