Article contents
The spin-up of a linearly stratified fluid in a sliced, circular cylinder
Published online by Cambridge University Press: 30 September 2016
Abstract
A linearly stratified fluid contained in a circular cylinder with a linearly sloped base, whose axis is aligned with the rotation axis, is spun-up from a rotation rate 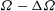 $\unicode[STIX]{x1D6FA}-\unicode[STIX]{x0394}\unicode[STIX]{x1D6FA}$ to
$\unicode[STIX]{x1D6FA}-\unicode[STIX]{x0394}\unicode[STIX]{x1D6FA}$ to  $\unicode[STIX]{x1D6FA}$ (with
$\unicode[STIX]{x1D6FA}$ (with 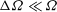 $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FA}\ll \unicode[STIX]{x1D6FA}$) by Rossby waves propagating across the container. Experimental results presented here, however, show that if the Burger number
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FA}\ll \unicode[STIX]{x1D6FA}$) by Rossby waves propagating across the container. Experimental results presented here, however, show that if the Burger number 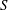 $S$ is not small, then that spin-up looks quite different from that reported by Pedlosky & Greenspan (J. Fluid Mech., vol. 27, 1967, pp. 291–304) for
$S$ is not small, then that spin-up looks quite different from that reported by Pedlosky & Greenspan (J. Fluid Mech., vol. 27, 1967, pp. 291–304) for 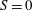 $S=0$. That is particularly so if the Burger number is large, since the Rossby waves are then confined to a region of height
$S=0$. That is particularly so if the Burger number is large, since the Rossby waves are then confined to a region of height 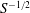 $S^{-1/2}$ above the sloped base. Axial vortices, ubiquitous features even at tiny Rossby numbers of spin-up in containers with vertical corners (see van Heijst et al.Phys. Fluids A, vol. 2, 1990, pp. 150–159 and Munro & Foster Phys. Fluids, vol. 26, 2014, 026603, for example), are less prominent here, forming at locations that are not obvious a priori, but in the ‘western half’ of the container only, and confined to the bottom
$S^{-1/2}$ above the sloped base. Axial vortices, ubiquitous features even at tiny Rossby numbers of spin-up in containers with vertical corners (see van Heijst et al.Phys. Fluids A, vol. 2, 1990, pp. 150–159 and Munro & Foster Phys. Fluids, vol. 26, 2014, 026603, for example), are less prominent here, forming at locations that are not obvious a priori, but in the ‘western half’ of the container only, and confined to the bottom  $S^{-1/2}$ region. Both decay rates from friction at top and bottom walls and the propagation speed of the waves are found to increase with
$S^{-1/2}$ region. Both decay rates from friction at top and bottom walls and the propagation speed of the waves are found to increase with 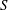 $S$ as well. An asymptotic theory for Rossby numbers that are not too large shows good agreement with many features seen in the experiments. The full frequency spectrum and decay rates for these waves are discussed, again for large
$S$ as well. An asymptotic theory for Rossby numbers that are not too large shows good agreement with many features seen in the experiments. The full frequency spectrum and decay rates for these waves are discussed, again for large 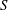 $S$, and vertical vortices are found to occur only for Rossby numbers comparable to
$S$, and vertical vortices are found to occur only for Rossby numbers comparable to 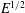 $E^{1/2}$, where
$E^{1/2}$, where  $E$ is the Ekman number. Symmetry anomalies in the observations are determined by analysis to be due to second-order corrections to the lower-wall boundary condition.
$E$ is the Ekman number. Symmetry anomalies in the observations are determined by analysis to be due to second-order corrections to the lower-wall boundary condition.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 2
- Cited by



