Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wu, Xuesong
and
Zhuang, Xiuling
2016.
Nonlinear dynamics of large-scale coherent structures in turbulent free shear layers.
Journal of Fluid Mechanics,
Vol. 787,
Issue. ,
p.
396.
Wu, Xuesong
2019.
Nonlinear Theories for Shear Flow Instabilities: Physical Insights and Practical Implications.
Annual Review of Fluid Mechanics,
Vol. 51,
Issue. 1,
p.
451.
Long, Yanguang
Wang, Jiangsheng
and
Wang, Jinjun
2020.
Vortices evolution in the flow over a sharp leading edge at low Reynolds number.
Experimental Thermal and Fluid Science,
Vol. 112,
Issue. ,
p.
109987.
Zhang, Zhongyu
and
Wu, Xuesong
2020.
Nonlinear evolution and acoustic radiation of coherent structures in subsonic turbulent free shear layers.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Mikhaylov, Kirill
and
Wu, Xuesong
2020.
Nonlinear evolution of interacting sinuous and varicose modes in plane wakes and jets: Quasi-periodic structures.
Physics of Fluids,
Vol. 32,
Issue. 6,
Zhang, Yongming
Zhou, Wenqiang
and
Chen, Xiangzhen
2020.
An investigation on the disturbance evolution and the transition by resonant-triad interactions with a side-frequency disturbance in a boundary layer.
Physics of Fluids,
Vol. 32,
Issue. 7,
Zhang, Zhongyu
and
Wu, Xuesong
2022.
Nonlinear evolution and low-frequency acoustic radiation of ring-mode coherent structures on subsonic turbulent circular jets.
Journal of Fluid Mechanics,
Vol. 940,
Issue. ,
Zhang, Zhongyu
and
Wu, Xuesong
2022.
IUTAM Laminar-Turbulent Transition.
Vol. 38,
Issue. ,
p.
137.
Izawa, Seiichiro
Oku, Tatsuya
Nishio, Yu
and
Fukunishi, Yu
2022.
Onset of nonlinearity in a two-dimensional thin shear layer.
Fluid Dynamics Research,
Vol. 54,
Issue. 2,
p.
025503.
Zhang, Zhongyu
and
Wu, Xuesong
2023.
Nonlinear dynamics and acoustic radiation of coherent structures consisting of multiple ring–helical modes in the near-nozzle region of a subsonic turbulent circular jet.
Journal of Fluid Mechanics,
Vol. 973,
Issue. ,
Xu, Jiakuan
Liu, Jianxin
Zhang, Zhongyu
and
Wu, Xuesong
2023.
Spatial–temporal transformation for primary and secondary instabilities in weakly non-parallel shear flows.
Journal of Fluid Mechanics,
Vol. 959,
Issue. ,
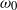 and
and 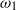 , components with the combination frequencies
, components with the combination frequencies 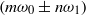 (
(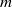 and
and  being integers) develop to a significant level thereby causing flow randomization. This spectral broadening process is investigated theoretically for the case where the frequency difference
being integers) develop to a significant level thereby causing flow randomization. This spectral broadening process is investigated theoretically for the case where the frequency difference 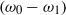 is small, so that the perturbation can be treated as a modulated wavetrain. A nonlinear evolution system governing the spectral dynamics is derived by using the non-equilibrium nonlinear critical layer approach. The formulation provides an appropriate mathematical description of the physical concepts of sideband instability and amplitude–phase modulation, which were suggested by experimentalists. Numerical solutions of the nonlinear evolution system indicate that the present theory captures measurements and observations rather well.
is small, so that the perturbation can be treated as a modulated wavetrain. A nonlinear evolution system governing the spectral dynamics is derived by using the non-equilibrium nonlinear critical layer approach. The formulation provides an appropriate mathematical description of the physical concepts of sideband instability and amplitude–phase modulation, which were suggested by experimentalists. Numerical solutions of the nonlinear evolution system indicate that the present theory captures measurements and observations rather well.