Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T20:02:29.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatio–temporal analysis of hydrodynamic forces on the particle bed in an oscillatory flow environment

Published online by Cambridge University Press:  20 February 2018

Chaitanya D. Ghodke Open the ORCID record for Chaitanya D. Ghodke [Opens in a new window]  and
Sourabh V. Apte
Chaitanya D. Ghodke
Affiliation:
School of Mechanical, Industrial and Manufacturing Engineering, Oregon State University, Corvallis, OR 97331, USA
Sourabh V. Apte
Affiliation:
School of Mechanical, Industrial and Manufacturing Engineering, Oregon State University, Corvallis, OR 97331, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

A numerical investigation of unsteady hydrodynamic forces on the particle bed in an oscillatory flow environment is performed by means of direct numerical simulations. Statistical descriptions of drag and lift forces for two particle sizes of diameter 372 and 125 in wall units in a very rough turbulent flow regime are reported. Characterization of unsteady forces in terms of spatial distribution, temporal autocorrelation, force spectrum as well as cross-correlations with measurable flow variables is carried out. Based on the concept of impulse, intermittency in the drag and lift forces is also investigated. Temporal correlations show drag and lift to be positively correlated with a time delay that is approximately equal to the Taylor micro-scale related to the drag/lift fluctuations. The force spectra for drag and lift reveal roughly two scaling regions, 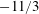$-11/3$ and 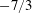$-7/3$; the former typically represents turbulence–mean-shear interactions, whereas the latter indicates dominance of turbulence–turbulence interactions. Particle forces are strongly correlated with streamwise velocity and pressure fluctuations in the near-bed region for both flow cases. In comparison to the large-diameter particle case, the spatial extent of these correlations is 2–3 times larger in homogeneous directions for the small sized particle, a feature that is reminiscent of longer near-bed structures. For both large- and small-particle cases, it is shown that the distributions of drag (lift) fluctuations, in particular, peakedness and long tails, match remarkably well with fourth-order Gram–Charlier distributions of velocity (pressure) fluctuations. Furthermore, it is demonstrated that the intermittency is larger in the case of the lift force compared to that for the drag in both flow cases. Distributions of impulse events are heavily and positively skewed and are well described by a generalized extreme value distribution.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Geophysical and Geological Flows: Sediment transport Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 841 , 25 April 2018 , pp. 167 - 202
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van der A, D., O’Donoghue, T., Davies, A. G. & Ribberink, J. S. 2011 Experimental study of the turbulent boundary layer in acceleration-skewed oscillatory flow. J. Fluid Mech. 684, 251–283.Google Scholar
Amir, M., Nikora, V. I. & Stewart, M. T. 2014 Pressure forces on sediment particles in turbulent open-channel flow: a laboratory study. J. Fluid Mech. 757, 458–497.CrossRefGoogle Scholar
Apte, S. V. & Finn, J. R. 2013 A variable-density fictitious domain method for particulate flows with broad range of particle–fluid density ratios. J. Comput. Phys. 243, 109–129.Google Scholar
Apte, S. V., Mahesh, K. & Moin, P. 2009a Large-eddy simulation of evaporating spray in a coaxial combustor. Proc. Combust. Inst. 32, 2247–2256.Google Scholar
Apte, S. V., Mahesh, K., Moin, P. & Gorokhovski, M. 2009b Stochastic modeling of atomizing spray in a complex swirl injector using large-eddy simulation. Proc. Combust. Inst. 32, 2257–2266.Google Scholar
Apte, S. V., Mahesh, K., Moin, P. & Oefelein, J. C. 2003 Large-eddy simulation of swirling particle-laden flows in a coaxial-jet combustor. Intl J. Multiphase Flow 29 (8), 1311–1331.CrossRefGoogle Scholar
Apte, S. V., Martin, M. & Patankar, N. A. 2008 A numerical method for fully resolved simulation (FRS) of rigid particle–flow interactions in complex flows. J. Comput. Phys. 228 (8), 2712–2738.CrossRefGoogle Scholar
Apte, S. V., Martin, M. & Patankar, N. A. 2009c A numerical method for fully resolved simulation (FRS) of rigid particle–flow interactions in complex flows. J. Comput. Phys. 228 (8), 2712–2738.Google Scholar
Bagnold, R. A. 1966 An approach to the sediment transport problem from general physics. In US Geological Survey Professional Paper, vol. 422, pp. 1–37. https://pubs.er.usgs.gov/publication/pp422I.Google Scholar
Celik, A., Diplas, P. & Dancey, C. 2013 Instantaneous turbulent forces and impulse on a rough bed: implications for initiation of bed material movement. Water Resour. Res. 49, 2213–2227.Google Scholar
Celik, A., Diplas, P. & Dancey, C. 2014 Instantaneous pressure measurements on a spherical grain under threshold conditions. J. Fluid Mech. 741, 60–97.Google Scholar
Celik, A., Diplas, P., Dancey, C. & Valyrakis, M. 2010 Impulse and particle dislodgement under turbulent flow conditions. Phys. Fluids 22, 046601.CrossRefGoogle Scholar
Chan-Braun, C.2012 Turbulent open channel flow, sediment erosion and sediment transport. PhD thesis, Karlsruhe Institute of Technology, Germany.Google Scholar
Chan-Braun, C., Garcia-Villalba, M. & Uhlmann, M. 2011 Force and torque acting on particles in transitionally rough open-channel flow. J. Fluid Mech. 684 (441), 441–474.Google Scholar
Chan-Braun, C., Garcia-Villalba, M. & Uhlmann, M. 2013 Spatial and temporal scales of force and torque acting on wall-mounted spherical particles in open channel flow. Phys. Fluids 25 (7), 075103.CrossRefGoogle Scholar
Chen, D., Chen, C., Tang, F.-E., Stansby, P. & Li, M. 2007 Boundary layer structure of oscillatory open-channel shallow flows over smooth and rough beds. Exp. Fluids 42 (5), 719–736.Google Scholar
Cheng, N. & Chiew, Y. 1998 Pick-up probability for sediment entrainment. J. Hydraul. Engng ASCE 124, 232–235.CrossRefGoogle Scholar
Cheng, N. & Law, A. W.-K. 2003 Fluctuations of turbulent bed shear stress. J. Engng Mech. ASCE 129, 126–130.CrossRefGoogle Scholar
Detert, M., Weitbrecht, V. & Jirka, G. H. 2010 Laboratory measurements on turbulent pressure fluctuations in and above gravel beds. J. Hydraul. Engng ASCE 136, 779–789.Google Scholar
Ding, L. & Zhang, Q.-H. 2010 Lattice Boltzmann simulation to characterize roughness effects of oscillatory boundary layer flow over a rough bed. In Proc. 32nd Conference on Coastal Eng., pp. 1–11.Google Scholar
Diplas, P., Dancey, C. L., Celik, A. O., Valyrakis, M., Greer, K. & Akar, T. 2008 The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 322 (5902), 717–720.CrossRefGoogle ScholarPubMed
Dixen, M., Hatipoglu, F., Sumer, B. M. & Fredsøe, J. 2008 Wave boundary layer over a stone-covered bed. Coast. Engng 55, 1–20.Google Scholar
Dwivedi, A.2010 Mechanics of sediment entrainment. PhD thesis, The University of Auckland.Google Scholar
Dwivedi, A., Melville, B. & Shamseldin, A. Y. 2010 Hydrodynamic forces generated on spherical sediment particle during entrainment. J. Hydraul. Engng ASCE 136, 756–769.Google Scholar
Einstein, H. 1950 The Bed-Load Function for Sediment Transportation in Open Channel Flows. U.S. Department of Agriculture.Google Scholar
Flores, N. & Sleath, J. 1998 Mobile layer in oscillatory sheet flow. J. Geophys. Res. 103.Google Scholar
Fornarelli, F. & Vittori, G. 2009 Oscillatory boundary layer close to a rough wall. Eur. J. Mech. (B/Fluids) 28, 283–295.Google Scholar
Fredsøe, J. & Deigaard, R. 1992 Mechanics of Coastal Sediment Transport. World Scientific.Google Scholar
George, W. K., Beuther, P. D. & Arndt, R. E. 1984 Pressure spectra in turbulent free shear flows. J. Fluid Mech. 148, 148–191.Google Scholar
Ghodke, C. D.2016 DNS study of particle-bed–turbulence interactions in oscillatory flows. PhD thesis, Oregon State University, USA.Google Scholar
Ghodke, C. D. & Apte, S. V.2014 DNS of oscillatory boundary layer over a closely packed layer of sediment particles. In Proc. ASME Fluids Engineering Summer Meeting, Chicago, IL, USA. Paper number: FEDSM2014-21719.Google Scholar
Ghodke, C. D. & Apte, S. V.2016a A numerical investigation of particle-bed–turbulence interactions in oscillatory flows. In Proc. ICMF 9th International Conference on Multiphase Flow, Firenze, Italy.Google Scholar
Ghodke, C. D. & Apte, S. V. 2016b DNS study of particle-bed–turbulence interactions in an oscillatory wall-bounded flow. J. Fluid Mech. 792, 232–251.CrossRefGoogle Scholar
Ghodke, C. D. & Apte, S. V.2016c Particle-resolved DNS to study spatio-temporal correlations of hydrodynamic forces on particle-bed in an oscillatory flow environment. In Proc. ASME Fluids Engineering Summer Meeting, Washington DC, USA. Paper number: FEDSM2016-7761.Google Scholar
Ghodke, C. D. & Apte, S. V.2017 A numerical investigation to study roughness effects in oscillatory flows. In Proc. ASME Fluids Engineering Summer Meeting, Hawaii, USA. Paper number: FEDSM2017-69066.Google Scholar
Ghodke, C. D. & Apte, S. V. 2018 Roughness effects on second-order turbulence statistics in oscillatory flows. Comput. Fluids 162, 160–170.Google Scholar
Ghodke, C. D., Apte, S. V. & Urzay, J.2014a Direct numerical simulations of oscillatory wall-bounded flow over a closely-packed fixed bed of spherical particles. In Proc. Center for Turbulence Research Summer Prog., pp. 47–55.Google Scholar
Ghodke, C. D., Skitka, J. & Apte, S. V. 2014b Characterization of oscillatory boundary layer over a closely packed bed of sediment particles. J. Comput. Multiphase Flows 6 (4), 187–197.Google Scholar
Glowinski, R., Pan, T. W., Hesla, T. I., Joseph, D. D. & Periaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies – application to particulate flow. J. Comput. Phys. 169 (2), 363–426.CrossRefGoogle Scholar
Hofland, B.2005 Rock and roll, turbulence-induced damage to granular bed protections. PhD thesis, Delft University of Technology, Netherlands.Google Scholar
Hofland, B. & Battjes, J. 2006 Probability density function of instantaneous drag forces and shear stresses on a bed. J. Hydraul. Engng ASCE 132, 1169–1175.CrossRefGoogle Scholar
Hofland, B., Battjes, J. & Booij, R. 2005 Measurement of fluctuating pressures on coarse bed material. J. Hydraul. Engng ASCE 131, 770–781.Google Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.CrossRefGoogle Scholar
Jensen, B. L., Sumer, B. M. & Fredsøe, J. 1989 Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 206, 265–297.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jonsson, I. G. & Carlsen, N. A. 1976 Experimental and theoretical investigations in an oscillatory turbulent boundary layer. J. Hydraul Res. 14, 45–60.CrossRefGoogle Scholar
Keiller, D. C. & Sleath, J. F. A. 1976 Velocity measurements close to a rough plate oscillating in its own plane. J. Fluid Mech. 73 (04), 673–691.Google Scholar
Kemp, P. H. & Simons, R. R. 1982 The interaction of waves with a turbulent current: waves propagating against the current. J. Fluid Mech. 130, 73–89.CrossRefGoogle Scholar
Kempe, T., Vowinckel, B. & Fröhlich, J. 2014 On the relevance of collision modeling for interface-resolving simulations of sediment transport in open channel flow. Intl J. Multiphase Flow 58, 214–235.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Krogstad, P.-A., Andersson, H. I., Bakken, O. M. & Ashrafin, A. 2005 An experimental and numerical study of channel flow with rough walls. J. Fluid Mech. 530, 327–352.Google Scholar
Krogstad, P.-A. & Antonia, R. A. 1994 Stucture of turbulent boundary layers on smooth and rough walls. J. Fluid Mech. 277, 1–21.CrossRefGoogle Scholar
Krogstad, P.-A., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.Google Scholar
Krstic, R. V. & Fernando, H. J. S. 2001 The nature of rough-wall oscillatory boundary layers. J. Hydraul Res. 30, 655–666.Google Scholar
Mahesh, K., Constantinescu, G., Apte, S., Iaccarino, G., Ham, F. & Moin, P. 2006 Large-eddy simulation of reacting turbulent flows in complex geometries. Trans. ASME J. Appl. Mech. 73, 374.CrossRefGoogle Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197 (1), 215–240.CrossRefGoogle Scholar
Mazzuoli, M. & Vittori, G. 2016 Transition to turbulence in an oscillatory flow over a rough wall. J. Fluid Mech. 792, 67–97.CrossRefGoogle Scholar
Mingmin, H. & Qiwei, H. 1982 Stochastic model of incipient sediment motion. J. Hydraul. Div. ASCE 108, 211–224.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.Google Scholar
Nelson, J. M., Schmeeckle, M. W., Shreve, R. L. & McLean, S. R.2000 Sediment entrainment and transport in complex flows. In Selected Papers of the Int. Assoc. Hydraulic Research Symp. on River, Coastal and Estuarine Morphodynamics, Genova, Italy.Google Scholar
Nino, Y., Lopez, F. & Garcia, M. 2003 Threshold for particle entrainment into suspension. Sedimentology 50 (2), 247–263.Google Scholar
Papanicolaou, A., Diplas, P., Evaggelopoulos, N. & Fotopoulos, S. 2002 Stochastic incipient motion criterion for spheres under various bed packing conditions. J. Hydraul. Engng ASCE 128, 369–380.Google Scholar
Roma, A. M., Peskin, C. S. & Berger, M. J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153 (2), 509–534.Google Scholar
Rosenthal, G. N. & Sleath, J. F. A. 1986 Measurements of lift in oscillatory flow. J. Fluid Mech. 164, 449–467.Google Scholar
Schmeeckle, M. W., Nelson, J. M. & Shreve, R. L. 2007 Forces on stationary particles in near-bed turbulent flows. J. Geophy. Res. 112, F02003.Google Scholar
Sharma, N. & Patankar, N. A. 2005 A fast computation technique for the direct numerical simulation of rigid particulate flows. J. Comput. Phys. 205 (2), 439–457.Google Scholar
Shields, A.1936 Application of Similarity Principles and Turbulence Research to Bed-Load Movement. California Institute of Technology; translated from German. https://authors.library.caltech.edu/25992/1/Sheilds.pdf.Google Scholar
Sleath, J. F. A. 1987 Turbulent oscillatory flows over rough beds. J. Fluid Mech. 182, 369–409.Google Scholar
Sleath, J. 1995 Sediment transport by waves and currents. J. Geophys. Res. 100.Google Scholar
Sleath, J. 1999 Conditions for plug formation in oscillatory flow. Cont. Shelf Res. 13.Google Scholar
Valyrakis, M., Diplas, P., Dancey, C., Greer, K. & Celik, A. 2010 Role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res. 115.Google Scholar
Van Rijn, L. C. 1984 Sediment pick-up functions. J. Hydraul. Engng ASCE 110 (10), 1494–1502.CrossRefGoogle Scholar
Welch, P. D. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73.Google Scholar
Wu, F.-C. & Chou, Y.-J. 2003 Rolling and lifting probabilities for sediment entrainment. J. Hydraul. Engng ASCE 129, 110–119.Google Scholar
Wu, F.-C. & Kuo-Hsin, Y. 2004 Entrainment probabilities of mixed-size sediment incorporating near-bed coherent flow structures. J. Hydraul. Engng ASCE 130, 1187–1197.Google Scholar
Wu, F.-C. & Lin, Y.-C. 2002 Pickup probability of sediment under log-normal velocity distribution. J. Hydraul. Engng ASCE 128, 438–442.Google Scholar
Yuan, J. & Piomelli, U. 2014 Roughness effects on the Reynolds stress budgets in near-wall turbulence. J. Fluid Mech. 760, R1.CrossRefGoogle Scholar