Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T14:45:17.949Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatial variations of magnetic permeability as a source of dynamo action

Published online by Cambridge University Press:  19 June 2013

B. Gallet ,
F. Pétrélis  and
S. Fauve
B. Gallet*
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure CNRS UMR8550, 24 rue Lhomond, F-75005 Paris, France
F. Pétrélis
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure CNRS UMR8550, 24 rue Lhomond, F-75005 Paris, France
S. Fauve
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure CNRS UMR8550, 24 rue Lhomond, F-75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate dynamo action for a parallel flow of an electrically conducting fluid located over a boundary with spatially varying magnetic permeability. We first compute the dynamo threshold numerically. Then we perform an asymptotic expansion in the limit of small permeability modulation, which gives accurate results even for moderate modulation. We present in detail the mechanism at work for this dynamo. 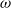It is an interplay between shear (an $\omega $-effect) and a new conversion mechanism that originates from the non-uniform magnetic boundary. We illustrate how a similar mechanism leads to dynamo action in the case of spatially modulated electrical conductivity, a problem studied by Busse & Wicht (Geophys. Astrophys. Fluid Dyn., vol. 64, 1992, pp. 135–144). Finally, we discuss the relevance of this effect to experimental dynamos and present ways to increase the dynamo efficiency and reduce the instability threshold.

JFM classification

Nonlinear Dynamical Systems: Bifurcation MHD and Electrohydrodynamics: Dynamo theory MHD and Electrohydrodynamics: MHD and Electrohydrodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 727 , 25 July 2013 , pp. 161 - 190
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Busse, F. H. & Wicht, J. 1992 A simple dynamo caused by conductivity variations. Geophys. Astrophys. Fluid Dyn. 64, 135–144.Google Scholar
Cowling, T. G. 1933 The magnetic field of sunspots. Mon. Not. R. Astron. Soc. 94, 39–48.Google Scholar
Gallet, B., Pétrélis, F. & Fauve, S. 2012 Dynamo action due to spatially dependent magnetic permeability. Europhys. Lett. 97, 69001.Google Scholar
Giesecke, A., Stefani, F. & Gerbeth, G. 2010 Role of soft-iron impellers on the mode selection in the von Kármán sodium dynamo experiment. Phys. Rev. Lett. 104, 044503.Google Scholar
Gilbert, A. D. 1988 Fast dynamo action in the Ponomarenko dynamo. Geophys. Astrophys. Fluid Dyn. 44, 241–258.CrossRefGoogle Scholar
Gissinger, C. 2009 A numerical model of the VKS experiment. Europhys. Lett. 87, 39002.Google Scholar
Guckenheimer, J. & Holmes, P. 1986 Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer.Google Scholar
Ivers, D. J. & James, R. W. 1984 Axisymmetric antidynamo theorems in compressible non-uniform conducting fluids. Phil. Trans R. Soc. Lond. A 312, 179–218.Google Scholar
Knobloch, E. & Silber, M. 1990 Travelling wave convection in a rotating layer. Geophys. Astrophys. Fluid Dyn. 51, 195–209.CrossRefGoogle Scholar
Larmor, J. 1919 How could a rotating body such as the sun become a magnet?. In Rep. 87th Meeting Brit. Assoc. Adv. Sci., Bornemouth, Sept. 9–13, pp. 159–160. John Murray.Google Scholar
Laure, P., Chossat, P. & Daviaud, F. 2001 Generation of magnetic field in the Couette–Taylor system. In Dynamo and Dynamics, a Mathematical Challenge (ed. Chossat, P., Ambruster, D. & Oprea, I.). pp. 17–24. Kluwer.Google Scholar
Lortz, D. 1968 Impossibility of dynamos with certain symmetries. Phys. Fluids 11, 913–915.CrossRefGoogle Scholar
Matthews, P. C. 1999 Dynamo action in simple convective flows. Proc. R. Soc. Lond. A 455, 1829–1840.CrossRefGoogle Scholar
Monchaux, R., Berhanu, M., Aumaître, S., Chiffaudel, A., Daviaud, F., Dubrulle, B., Ravelet, F., Fauve, S., Mordant, N., Pétrélis, F., Bourgoin, M., Odier, P., Pinton, J.-F., Plihon, N. & Volk, R. 2009 The von Kármán sodium experiment: turbulent dynamical dynamos. Phys. Fluids 21, 035108.Google Scholar
Pétrélis, F., Mordant, N. & Fauve, S. 2007 On the magnetic fields generated by experimental dynamos. Geophys. Astrophys. Fluid Dyn. 101, 289–323.Google Scholar
Plunian, F. & Radler, K. H. 2002 Subharmonic dynamo action in the Roberts flow. Geophys. Astrophys. Fluid Dyn. 96, 115–133.CrossRefGoogle Scholar
Siemens, C. W. 1867 On the conversion of dynamical into electrical force without the aid of permanent magnetism. Proc. R. Soc. Lond. 15, 367–369.Google Scholar
Stefani, F., Xu, M., Gerbeth, G., Ravelet, F., Chiffaudel, A., Daviaud, F. & Léorat, J. 2006 Ambivalent effects of added lid layers on steady kinematic dynamos in cylindrical geometry: application to the VKS experiment. Eur. J. Mech. B/Fluids 25, 894–908.Google Scholar
Tilgner, A. & Busse, F. H. 1995 Subharmonic dynamo action of fluid motions with two-dimensional periodicity. Proc. R. Soc. Lond, A 448, 237–244.Google Scholar
Wicht, J. & Busse, F. H. 1994 Dynamo action induced by lateral variation of conductivity. In Solar and Planetary Dynamos (ed. Proctor, M. R. E., Matthews, P. C. & Rucklidge, A. M.), pp. 329–338. Cambridge University Press.Google Scholar
Zel’dovich, Ya. B. 1957 The magnetic field in the two-dimensional motion of a conducting turbulent fluid. Sov. Phys. JETP 4, 460–462.Google Scholar