Article contents
Spatial organisation of velocity structures for large passive scalar gradients
Published online by Cambridge University Press: 06 January 2020
Abstract
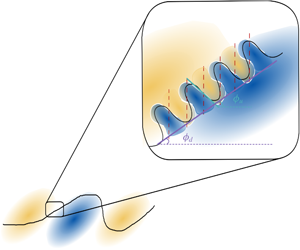
Velocity structures associated with large streamwise density gradients in an incompressible turbulent boundary layer (with air as the working fluid,  $Pr=0.71$) are analysed experimentally using planar image velocimetry and aero-optic measurements. The resulting flow topologies for the velocity fluctuations associated with large negative and positive density gradients are in excellent agreement with results for coolings and heatings in time, respectively (Antonia & Fulachier, J. Fluid Mech., vol. 198, 1989, pp. 429–451). The current results are complimentary to those from Saxton-Fox et al. (AIAA J., vol. 57 (7), 2019, pp. 2828–2839), on the signature of the vertical velocity structures associated with large density gradients. In the present work, these structures are shown to exhibit a sign change, consistent with the scalar gradient, and are localised in the wall-normal direction with an average height of approximately
$Pr=0.71$) are analysed experimentally using planar image velocimetry and aero-optic measurements. The resulting flow topologies for the velocity fluctuations associated with large negative and positive density gradients are in excellent agreement with results for coolings and heatings in time, respectively (Antonia & Fulachier, J. Fluid Mech., vol. 198, 1989, pp. 429–451). The current results are complimentary to those from Saxton-Fox et al. (AIAA J., vol. 57 (7), 2019, pp. 2828–2839), on the signature of the vertical velocity structures associated with large density gradients. In the present work, these structures are shown to exhibit a sign change, consistent with the scalar gradient, and are localised in the wall-normal direction with an average height of approximately  $0.1\unicode[STIX]{x1D6FF}$, almost constant for increasing distance from the wall. The corresponding small-scale streamwise fluctuations also exhibit a consistent sign change, which is found to originate, on average, from upstream leaning structures. The emerging picture for the velocity field is then that of a multiscale phenomenon, where small-scale structures, responsible for large optical aberrations, are superimposed on the back of large-scale bulge-like structures that are known to populate the outer layers. The proposed conceptual model is consistent with early ideas of ‘typical’ eddies (Falco, Phys. Fluids, vol. 20 (10), 1977, pp. S124–S132), the hairpin vortex model and associated shear layers (Adrian et al., J. Fluid Mech., vol. 422, 2000, pp.1–54), as well as with notions of multiscale velocity organisation in shear layers (Klewicki & Hirschi, Phys. Fluids, vol. 16 (11), 2004, pp. 4163–4176; Saxton-Fox et al. 2019), and it provides new insight into the geometry of the small-scale velocity structures.
$0.1\unicode[STIX]{x1D6FF}$, almost constant for increasing distance from the wall. The corresponding small-scale streamwise fluctuations also exhibit a consistent sign change, which is found to originate, on average, from upstream leaning structures. The emerging picture for the velocity field is then that of a multiscale phenomenon, where small-scale structures, responsible for large optical aberrations, are superimposed on the back of large-scale bulge-like structures that are known to populate the outer layers. The proposed conceptual model is consistent with early ideas of ‘typical’ eddies (Falco, Phys. Fluids, vol. 20 (10), 1977, pp. S124–S132), the hairpin vortex model and associated shear layers (Adrian et al., J. Fluid Mech., vol. 422, 2000, pp.1–54), as well as with notions of multiscale velocity organisation in shear layers (Klewicki & Hirschi, Phys. Fluids, vol. 16 (11), 2004, pp. 4163–4176; Saxton-Fox et al. 2019), and it provides new insight into the geometry of the small-scale velocity structures.
- Type
- JFM Papers
- Information
- Copyright
- © 2020 Cambridge University Press
References
- 3
- Cited by


