No CrossRef data available.
Published online by Cambridge University Press: 20 January 2025
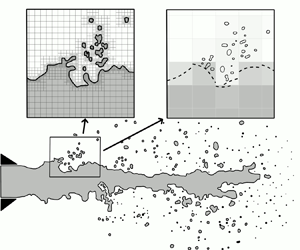
In this contribution, we develop a versatile formalism to derive unified two-phase models describing both the separated and disperse regimes as introduced by Loison et al. (Intl J. Multiphase Flow, vol. 177, 2024, 104857). It relies on the stationary action principle and interface geometric variables. This contribution provides a novel method to derive small-scale models for the dynamics of the interface geometry. They are introduced here on a simplified case where all the scales and phases have the same velocity and that does not take into account large-scale capillary forces. The derivation tools yield a proper mathematical framework through hyperbolicity and signed entropy evolution. The formalism encompasses a hierarchy of small-scale reduced-order models based on a statistical description at a mesoscopic kinetic level and is naturally able to include the description of a disperse phase with polydispersity in size. This hierarchy includes both a cloud of spherical droplets and non-spherical droplets experiencing a dynamical behaviour through incompressible oscillations. The associated small-scale variables are moments of a number density function resulting from the geometric method of moments (GeoMOM). This method selects moments as small-scale geometric variables compatible with the structure and dynamics of the interface; they are defined independently of the flow topology and, therefore, this model allows the coupling of the two-scale flow with an inter-scale transfer. It is shown, in particular, that the resulting dynamics provides partial closures for the interface area density equation obtained from the averaging approach.