Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T10:29:37.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Slipping motion of large neutrally buoyant particles in turbulence

Published online by Cambridge University Press:  15 October 2013

Mamadou Cisse ,
Holger Homann  and
Jérémie Bec
Mamadou Cisse
Affiliation:
Laboratoire Lagrange UMR 7293, Université de Nice-Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, Bd. de l’Observatoire, 06300 Nice, France
Holger Homann
Affiliation:
Laboratoire Lagrange UMR 7293, Université de Nice-Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, Bd. de l’Observatoire, 06300 Nice, France
Jérémie Bec*
Affiliation:
Laboratoire Lagrange UMR 7293, Université de Nice-Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, Bd. de l’Observatoire, 06300 Nice, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations are used to investigate the individual dynamics of large spherical particles suspended in a developed homogeneous turbulent flow. A definition of the direction of the particle motion relative to the surrounding flow is introduced and used to construct the mean fluid velocity profile around the particle. This leads to an estimate of the particle slipping velocity and its associated Reynolds number. The flow modifications due to the particle are then studied. The particle is responsible for a shadowing effect that occurs in the wake up to distances of the order of its diameter: the particle calms turbulent fluctuations and reduces the energy dissipation rate compared to its average value in the bulk. Dimensional arguments are presented to draw an analogy between particle effects on turbulence and wall flows. 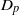Evidence is obtained for the presence of a logarithmic sublayer at distances between the thickness of the viscous boundary layer and the particle diameter ${D}_{p} $. Finally, asymptotic arguments are used to relate the viscous sublayer quantities to the particle size and the properties of the outer turbulence. It is shown in particular that the skin-friction Reynolds number behaves as $R{e}_{\tau } \propto {({D}_{p} / \eta )}^{4/ 3} $.

JFM classification

Boundary Layers: Boundary Layers Turbulent Flows: Turbulent Flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 735 , 25 November 2013 , R1
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Bellani, G., Byron, M. L., Collignon, A. G., Meyer, C. R. & Variano, E. A. 2012 Shape effects on turbulent modulation by large nearly neutrally buoyant particles. J. Fluid Mech. 712, 41–60.Google Scholar
Bellani, G. & Variano, E. A. 2012 Slip velocity of large neutrally buoyant particles in turbulent flows. New J. Phys. 14 (12), 125009.Google Scholar
Garcia-Villalba, M., Kidanemariam, A. G. & Uhlmann, M. 2012 DNS of vertical plane channel flow with finite-size particles: Voronoi analysis, acceleration statistics and particle-conditioned averaging. Intl J. Multiphase Flow 46, 54–74.Google Scholar
Gatignol, R. 1983 The Faxén formulae for a rigid sphere in an unsteady non-uniform Stokes flow. J. Méc. Théor. Appl. 1, 143–160.Google Scholar
Homann, H. & Bec, J. 2010 Finite-size effects in the dynamics of neutrally buoyant particles in turbulent flow. J. Fluid Mech. 651, 81–91.Google Scholar
Homann, H., Bec, J. & Grauer, R. 2013 Effect of turbulent fluctuations on the drag and lift forces on a towed sphere and its boundary layer. J. Fluid Mech. 721, 155–179.Google Scholar
Kajishima, T. 2004 Influence of particle rotation on the interaction between particle clusters and particle-induced turbulence. Intl J. Heat Fluid Flow 25, 721–728.Google Scholar
Khalitov, D. A. & Longmire, E. K. 2002 Simultaneous two-phase PIV by two-parameter phase discrimination. Exp. Fluids 32, 252–268.Google Scholar
Kidanemariam, A., Chan-Braun, C., Doychev, T. & Uhlmann, M. 2013 Direct numerical simulation of horizontal open channel flow with finite-size, heavy particles at low solid volume fraction. New J. Phys. 15, 025031.CrossRefGoogle Scholar
Klein, S., Gibert, M., Bérut, A. & Bodenschatz, E. 2012 Simultaneous 3d measurement of the translation and rotation of finite size particles and the flow field in a fully developed turbulent water flow. Meas. Sci. Technol. 24, 024006.Google Scholar
Legendre, D., Merle, A. & Magnaudet, J. 2006 Wake of a spherical bubble or a solid sphere set fixed in a turbulent environment. Phys. Fluids 18, 048102.CrossRefGoogle Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length scale size. J. Fluid Mech. 650, 5–55.CrossRefGoogle Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
Naso, A. & Prosperetti, A. 2010 The interaction between a solid particle and a turbulent flow. New J. Phys. 12, 033040.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Qureshi, N., Bourgoin, M., Baudet, C., Cartellier, A. & Gagne, Y. 2007 Turbulent transport of material particles: an experimental study of finite size effects. Phys. Rev. Lett. 99, 184502.Google Scholar
Tanaka, T. & Eaton, J. 2010 Sub-Kolmogorov resolution particle image velocimetry measurements of particle–laden forced turbulence. J. Fluid Mech. 643, 177–206.CrossRefGoogle Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Volk, R., Calzavarini, E., Lévêque, E. & Pinton, J.-F. 2011 Dynamics of inertial particles in a turbulent von Kármán flow. J. Fluid Mech. 668, 223–235.Google Scholar
Xu, H. & Bodenschatz, E. 2008 Motion of inertial particles with sizes larger than Kolmogorov scales in turbulent flows. Physica D 237, 2095–2100.CrossRefGoogle Scholar
Zeng, L., Balachandar, S. & Najjar, F. M. 2010 Wake response of a stationary finite-sized particle in a turbulent channel flow. Intl J. Multiphase Flow 36, 406–422.CrossRefGoogle Scholar
Zimmermann, R., Gasteuil, Y., Bourgoin, M., Volk, R., Pumir, A. & Pinton, J.-F. 2011 Rotational intermittency and turbulence induced lift experienced by large particles in a turbulent flow. Phys. Rev. Lett. 106, 154501.Google Scholar