Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T16:02:57.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Simply-connected vortex-patch shallow-water quasi-equilibria

Published online by Cambridge University Press:  05 March 2014

H. Płotka  and
D. G. Dritschel
H. Płotka*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews, Fife KY16 9SS, UK
D. G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews, Fife KY16 9SS, UK
*
†Present address: Department of Earth Sciences, ETH Zürich, 8092 Zürich, Switzerland. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the form, properties, stability and evolution of simply-connected vortex-patch relative quasi-equilibria in the single-layer 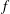$f$-plane shallow-water model of geophysical fluid dynamics. We examine the effects of the size, shape and strength of vortices in this system, represented by three distinct parameters completely describing the families of the quasi-equilibria. Namely, these are the ratio 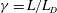$\gamma = L/L_D$ between the horizontal size of the vortices and the Rossby deformation length; the aspect ratio 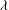$\lambda $ between the minor to major axes of the vortex; and a potential vorticity (PV)-based Rossby number 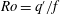$\mathit{Ro}= q^{\prime }/f$, the ratio of the PV anomaly 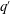$q^{\prime }$ within the vortex to the Coriolis frequency 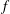$f$. By defining an appropriate steadiness parameter, we find that the quasi-equilibria remain steady for long times, enabling us to determine the boundary of stability 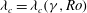$\lambda _c=\lambda _c(\gamma ,\mathit{Ro})$, for 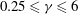$0.25 \leq \gamma \leq 6$ and 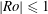$\delimiter "026A30C \mathit{Ro}\delimiter "026A30C \leq 1$. By calling two states which share 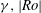$\gamma ,\delimiter "026A30C \mathit{Ro}\delimiter "026A30C $ and 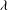$\lambda $ ‘equivalent’, we find a clear asymmetry in the stability of cyclonic (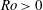$\mathit{Ro}> 0$) and anticyclonic (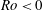$\mathit{Ro}<0$) equilibria, with cyclones being able to sustain greater deformations than anticyclones before experiencing an instability. We find that ageostrophic motions stabilise cyclones and destabilise anticyclones. Both types of vortices undergo the same main types of unstable evolution, albeit in different ranges of the parameter space, (a) vacillations for large-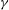$\gamma $, large-$\mathit{Ro}$ states, (b) filamentation for small-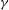$\gamma $ states and (c) vortex splitting, asymmetric for intermediate-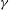$\gamma $ and symmetric for large-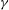$\gamma $ states.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Shallow water flows Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 743 , 25 March 2014 , pp. 481 - 502
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arai, M. & Yamagata, T. 1994 Asymmetric evolution of eddies in rotating shallow water. Chaos 4 (1), 163–175.Google Scholar
Aristegui, J., Sangrá, P., Hernandez-León, S., Canton, M., Hernández-Guerra, A. & Kerling, J. L. 1994 Island-induced eddies in the Canary islands. Deep-Sea Res. 41, 1509–1525.CrossRefGoogle Scholar
Baey, J.-M. & Carton, X. 2002 Vortex multipoles in two-layer rotating shallow-water flows. J. Fluid Mech. 460, 151–175.Google Scholar
Carton, X. 2001 Hydrodynamical modelling of oceanic vortices. Surv. Geophys. 22, 179–263.Google Scholar
Cushman-Roisin, B. 1987 Exact analytical solutions for the elliptical vortices of the shallow-water equations. Tellus A 39, 235–244.Google Scholar
Cushman-Roisin, B., Heil, W. H. & Nof, D. 1985 Oscillations and rotations of elliptical warm-core rings. J. Geophys. Res. 90 (C6), 11756–11764.Google Scholar
Cushman-Roisin, B. & Tang, B. 1990 Geostrophic turbulence and emergence of eddies beyond the radius of deformation. J. Phys. Oceanogr. 20, 97–113.Google Scholar
Deem, G. S. & Zabusky, N. J. 1978a Stationary ‘V-states’, interactions, recurrence, and breaking. In Solitons in Action (ed. Lonngren, K. & Scott, A.), pp. 277–293. Academic Press.Google Scholar
Deem, G. S. & Zabusky, N. J. 1978b Vortex waves: stationary ‘V-states’, interactions, recurrence, and breaking. Phys. Rev. Lett. 40, 859–862.Google Scholar
Dritschel, D. G. 1985 The stability and energetics of corotating uniform vortices. J. Fluid Mech. 157, 95–134.CrossRefGoogle Scholar
Dritschel, D. G. 1986 The nonlinear evolution of rotating configurations of uniform vorticity. J. Fluid Mech. 172, 157–182.Google Scholar
Dritschel, D. G. 1995 A general theory for two-dimensional vortex interactions. J. Fluid Mech. 293, 269–303.CrossRefGoogle Scholar
Dritschel, D. G. & Ambaum, M. H. P. 1997 A contour-advective semi-Lagrangian algorithm for the simulation of fine-scale conservative dynamical fields. Q. J. R. Meteorol. Soc. 123, 1097–1130.Google Scholar
Dritschel, D. G., Polvani, L. M. & Mohebalhojeh, A. R. 1999 The contour-advective semi-Lagrangian algorithm for the shallow water equations. Mon. Weath. Rev. 127, 1551–1565.Google Scholar
Dritschel, D. G. & Viúdez, Á 2003 A balanced approach to modelling rotating stably stratified geophysical flows. J. Fluid Mech. 488, 123–150.CrossRefGoogle Scholar
Ford, R. 1994 The response of a rotating ellipse of uniform potential vorticity to gravity wave radiation. Phys. Fluids 6 (11), 3694–3704.CrossRefGoogle Scholar
Ford, R., McIntyre, M. E. & Norton, W. A. 2000 Balance and the slow quasimanifold: some explicit results. J. Atmos. Sci. 57, 1236–1254.Google Scholar
Garate-Lopez, I., Hueso, R., Sánchez-Lavega, A., Peralta, J., Piccioni, G. & Drossart, P. 2013 A chaotic long-lived vortex at the southern pole of Venus. Nature Geosci. 6, 254–257.Google Scholar
Griffiths, R. W. & Hopfinger, E. J. 1986 Experiments with baroclinic vortex pairs in a rotating fluid. J. Fluid Mech. 173, 501–518.Google Scholar
Griffiths, R. W. & Hopfinger, E. J. 1987 Coalescing of geostrophic vortices. J. Fluid Mech. 178, 73–97.Google Scholar
Hoskins, B. J., McIntyre, M. E. & Robertson, A. W. 1985 On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 111, 877–946.Google Scholar
Kirchhoff, G. R. 1876 Vorlesungen über mathematische Physik. Mechanik. B. G. Teubner.Google Scholar
Kizner, Z., Berson, D. & Khvoles, R. 2002 Baroclinic modon equilibria on the beta-plane: stability and transitions. J. Fluid Mech. 468, 239–270.Google Scholar
Kizner, Z., Reznik, G., Fridman, B., Khvoles, R. & McWilliams, J. C. 2008 Shallow-water modons on the $f$ -plane. J. Fluid Mech. 603, 305–329.Google Scholar
Luzzatto-Fegiz, P. & Williamson, C. H. K. 2010 Stability of elliptical vortices from ‘imperfect-velocity-impulse’ diagrams. Theor. Comput. Fluid Dyn. 24, 181–188.CrossRefGoogle Scholar
Luzzatto-Fegiz, P. & Williamson, C. H. K. 2011 An efficient and general numerical method to compute steady uniform vortices. J. Comput. Phys. 230, 6495–6511.Google Scholar
Makarov, V. G. & Kizner, Z. 2011 Stability and evolution of uniform-vorticity dipoles. J. Fluid Mech. 672, 307–325.CrossRefGoogle Scholar
Makarov, V. G., Sokolovskiy, M. A. & Kizner, Z. 2012 Doubly symmetric finite-core heton equilibria. J. Fluid Mech. 708, 397–417.CrossRefGoogle Scholar
Malanotte-Rizzoli, P. 1982 Planetary solitary waves in geophysical flows. Adv. Geophys. 24, 147–224.Google Scholar
McIntyre, M. E. & Norton, W. A. 2000 Potential vorticity inversion on a hemisphere. J. Atmos. Sci. 57, 1214–1235.2.0.CO;2>CrossRefGoogle Scholar
McKiver, W. J. & Dritschel, D. G. 2008 Balance in non-hydrostatic rotating stratified turbulence. J. Fluid Mech. 596, 201–219.Google Scholar
McWilliams, J. C. 1984 The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 146, 21–43.CrossRefGoogle Scholar
McWilliams, J. C. 1985 Submesoscale, coherent vortices in the ocean. Rev. Geophys. 23, 165–182.Google Scholar
Mohebalhojeh, A. R. 2002 On shallow water potential vorticity inversion by Rossby-number expansions. Q. J. R. Meteorol. Soc. 128, 679–694.Google Scholar
Mohebalhojeh, A. R. & Dritschel, D. G. 2000 On the representation of gravity waves in numerical models of the shallow-water equations. Q. J. R. Meteorol. Soc. 126, 669–688.Google Scholar
Nycander, J., Dritschel, D. G. & Sutyrin, G. G. 1993 The dynamics of long frontal waves in the shallow water equations. Phys. Fluids A 5, 1089–1091.Google Scholar
Olson, D. B. 1991 Rings in the ocean. Annu. Rev. Earth Planet. Sci. 19, 283–311.Google Scholar
Pedlosky, J. 1979 Geophysical Fluid Dynamics. Springer-Verlag.Google Scholar
Pierrehumbert, R. T. 1980 A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99, 129–144.Google Scholar
Płotka, H. & Dritschel, D. G. 2012 Quasi-geostrophic shallow-water vortex-patch equilibria and their stability. Geophys. Astrophys. Fluid Dyn. 106 (6), 574–595.Google Scholar
Płotka, H. & Dritschel, D. G. 2013 Quasi-geostrophic shallow-water doubly-connected vortex equilibria and their stability. J. Fluid Mech. 723, 40–68.Google Scholar
Polvani, L. M.1988 Geostrophic vortex dynamics. PhD thesis, MIT/WHOI WHOI-88-48.Google Scholar
Polvani, L. M., McWilliams, J. C., Spall, M. A. & Ford, R. 1994 The coherent structures of shallow-water turbulence: deformation-radius effects, cyclone/anticyclone asymmetry and gravity-wave generation. Chaos 4 (2), 177–186.Google Scholar
Polvani, L. M., Zabusky, N. J. & Flierl, G. R. 1989 Two-layer geostrophic vortex dynamics. Part 1. Upper-layer V-states and merger. J. Fluid Mech. 205, 215–242.Google Scholar
Ripa, P. 1987 On the stability of elliptical vortex solutions of the shallow-water equations. J. Fluid Mech. 183, 343–363.CrossRefGoogle Scholar
Saffman, P. G. & Szeto, R. 1980 Equilibrium shapes of a pair of equal uniform vortices. Phys. Fluids 23, 2339–2342.Google Scholar
Smith, R. K. & Dritschel, D. G. 2006 Revisiting the Rossby–Haurwitz wave test case with contour advection. J. Comput. Phys. 217, 473–484.Google Scholar
Stegner, A. & Dritschel, D. G. 2000 A numerical investigation of the stability of isolated shallow water vortices. J. Phys. Oceanogr. 30, 2562–2573.2.0.CO;2>CrossRefGoogle Scholar
Thomson, W. 1875 Vortex statics. Math. Phys. Pap. IV, 115–128.Google Scholar
Vallis, G. K. 2008 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar
Viúdez, Á & Dritschel, D. G. 2004 Optimal potential vorticity balance of geophysical flows. J. Fluid Mech. 521, 343–352.CrossRefGoogle Scholar
Waugh, D. W. 1992 The efficiency of symmetric vortex merger. Phys. Fluids A 4, 1745–1758.Google Scholar
Waugh, D. W. & Dritschel, D. G. 1991 The stability of filamentary vorticity in two-dimensional geophysical vortex-dynamics models. J. Fluid Mech. 231, 575–598.Google Scholar
Waugh, D. W. & Polvani, L. M. 2010 Stratospheric polar vortices. In The Stratosphere: Dynamics, Chemistry, and Transport (ed. Polvani, L. M., Sobel, A. H. & Waugh, D. W.), Geophys. Monogr. Ser., vol. 190, pp. 43–57. AGU.Google Scholar
Yasuda, I. 1995 Geostrophic vortex merger and streamer development in the ocean with special reference to the merger of Kuroshio warm core rings. J. Phys. Oceanogr. 25, 979–996.Google Scholar