Published online by Cambridge University Press: 09 September 2016
We present an exhaustive experimental and theoretical study of the shapes of simple and compound jets formed when one (simple) or two (compound) immiscible liquids are injected into another liquid. The viscosity of the co-flowing external liquid is chosen to vary the characteristic Reynolds number of the outer stream, 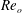 $Re_{o}$, over a wide range of values. Our slender-body theory in Gordillo et al. (J. Fluid Mech., vol. 738, 2014, pp. 335–357) is extended to predict the shapes of simple jets when
$Re_{o}$, over a wide range of values. Our slender-body theory in Gordillo et al. (J. Fluid Mech., vol. 738, 2014, pp. 335–357) is extended to predict the shapes of simple jets when 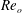 $Re_{o}$ is such that
$Re_{o}$ is such that 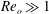 $Re_{o}\gg 1$ and also to predict the shapes of compound jets in the case of
$Re_{o}\gg 1$ and also to predict the shapes of compound jets in the case of 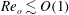 $Re_{o}\lesssim O(1)$. The validity of our theoretical results, applicable to describe the dynamics of simple or compound jets within an outer carrier fluid in a wide variety of practical situations, is tested using a set-up where the liquids flow from a pressurized chamber towards an extraction tube, finding a very good agreement between the predicted and the observed shapes. Moreover, when
$Re_{o}\lesssim O(1)$. The validity of our theoretical results, applicable to describe the dynamics of simple or compound jets within an outer carrier fluid in a wide variety of practical situations, is tested using a set-up where the liquids flow from a pressurized chamber towards an extraction tube, finding a very good agreement between the predicted and the observed shapes. Moreover, when 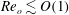 $Re_{o}\lesssim O(1)$, and thanks to the fact that the liquid jets produced using our method are highly stretched in the downstream direction, we find that the values of the critical capillary number above which a steady stretched jet is produced, with the capillary number defined here using the outer stream velocity and viscosity, is well below the corresponding critical values characterizing other similar procedures, like flow focusing. This experimental result, which is supported by a spatio-temporal stability analysis in which the axial gradients of the unperturbed solution are retained in the dispersion relation, imply a substantial saving of energy and of the volume of outer liquid necessary to generate a steady capillary jet from which drops are regularly produced. Additionally, making use of continuity arguments and of the fact that drops are formed as a consequence of the growth of a capillary instability, we provide closed expressions for the drop diameters and their production frequencies when the capillary number is above the critical one, in very good agreement with experiments. The simple or double microemulsions generated by the capillary disintegration of the type of simple or compound highly stretched steady jets described here might find applications in biotechnology, pharmacy, cosmetics or materials science.
$Re_{o}\lesssim O(1)$, and thanks to the fact that the liquid jets produced using our method are highly stretched in the downstream direction, we find that the values of the critical capillary number above which a steady stretched jet is produced, with the capillary number defined here using the outer stream velocity and viscosity, is well below the corresponding critical values characterizing other similar procedures, like flow focusing. This experimental result, which is supported by a spatio-temporal stability analysis in which the axial gradients of the unperturbed solution are retained in the dispersion relation, imply a substantial saving of energy and of the volume of outer liquid necessary to generate a steady capillary jet from which drops are regularly produced. Additionally, making use of continuity arguments and of the fact that drops are formed as a consequence of the growth of a capillary instability, we provide closed expressions for the drop diameters and their production frequencies when the capillary number is above the critical one, in very good agreement with experiments. The simple or double microemulsions generated by the capillary disintegration of the type of simple or compound highly stretched steady jets described here might find applications in biotechnology, pharmacy, cosmetics or materials science.