Article contents
Shock–shock interactions in granular flows
Published online by Cambridge University Press: 17 December 2019
Abstract
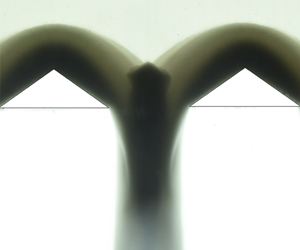
Shock–shock interaction structures and a newly discovered dynamic instability in granular streams resulting from such interactions are presented. Shock waves are generated by placing two similar triangular wedges in a gravity-driven granular stream. When the shock waves interact, grains collapse near the centre region of the wedges and a slow-moving concentrated diamond-shaped streak of grains is formed that grows as the inclination of the channel is increased. The diamond streak, under certain geometric conditions, is found to become unstable and start oscillating in the direction transverse to the mainstream. When the wedges are placed too close to each other, the granular flux of the incoming stream is unable to pass through the small gap, resulting in the formation of a single bow shock enveloping both the wedges. Experiments are performed for a wide range of flow speeds, wedge angles and wedge separations to investigate the interaction zone. We discuss a possible mechanism for the formation of the central streak and the associated dynamic instability observed for specific physical parameters.
JFM classification
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
Khan et al. supplementary movie 1
Shock-shock interactions for Wedge angle = 60 degrees, Wedge spacing = 1d and channel inclination = 55 degrees at frame rate = 60 fps.
Khan et al. supplementary movie 2
Shock-shock interactions for Wedge angle = 60 degrees, Wedge spacing = 1d and channel inclination = 60 degrees at frame rate = 60 fps.
- 15
- Cited by


