Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T02:33:21.237Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock formation in two-layer equal-density viscous gravity currents

Published online by Cambridge University Press:  25 January 2019

Tim-Frederik Dauck Open the ORCID record for Tim-Frederik Dauck [Opens in a new window] ,
Finn Box Open the ORCID record for Finn Box [Opens in a new window] ,
Laura Gell ,
Jerome A. Neufeld Open the ORCID record for Jerome A. Neufeld [Opens in a new window]  and
John R. Lister Open the ORCID record for John R. Lister [Opens in a new window]
Tim-Frederik Dauck*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
Finn Box
Affiliation:
BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK Bullard Laboratories, Department of Earth Sciences, University of Cambridge, Cambridge CB3 0WA, UK
Laura Gell
Affiliation:
BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK
Jerome A. Neufeld
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK Bullard Laboratories, Department of Earth Sciences, University of Cambridge, Cambridge CB3 0WA, UK
John R. Lister
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The flow of a viscous gravity current over a lubricating layer of fluid is modelled using lubrication theory. We study the case of an axisymmetric current with constant influx which allows for a similarity solution, which depends on three parameters: a non-dimensional influx rate ${\mathcal{Q}}$; a viscosity ratio 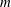$m$ between the lower and upper layer fluid; and a relative density difference $\unicode[STIX]{x1D700}$. The limit of equal densities 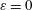$\unicode[STIX]{x1D700}=0$ is singular, as the interfacial evolution equation changes nature from parabolic to hyperbolic. Theoretical analysis of this limit reveals that a discontinuity, or shock, in the interfacial height forms above a critical viscosity ratio $m_{crit}=3/2$, i.e. for a sufficiently less viscous upper-layer fluid. The physical mechanism for shock formation is described, which is based on advective steepening of the interface between the two fluids and relies on the lack of a contribution to the pressure gradient from the interfacial slope for equal-density fluids. In the limit of small but non-zero density differences, local travelling-wave solutions are found which regularise the singular structure of a potential shock and lead to a constraint on the possible shock heights in the form of an Oleinik entropy condition. Calculation of a simplified time-dependent system reveals the appropriate boundary conditions for the late-time similarity solution, which includes a shock at the nose of the current for 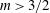$m>3/2$. The numerically calculated similarity solutions compare well to experimental measurements with respect to the predictions of self-similarity, the radial extent and the self-similar top-surface shapes of the current.

JFM classification

Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 730 - 756
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acton, J. M., Huppert, H. E. & Worster, M. G. 2001 Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 440, 359–380.10.1017/S0022112001004700Google Scholar
Balmforth, N. J., Craster, R. V., Perona, P., Rust, A. C. & Sassi, R. 2007 Viscoplastic dam breaks and the Bostwick consistometer. J. Non-Newtonian Fluid Mech. 142, 63–78.10.1016/j.jnnfm.2006.06.005Google Scholar
Billingham, J. & King, A. C. 2001 Wave Motion. Cambridge University Press.10.1017/CBO9780511841033Google Scholar
Bischofberger, I., Ramachandran, R. & Nagel, S. R. 2014 Fingering versus stability in the limit of zero interfacial tension. Nat. Commun. 5, 5265.10.1038/ncomms6265Google Scholar
Chen, C.-Y. & Meiburg, E. 1996 Miscible displacements in capillary tubes. Part 2. Numerical simulations. J. Fluid Mech. 326, 57–90.10.1017/S0022112096008245Google Scholar
D’Errico, G., Ortona, O., Capuano, F. & Vitagliano, V. 2004 Diffusion coefficients for the binary system glycerol + water at 25 °C. A velocity correlation study. J. Chem. Engng Data 49, 1665–1670.10.1021/je049917uGoogle Scholar
Diez, J. A., Gratton, R. & Gratton, J. 1992 Self-similar solution of the second kind for a convergent viscous gravity current. Phys. Fluids 4, 1148–1155.10.1063/1.858233Google Scholar
Doedel, E. J., Fairgrieve, T. F., Sanstede, B., Champneys, A. R., Kuznetsov, Y. A. & Wang, X.2007 AUTO-07P: Continuation and bifurcation software for ordinary differential equations. http://indy.cs.concordia.ca/auto/.Google Scholar
Fink, J. H. & Griffiths, R. W. 1998 Morphology, eruption rates, and rheology of lava domes: Insights from laboritory models. J. Geophys. Res. 103, 527–545.10.1029/97JB02838Google Scholar
Gratton, J. & Minotti, F. 1990 Self-similar viscous gravity currents: phase-plane formalism. J. Fluid Mech. 210, 155–182.10.1017/S0022112090001240Google Scholar
Gratton, J. & Minotti, F. 1999 Theory of creeping gravity currents of a non-Newtonian liquid. Phys. Rev. E 60, 6960–6967.Google Scholar
Griffiths, R. W. 2000 The dynamics of lava flows. Annu. Rev. Fluid Mech. 32, 477–518.10.1146/annurev.fluid.32.1.477Google Scholar
Griffiths, R. W. & Fink, J. 1993 Effects of surface cooling on the spreading of lava flows and domes. J. Fluid Mech. 252, 667–702.10.1017/S0022112093003933Google Scholar
Hewitt, I. J., Balmforth, N. J. & De Bruyn, J. R. 2015 Elastic-plated gravity currents. Eur. J. Appl. Maths 26, 1–31.10.1017/S0956792514000291Google Scholar
Hogg, A. J. & Matson, G. P. 2009 Slumps of viscoplastic fluids on slopes. J. Non-Newtonian Fluid Mech. 158, 101–112.10.1016/j.jnnfm.2008.07.003Google Scholar
Hoult, D. P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4, 341–368.10.1146/annurev.fl.04.010172.002013Google Scholar
Huppert, H. E. 1982a Flow and instability of a viscous current down a slope. Nature 300, 427–429.10.1038/300427a0Google Scholar
Huppert, H. E. 1982b Propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.10.1017/S0022112082001797Google Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.10.1017/S002211200600930XGoogle Scholar
Jacobs, D., McKinney, B. & Shearer, M. 1995 Traveling wave solutions of the modified Korteweg–deVries–Burgers equation. J. Differ. Equ. 116, 448–467.10.1006/jdeq.1995.1043Google Scholar
Kerr, R. C. & Lister, J. R. 1987 The spread of subducted lithospheric material along the mid-mantle boundary. Earth Planet. Sci. Lett. 85, 241–247.10.1016/0012-821X(87)90034-3Google Scholar
Koch, D. M. & Koch, D. L. 1995 Numerical and theoretical solutions for a drop spreading below a free fluid surface. J. Fluid Mech. 287, 251–278.10.1017/S0022112095000942Google Scholar
Kowal, K. N. & Worster, M. G. 2015 Lubricated viscous gravity currents. J. Fluid Mech. 766, 626–655.10.1017/jfm.2015.30Google Scholar
Lajeunesse, E., Martin, J., Rakotomalala, N. & Salin, D. 1997 3D instability of miscible displacements in a Hele-Shaw cell. Phys. Rev. Lett. 79, 5254–5257.10.1103/PhysRevLett.79.5254Google Scholar
Lajeunesse, E., Martin, J., Rakotomalala, N., Salin, D. & Yortsos, Y. C. 1999 Miscible displacement in a Hele-Shaw cell at high rates. J. Fluid Mech. 398, 299–319.10.1017/S0022112099006357Google Scholar
Lajeunesse, E., Martin, J., Rakotomalala, N., Salin, D. & Yortsos, Y. C. 2001 The threshold of the instability in miscible displacements in a Hele-Shaw cell at high rates. Phys. Fluids 13, 799–801.10.1063/1.1347959Google Scholar
LeFloch, P. G. 2002 Hyperbolic Systems of Conservation Laws: The Theory of Classical and Nonclassical Shock Waves. Birkhäuser.10.1007/978-3-0348-8150-0Google Scholar
Lister, J. R. 1992 Viscous flows down an inclined plane from point and line sources. J. Fluid Mech. 242, 631–653.10.1017/S0022112092002520Google Scholar
Lister, J. R. & Kerr, R. C. 1989 The propagation of two-dimensional and axisymmetric viscous gravity currents at a fluid interface. J. Fluid Mech. 203, 215–249.10.1017/S0022112089001448Google Scholar
Lister, J. R., Peng, G. G. & Neufeld, J. A. 2013 Viscous control of peeling an elastic sheet by bending and pulling. Phys. Rev. Lett. 111, 154501.10.1103/PhysRevLett.111.154501Google Scholar
Mathunjwa, J. S. & Hogg, A. J. 2006 Self-similar gravity currents in porous media: Linear stability of the Barenblatt–Pattle solution revisited. Eur. J. Mech. (B/Fluids) 25, 360–378.10.1016/j.euromechflu.2005.09.005Google Scholar
Neufeld, J. A., Vella, D., Huppert, H. E. & Lister, J. R. 2011 Leakage from gravity currents in a porous medium. Part 1. A localized sink. J. Fluid Mech. 666, 391–413.10.1017/S002211201000488XGoogle Scholar
Nye, J. F. 1952 The mechanics of glacier flow. J. Glaciol. 2, 82–93.10.1017/S0022143000033967Google Scholar
Paterson, L. 1985 Fingering with miscible fluids in a Hele Shaw cell. Phys. Fluids 28, 26–30.10.1063/1.865195Google Scholar
Petitjeans, P. & Maxworthy, T. 1996 Miscible displacements in capillary tubes. Part 1. Experiments. J. Fluid Mech. 326, 37–56.10.1017/S0022112096008233Google Scholar
Pritchard, D. & Hogg, A. J. 2002 Draining viscou gravity currents in a vertical fracture. J. Fluid Mech. 459, 207–216.10.1017/S0022112002008327Google Scholar
Rakotomalala, N., Salin, D. & Watzky, P. 1996 Simulations of viscous flows of complex fluids with a Bhatnagar, Gross, and Krook lattice gas. Phys. Fluids 8, 3200–3202.10.1063/1.869093Google Scholar
Saffman, P. G. 1986 Viscous fingering in Hele-Shaw cells. J. Fluid Mech. 173, 73–94.10.1017/S0022112086001088Google Scholar
Saffman, P. G. & Taylor, G. I. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A 245, 312–329.Google Scholar
Sayag, R. & Worster, M. G. 2013 Axisymmetric gravity currents of power-law fluids over a rigid horizontal surface. J. Fluid Mech. 716, R5.10.1017/jfm.2012.545Google Scholar
Schoof, C. & Hewitt, I. 2013 Ice-sheet dynamics. Annu. Rev. Fluid Mech. 45, 217–239.10.1146/annurev-fluid-011212-140632Google Scholar
Smith, P. C. 1973 A similarity solution for slow viscous flow down an inclined plane. J. Fluid Mech. 58, 275–288.10.1017/S0022112073002594Google Scholar
Smith, S. H. 1969 On initial value problems for the flow in a thin sheet of viscous liquid. Z. Angew. Math. Phys. 20, 556–560.10.1007/BF01595050Google Scholar
Wooding, R. A. 1969 Growth of fingers at an unstable diffusive interface in a porous medium or Hele-Shaw cell. J. Fluid Mech. 39, 477–495.10.1017/S002211206900228XGoogle Scholar
Yang, Z. & Yortsos, Y. C. 1997 Asymptotic solutions of miscible displacements in geometries of large aspect ratio. Phys. Fluids 9, 286–298.10.1063/1.869149Google Scholar
Zheng, Z., Christov, I. C. & Stone, H. A. 2014 Influence of heterogeneity on second-kind self-similar solutions for viscous gravity currents. J. Fluid Mech. 747, 218–246.10.1017/jfm.2014.148Google Scholar