Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T12:14:16.142Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock dispersal of dilute particle clouds

Published online by Cambridge University Press:  27 February 2018

Theo G. Theofanous Open the ORCID record for Theo G. Theofanous [Opens in a new window] ,
Vladimir Mitkin  and
Chih-Hao Chang
Theo G. Theofanous*
Affiliation:
Chemical Engineering Department, University of California, Santa Barbara, CA 93106, USA
Vladimir Mitkin
Affiliation:
Aerospace Research Laboratory, University of Virginia, VA 22904, USA
Chih-Hao Chang
Affiliation:
Theofanous Co. Inc., Santa Barbara, CA 93109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

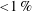We present experiments and numerical simulations for an elementary paradigm of disperse multiphase flow: highly dilute, homogeneous, finite-dimension clouds of particles (curtains) hit by shock/blast waves in one dimension. In the experiments (particle volume fraction ${<}1\,\%$) the blasts that follow the shocks vary from low subsonic to supersonic, and we report data on curtain expansions and volume fraction distributions. The particle-resolving numerical simulations, run for the supersonic case, yield excellent agreement with all of these experimental data. We find that the essential feature for these good predictions is a flow choking phenomenon that entails a (particle) dispersive character of the flow down a volume fraction gradient (as at the downstream portions of the curtain). A most basic effective-field model is made to capture this gas dynamics by emulating the wake behind each particle, as seen in the particle-resolving direct Euler simulation (DES). On this basis, standard drag laws yield excellent agreement with the dispersive behaviour found in the experiment/DES, thus revealing a physics-based path to eventual well posedness of the mathematical model.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Particle/fluid flow Compressible Flows: Shock waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 841 , 25 April 2018 , pp. 732 - 745
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, A. B. & Hiatt, J.1971 Free-flight measurements of sphere drag at subsonic, transonic, supersonic, and hypersonic speeds for continuum, transition, and near-free-molecular flow conditions. AEDC-TR-70-291.Google Scholar
Houim, R. W. & Oran, E. S. 2016 A multiphase model for compressible granular gaseous flows: formulation and initial tests. J. Fluid Mech. 789, 166–220.Google Scholar
Lhuillier, D., Chang, C.-H. & Theofanous, T. G. 2013 On the quest for a hyperbolic effective-field model of disperse flows. J. Fluid Mech. 731, 184–194.Google Scholar
Ling, Y., Wagner, J. L., Beresh, S. J., Kearney, S. P. & Balachandar, S. 2012 Interaction of a planar shock wave with a dense particle curtain: modeling and experiments. Phys. Fluids 24, 113301.Google Scholar
Saurel, R., Chinnayya, A. & Carmouze, Q. 2017 Modelling compressible dense and dilute two-phase flows. Phys. Fluids 29, 063301.Google Scholar
Theofanous, T. G. & Chang, C.-H. 2016 The dynamics of dense particle clouds subjected to shock waves. Part II. Modelling/numerical issues and the way forward. Intl J. Multiphase Flow 89, 177–206.Google Scholar
Theofanous, T. G., Mitkin, V. & Chang, C.-H. 2016 The dynamics of dense particle clouds subjected to shock waves. Part I. Experiments and scaling laws. J. Fluid Mech. 792, 655–681.Google Scholar
Wagner, J. L., Beresh, S. J., Kearney, S. P., Trott, W. M., Castaneda, J. N., Pruett, B. O. & Baer, M. R. 2012 A multiphase shock tube for shock wave interactions with dense particle fields. Exp. Fluids 52, 1507–1517.Google Scholar
Zhang, Z. D. & Prosperetti, A. 1994 Average equations for inviscid disperse two-phase flow. J. Fluid Mech. 276, 185–219.Google Scholar
Supplementary material: File

Theofanous et al. supplementary material

Theofanous et al. supplementary material 1

Download Theofanous et al. supplementary material(File)
File 14 MB