Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T09:37:26.305Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear generation in a confined, composite layer of cross-bedded porous rock

Published online by Cambridge University Press:  29 July 2020

Neeraja Bhamidipati Open the ORCID record for Neeraja Bhamidipati [Opens in a new window]  and
Andrew W. Woods Open the ORCID record for Andrew W. Woods [Opens in a new window]
Neeraja Bhamidipati*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, CambridgeCB3 0EZ, UK
Andrew W. Woods
Affiliation:
BP Institute, University of Cambridge, Madingley Road, CambridgeCB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

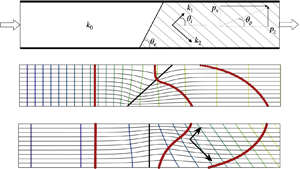
We study the longitudinal spreading of a passive tracer by a two-dimensional pressure-driven flow through a composite layer of porous rock which is bounded above and below by impermeable seal rock. We focus on the flow across the interface between two neighbouring zones of the rock. First, we show that, with isotropic permeability, if the interface between the two zones is tilted relative to the boundaries, then this results in a difference in travel times across the formation which in turns leads to a net shear flow. We explore the strength of this shear as a function of (a) the permeability ratio across the interface, and (b) the interface angle. Second, we show that if one zone of the rock is cross-bedded, then with uniform flow, the pressure gradient is directed at an angle to the boundary. As a result, there is a transition zone across the interface, which again leads to a net shear, even if the interface is normal to the boundaries of the layer. We explore the competition between these effects, showing how they may combine constructively to produce a larger shear, or may negate one another, reducing or reversing the sign of the shear, depending on the angle of the interface, the degree of anisotropy and the change in effective downstream permeability across the interface. We discuss some of the implications of this shear for modelling flow in such composite rocks.

JFM classification

Low-Reynolds-number flows: Porous media
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 899 , 25 September 2020 , R3
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Allen, J. R. L. 1963 The classification of cross-stratified units. With notes on their origin. Sedimentology 2 (2), 93–114.CrossRefGoogle Scholar
Bear, J. 1971 Dynamics of Flow in Porous Media. Elsevier.Google Scholar
Begg, S. H. & King, P. R. 1985 Modelling the effects of shales on reservoir performance: calculation of effective vertical permeability. In SPE Reservoir Simulation Symposium. Society of Petroleum Engineers.CrossRefGoogle Scholar
Burns, K. J., Vasil, G. M., Oishi, J. S., Lecoanet, D. & Brown, B. P. 2019 Dedalus: a flexible framework for numerical simulations with spectral methods. arXiv:1905.10388.CrossRefGoogle Scholar
Castle, J. W., Molz, F. J., Lu, S. & Dinwiddie, C. L. 2004 Sedimentology and fractal-based analysis of permeability data, John Henry Member, Straight Cliffs Formation (Upper Cretaceous), Utah, USA. J. Sedim. Res. 74 (2), 270–284.CrossRefGoogle Scholar
Corbett, P. & Jensen, J. L. 1992 Estimating the mean permeability: how many measurements do you need? First Break 10 (3), 89–94.CrossRefGoogle Scholar
Dagan, G. 1979 Models of groundwater flow in statistically homogeneous porous formations. Water Resour. Res. 15 (1), 47–63.CrossRefGoogle Scholar
Davis, J. M., Lohmann, R. C., Phillips, F. M., Wilson, J. L. & Love, D. W. 1993 Architecture of the Sierra Ladrones formation, central New Mexico: depositional controls on the permeability correlation structure. Geol. Soc. Am. Bull. 105 (8), 998–1007.2.3.CO;2>CrossRefGoogle Scholar
Dawe, R. A., Caruana, A. & Grattoni, C. A. 2011 Immiscible displacement in cross-bedded heterogeneous porous media. Transp. Porous Media 87 (1), 335–353.CrossRefGoogle Scholar
Desbarats, A. 1989 Support effects and the spatial averaging of transport properties. Math. Geol. 21 (3), 383–389.CrossRefGoogle Scholar
Deutsch, C. 1989 Calculating effective absolute permeability in sandstone/shale sequences. SPE Formation Eval. 4 (03), 343–348.CrossRefGoogle Scholar
Durlofsky, L. J. 1991 Numerical calculation of equivalent grid block permeability tensors for heterogeneous porous media. Water Resour. Res. 27 (5), 699–708.CrossRefGoogle Scholar
Goggin, D. J., Chandler, M. A., Kocurek, G. T. & Lake, L. W. 1988 Patterns of permeability in eolian deposits: page sandstone (Jurassic), northeastern Arizona. SPE Formation Eval. 3 (02), 297–306.CrossRefGoogle Scholar
Hartkamp, C. A., Arribas, J. & Tortosa, A. 1993 Grain size, composition, porosity and permeability contrasts within cross-bedded sandstones in tertiary fluvial deposits, Central Spain. Sedimentology 40 (4), 787–799.CrossRefGoogle Scholar
Huysmans, M., Peeters, L., Moermans, G. & Dassargues, A. 2008 Relating small-scale sedimentary structures and permeability in a cross-bedded aquifer. J. Hydrol. 361 (1–2), 41–51.CrossRefGoogle Scholar
Klise, K. A., Tidwell, V. C. & McKenna, S. A. 2008 Comparison of laboratory-scale solute transport visualization experiments with numerical simulation using cross-bedded sandstone. Adv. Water Resour. 31 (12), 1731–1741.CrossRefGoogle Scholar
Nordahl, K. & Ringrose, P. S. 2008 Identifying the representative elementary volume for permeability in heterolithic deposits using numerical rock models. Math. Geosci. 40 (7), 753–771.CrossRefGoogle Scholar
Pickup, G. E., Ringrose, P. S., Corbett, P. W. M., Jensen, J. L. & Sorbie, K. S. 1995 Geology, geometry and effective flow. Petrol. Geosci. 1 (1), 37–42.CrossRefGoogle Scholar
Sawyer, A. H. & Cardenas, M. B. 2009 Hyporheic flow and residence time distributions in heterogeneous cross-bedded sediment. Water Resour. Res. 45, W08406.CrossRefGoogle Scholar
Tidwell, V. C. & Wilson, J. L. 2000 Heterogeneity, permeability patterns, and permeability upscaling: physical characterization of a block of Massillon sandstone exhibiting nested scales of heterogeneity. Tech. Rep. SAND2000-0999J. Sandia National Labs, Albuquerque, NM, US.CrossRefGoogle Scholar
Woods, A. W. 2015 Flow in Porous Rocks. Cambridge University Press.CrossRefGoogle Scholar