Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T01:35:08.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-similar kinematics among efficient slender swimmers

Published online by Cambridge University Press:  07 February 2018

A. J. Wiens Open the ORCID record for A. J. Wiens [Opens in a new window]  and
A. E. Hosoi
A. J. Wiens*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02143, USA
A. E. Hosoi
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02143, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an analysis of efficient undulatory propulsion for slender animals swimming at high Reynolds number. Using Lighthill’s large-amplitude elongated-body theory, we show that optimally efficient swimming kinematics can be characterized through a single dimensionless variable 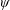$\unicode[STIX]{x1D713}$. This variable, 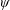$\unicode[STIX]{x1D713}$, is defined by a simple function of a swimming animal’s body wave properties. Physically, $\unicode[STIX]{x1D713}$ characterizes how the velocity of an animal’s tail varies throughout its swimming stroke. Lighthill’s model predicts that swimming efficiency is near optimal in the range 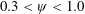$0.3<\unicode[STIX]{x1D713}<1.0$ and peaks at $\unicode[STIX]{x1D713}=0.87$. At this point, the average magnitude of the tail velocity is minimized and swimming kinematics are tuned such that the thrust coefficient is as close to constant as possible throughout the swimming stroke. We use a compiled dataset of over 250 unique measurements to show that species across a wide range of size and shape fall within the optimal region.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Propulsion Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 106 - 130
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bainbridge, R. 1958 The speed of swimming of fish as related to size and to the frequency and amplitude of the tail beat. J. Expl Biol. 35 (1), 109–133.CrossRefGoogle Scholar
Bandyopadhyay, P. R., Beal, D. N., Hrubes, J. D. & Mangalam, A. 2012 Relationship of roll and pitch oscillations in a fin flapping at transitional to high Reynolds numbers. J. Fluid Mech. 702, 298–331.Google Scholar
Blake, R., Li, J. & Chan, K. 2009 Swimming in four goldfish Carassius auratus morphotypes: understanding functional design and performance employing artificially selected forms. J. Fish Biol. 75 (3), 591–617.Google Scholar
Clark, R. P. & Smits, A. J. 2006 Thrust production and wake structure of a batoid-inspired oscillating fin. J. Fluid Mech. 562, 415–429.Google Scholar
Dabiri, J. O. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41 (1), 17–33.Google Scholar
Eloy, C. 2012 Optimal Strouhal number for swimming animals. J. Fluids Struct. 30, 205–218.Google Scholar
Eloy, C. 2013 On the best design for undulatory swimming. J. Fluid Mech. 717, 48–89.Google Scholar
Gazzola, M., Argentina, M. & Mahadevan, L. 2014 Scaling macroscopic aquatic locomotion. Nat. Phys. 10 (10), 758–761.Google Scholar
Gray, J. 1936 Studies in animal locomotion: VI. The propulsive powers of the dolphin. J. Expl Biol. 13 (2), 192–199.Google Scholar
Hover, F. S., Haugsdal, O. & Triantafyllou, M. S. 2004 Effect of angle of attack profiles in flapping foil propulsion. J. Fluids Struct. 19 (1), 37–47.Google Scholar
Jayne, B. C. & Lauder, G. V. 1995 Speed effects on midline kinematics during steady undulatory swimming of largemouth bass, Micropterus salmoides . J. Expl Biol. 198 (2), 585–602.Google Scholar
Keller, J. B. 1974 Optimal velocity in a race. Am. Math. Mon. 81 (5), 474–480.Google Scholar
Kern, S. & Koumoutsakos, P. 2006 Simulations of optimized anguilliform swimming. J. Expl Biol. 209 (24), 4841–4857.CrossRefGoogle ScholarPubMed
Langerhans, R. B. 2009 Trade-off between steady and unsteady swimming underlies predator-driven divergence in Gambusia affinis . J. Evol. Biol. 22 (5), 1057–1075.Google Scholar
van Leeuwen, J. L., Voesenek, J. & Müller, U. K. 2015 How body torque and Strouhal number change with swimming speed and developmental stage in larval zebrafish. J. R. Soc. Interface 12 (110), 20150479.Google Scholar
Liao, J. C. 2002 Swimming in needlefish (Belonidae): anguilliform locomotion with fins. J. Expl Biol. 205 (18), 2875–2884.Google Scholar
Lighthill, M. J. 1960 Note on the swimming of slender fish. J. Fluid Mech. 9 (2), 305–317.Google Scholar
Lighthill, M. J. 1969 Hydromechanics of aquatic animal propulsion. Annu. Rev. Fluid Mech. 1, 413–446.Google Scholar
Lighthill, M. J. 1971 Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 179 (1055), 125–138.Google Scholar
Lighthill, S. 1975 Mathematical Biofluiddynamics. Society for Industrial and Applied Mathematics.Google Scholar
Linden, P. F. & Turner, J. S. 2001 The formation of optimal vortex rings, and the efficiency of propulsion devices. J. Fluid Mech. 427, 61–72.Google Scholar
Linden, P. F. & Turner, J. S. 2004 Optimal vortex rings and aquatic propulsion mechanisms. Proc. R. Soc. 271 (1539), 647–653.Google Scholar
Long, J., Hale, M., McHenry, M. & Westneat, M. 1996 Functions of fish skin: flexural stiffness and steady swimming of longnose gar, Lepisosteus osseus . J. Expl Biol. 199 (10), 2139–2151.Google Scholar
Maertens, A. P., Gao, A. & Triantafyllou, M. 2017 Optimal undulatory swimming for a single fish-like body and for a pair of interacting swimmers. J. Fluid Mech. 813, 301–345.Google Scholar
von Mises, L. 1959 Theory of Flight. Dover Publications.Google Scholar
Moored, K. W., Dewey, P. A., Boschitsch, B. M., Smits, A. J. & Haj-Hariri, H. 2014 Linear instability mechanisms leading to optimally efficient locomotion with flexible propulsors. Phys. Fluids 26 (4), 041905.Google Scholar
Moored, K. W., Dewey, P. A., Smits, A. J. & Haj-Hariri, H. 2012 Hydrodynamic wake resonance as an underlying principle of efficient unsteady propulsion. J. Fluid Mech. 708, 329–348.Google Scholar
Muller, U. K., Smit, J., Stamhuis, E. J. & Videler, J. J. 2001 How the body contributes to the wake in undulatory fish swimming. J. Expl Biol. 204 (16), 2751–2762.Google Scholar
Prempraneerach, P., Hover, F. S. & Triantafyllou, M. S. 2003 The effect of chordwise flexibility on the thrust and efficiency of a flapping foil. In UUST 03: 13th International Symposium on Unmanned Untethered Submersible Technology, pp. 1–10.Google Scholar
Raspa, V., Ramananarivo, S., Thiria, B. & Godoy-Diana, R. 2014 Vortex-induced drag and the role of aspect ratio in undulatory swimmers. Phys. Fluids 26 (4), 041701.Google Scholar
van Rees, W., Gazzola, M. & Koumoutsakos, P. 2013 Optimal shapes for anguilliform swimmers at intermediate Reynolds numbers. J. Fluid Mech. 722, R3.CrossRefGoogle Scholar
van Rees, W., Gazzola, M. & Koumoutsakos, P. 2015 Optimal morphokinematics for undulatory swimmers at intermediate Reynolds numbers. J. Fluid Mech. 775, 178–188.Google Scholar
Rohr, J. J. 2004 Strouhal numbers and optimization of swimming by odontocete cetaceans. J. Expl Biol. 207 (10), 1633–1642.Google Scholar
Taylor, G. 1952 Analysis of the swimming of long and narrow animals. Proc. R. Soc Lond. A 214 (1117), 158–183.Google Scholar
Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. 2003 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 425 (6959), 707–711.Google Scholar
Tokić, G. & Yue, D. K. P. 2012 Optimal shape and motion of undulatory swimming organisms. Proc. Biol. Sci. 279 (1740), 3065–3074.Google Scholar
Triantafyllou, G. S., Triantafyllou, M. S. & Grosenbaugh, M. 1993 Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 7 (2), 205–224.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Gopalkrishnan, R. 1991 Wake mechanics for thrust generation in oscillating foils. Phys. Fluids 3 (12), 2835.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Yue, D. K. P. 2000 Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32 (1), 33–53.Google Scholar
Tytell, E. D., Borazjani, I., Sotiropoulos, F., Baker, T. V., Anderson, E. J. & Lauder, G. V. 2010 Disentangling the functional roles of morphology and motion in the swimming of fish. Integr. Compar. Biol. 50 (6), 1140–1154.Google Scholar
Videler, J. J. 1993 Fish Swimming. Chapman & Hall.Google Scholar
Videler, J. J. & Hess, F. 1984 Fast continuous swimming of two pelagic predators, saithe (Pollachius virens) and mackerel (Scomber scombrus): a kinematic analysis. J. Expl Biol. 109 (1), 209–228.Google Scholar
Videler, J. J. & Wardle, C. S. 1978 New kinematic data from high-speed cine film recordings of swimming cod (Gadus morhua). Netherlands J. Zool. 28 (3-4), 465–484.Google Scholar
Webb, P. W. 1986 Kinematics of lake sturgeon, Acipenser fulvescens, at cruising speeds. Can. J. Zool. 64 (10), 2137–2141.Google Scholar
Webb, P. W. & Keyes, R. S. 1982 Swimming kinematics of sharks. Fishery Bull. 80 (4), 803–812.Google Scholar
Webb, P. W., Kostecki, P. T. & Stevens, E. D. 1984 The effect of size and swimming speed on locomotor kinematics of rainbow trout. J. Expl Biol. 109 (1), 77–95.Google Scholar
van Weerden, J. F., Reid, D. P. & Hemelrijk, C. K. 2014 A meta-analysis of steady undulatory swimming. Fish Fisheries 15 (3), 397–409.Google Scholar
Wu, T. Y. 1971 Hydromechanics of swimming propulsion. Part 3. Swimming and optimum movements of slender fish with side fins. J. Fluid Mech. 46 (3), 545–568.Google Scholar
Supplementary material: File

Wiens and Hosoi supplementary material

Wiens and Hosoi supplementary material 1

Download Wiens and Hosoi supplementary material(File)
File 263 KB