Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-24T16:18:30.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-selection of flow instabilities by acoustic perturbations around rectangular cylinder in cross-flow

Published online by Cambridge University Press:  04 November 2024

Atef Mohany Open the ORCID record for Atef Mohany [Opens in a new window] ,
Ahmed Shoukry Open the ORCID record for Ahmed Shoukry [Opens in a new window]  and
Luc Pastur Open the ORCID record for Luc Pastur [Opens in a new window]
Atef Mohany
Affiliation:
Ontario Tech University, Oshawa, ON L1H 4X8, Canada
Ahmed Shoukry
Affiliation:
Ontario Tech University, Oshawa, ON L1H 4X8, Canada
Luc Pastur*
Affiliation:
Fluid Mechanics Department, ENSTA Paris, Institut Polytechnique de Paris, F-91120 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

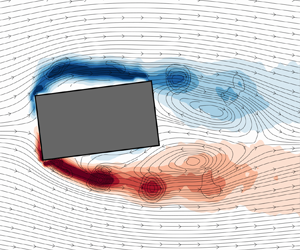
This work experimentally investigates the flow structure around a rectangular cylinder with an aspect ratio of 2 under varying incidence angles to examine how acoustic perturbations modify and modulate the unsteady flow instabilities. In the absence of acoustic excitation, the angle of incidence is found to markedly influence the flow topology and the natural shedding pattern altering the vortex formation length and wake dynamics. With acoustic perturbations, it is observed that for incidence angles $\alpha = 0^{\circ }$ and $\alpha = 5^{\circ }$, the masked impinging leading-edge vortex (ILEV)/trailing-edge vortex shedding (TEVS) instability modes of $n= 1$ and $n= 2$ become evident when their frequencies coincide with the frequencies of the acoustic perturbations (i.e. resonant condition). Both trailing-edge and leading-edge vortices were found to be modulated by the acoustic pressure cycle. These instability modes, which are naturally present under non-resonant conditions for significantly higher aspect ratios, highlight the role of incidence angle and self-excited acoustic resonance in virtually augmenting the streamwise length of the cylinder, thereby facilitating the emergence and sustenance of the ILEV/TEVS shedding pattern.

JFM classification

Acoustics: Aeroacoustics Wakes/Jets: Wakes Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 998 , 10 November 2024 , A51
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alziadeh, M. & Mohany, A. 2023 Flow structure and aerodynamic forces of finned cylinders during flow-induced acoustic resonance. J. Fluids Struct. 119, 103887.CrossRefGoogle Scholar
Blevins, R.D. 1984 Review of sound induced by vortex shedding from cylinders. J. Sound Vib. 92 (4), 455–470.CrossRefGoogle Scholar
Cheng, M., Whyte, D.S. & Lou, J. 2007 Numerical simulation of flow around a square cylinder in uniform-shear flow. J. Fluids Struct. 23 (2), 207–226.CrossRefGoogle Scholar
Durão, D.F.G., Heitor, M.V. & Pereira, J.C.F. 1988 Measurements of turbulent and periodic flows around a square cross-section cylinder. Exp. Fluids 6, 298–304.CrossRefGoogle Scholar
Dutta, S., Muralidhar, K. & Panigrahi, P. 2003 Influence of the orientation of a square cylinder on the wake properties. Exp. Fluids 34, 16–23.CrossRefGoogle Scholar
Hourigan, K., Thompson, M.C. & Tan, B.T. 2001 Self-sustained oscillations in flows around long blunt plates. J. Fluids Struct. 15, 387–398.CrossRefGoogle Scholar
Howe, M.S. 1980 The dissipation of sound at an edge. J. Sound Vib. 70, 407–411.CrossRefGoogle Scholar
Howe, M.S. 1997 Sound generated by fluid-structure interactions. Comput. Struct. 65, 433–446.CrossRefGoogle Scholar
Hu, J., Zhou, Y. & Dalton, C. 2006 Effects of the corner radius on the near wake of a square prism. Exp. Fluids 40, 106–118.CrossRefGoogle Scholar
Hunt, J.C.R., Abell, C.J., Peterka, J.A. & Woo, H. 1978 Kinematical studies of the flows around free or surface-mounted obstacles; applying topology to flow visualization. J. Fluid Mech. 86, 179–200.CrossRefGoogle Scholar
Igarashi, T. 1984 Characteristics of the flow around a square prism. Bull. JSME 27 (231), 1858–1865.CrossRefGoogle Scholar
Inoue, O., Iwakami, W. & Hatakeyama, N. 2006 Aeolian tones radiated from flow past two square cylinders in a side-by-side arrangement. Phys. Fluids 18 (4), 046104.Google Scholar
Islam, M.R., Shaaban, M. & Mohany, A. 2020 Vortex dynamics and acoustic sources in the wake of finned cylinders during resonance excitation. Phys. Fluids 32 (7), 075117.CrossRefGoogle Scholar
Keefe, R.T. 1962 Investigation of the fluctuating forces acting on a stationary circular cylinder in a subsonic stream and of the associated sound field. J. Acoust. Soc. Am. 34 (11), 1711–1714.CrossRefGoogle Scholar
Knisely, C.W. 1990 Strouhal numbers of rectangular cylinders at incidence: a review and new data. J. Fluids Struct. 4 (4), 371–393.CrossRefGoogle Scholar
Kurtulus, D.F., Scarano, F. & David, L. 2007 Unsteady aerodynamic forces estimation on a square cylinder by TR-PIV. Exp. Fluids 42 (2), 185–196.CrossRefGoogle Scholar
Lyn, D.A., Einav, S., Rodi, W. & Park, J.-H. 1995 A laser-doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder. J. Fluid Mech. 304, 285–319.CrossRefGoogle Scholar
Lyn, D.A. & Rodi, W. 1994 The flapping shear layer formed by flow separation from the forward corner of a square cylinder. J. Fluid Mech. 267, 353–376.CrossRefGoogle Scholar
Mills, R., Sheridan, J. & Hourigan, K. 2003 Particle image velocimetry and visualization of natural and forced flow around rectangular cylinders. J. Fluid Mech. 478, 299–323.CrossRefGoogle Scholar
Mills, R., Sheridan, J., Hourigan, K. & Welsh, M.C. 1995 The mechanism controlling vortex shedding from rectangular bluff bodies. In Proceedings of the Twelfth Australasian Fluid Mechanics Conference, pp. 227–230. Sidney University Press.Google Scholar
Mohany, A., Arthurs, D., Bolduc, M., Hassan, M. & Ziada, S. 2014 Numerical and experimental investigation of flow-acoustic resonance of side-by-side cylinders in a duct. J. Fluids Struct. 48, 316–331.CrossRefGoogle Scholar
Mohany, A. & Ziada, S. 2005 Flow-excited acoustic resonance of two tandem cylinders in cross-flow. J. Fluids Struct. 21 (1), 103–119.CrossRefGoogle Scholar
Mohany, A. & Ziada, S. 2009 A parametric study of the resonance mechanism of two tandem cylinders in cross-flow. J. Press. Ves. Technol. 131 (2), 63–71.CrossRefGoogle Scholar
Nakamura, Y. & Nakashima, M. 1986 Vortex excitation of prisms with elongated rectangular, H and cross-sections. J. Fluid Mech. 163, 149–169.CrossRefGoogle Scholar
Nakamura, Y., Ohya, Y. & Tsuruta, H. 1991 Experiments on vortex shedding from flat plates with square leading and trailing edges. J. Fluid Mech. 222, 437–447.CrossRefGoogle Scholar
Naudascher, E. & Rockwell, D. 1994 Flow Induced Vibrations – An Engineering Guide. A. A. Balkema.Google Scholar
Okajima, A. 1982 Strouhal numbers of rectangular cylinders. J. Fluid Mech. 123, 379–398.CrossRefGoogle Scholar
van Oudheusden, B.W., Scarano, F., van Hinsberg, N.P. & Watt, D.W. 2005 Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 39, 86–98.CrossRefGoogle Scholar
Ozgoren, M. 2006 Flow structure in the downstream of square and circular cylinders. Flow Meas. Instrum. 17 (4), 225–235.CrossRefGoogle Scholar
Ozono, S., Ohya, Y., Nakamura, Y. & Nakayama, R. 1992 Stepwise increase in the Strouhal number for flows around flat plates. Intl J. Numer. Meth. Fluids 15 (9), 1025–1036.CrossRefGoogle Scholar
Parker, R. & Llewelyn, D. 1972 Flow induced vibration of cantilever mounted flat plates in an enclosed passage: an experimental investigation. J. Sound Vib. 25 (3), 451–463.CrossRefGoogle Scholar
Perrin, R., Braza, M., Cid, E., Cazin, S., Barthet, A., Sevrain, A., Mockett, C. & Thiele, F. 2007 Obtaining phase averaged turbulence properties in the near wake of a circular cylinder at high Reynolds number using POD. Exp. Fluids 43, 341–355.CrossRefGoogle Scholar
Prasanth, T.K. & Mittal, S. 2008 Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 594, 463–491.CrossRefGoogle Scholar
Raffel, M., Willert, C.E., Scarano, F., Kähler, C.J., Wereley, S.T. & Kompenhans, J. 2018 Particle Image Velocimetry: A Practical Guide. Springer.CrossRefGoogle Scholar
Rockwell, D.O. 1977 Organized fluctuations due to flow past a square cross section cylinder. Trans. ASME J. Fluids Engng 99 (3), 511–516.CrossRefGoogle Scholar
Saha, A., Muralidhar, K. & Biswas, G. 2000 a Experimental study of flow past a square cylinder at high Reynolds numbers. Exp. Fluids 29 (6), 553–563.CrossRefGoogle Scholar
Saha, A.K., Biswas, G. & Muralidhar, K. 2003 Three-dimensional study of flow past a square cylinder at low Reynolds numbers. Intl J. Heat Fluid Flow 24 (1), 54–66.CrossRefGoogle Scholar
Saha, A.K., Muralidhar, K. & Biswas, G. 2000 b Vortex structures and kinetic energy budget in two-dimensional flow past a square cylinder. Comput. Fluids 29, 669–694.CrossRefGoogle Scholar
Sarioglu, M., Akansu, Y.E. & Yavuz, T. 2005 Control of the flow around square cylinders at incidence by using a rod. AIAA J. 43 (7), 1419–1426.CrossRefGoogle Scholar
Shaaban, M. & Mohany, A. 2022 Flow–acoustic coupling around rectangular rods of different aspect ratios and incidence angles. Exp. Fluids 63, 45.CrossRefGoogle Scholar
Shoukry, A. & Mohany, A. 2023 Characteristics of the flow-induced noise from rectangular rods with different aspect ratios and edge geometry. J. Fluids Struct. 122, 103959.CrossRefGoogle Scholar
Singh, S.P. & Biswas, G. 2013 Vortex induced vibrations of a square cylinder at subcritical Reynolds numbers. J. Fluids Struct. 41, 146–155.CrossRefGoogle Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1998 Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition. Intl J. Numer. Meth. Fluids 26, 39–56.3.0.CO;2-P>CrossRefGoogle Scholar
Stokes, A.N. & Welsh, M.C. 1986 Flow-resonant sound interaction in a duct containing a plate. Part II. Square leading edge. J. Sound Vib. 104, 55–73.CrossRefGoogle Scholar
Tan, B.T., Thompson, M. & Hourigan, K. 1998 Simulated flow around long rectangular plates under cross flow perturbations. Intl J. Fluid Dyn. 2, 1.Google Scholar
Taneda, S. 1983 The main structure of turbulent boundary layers. J. Phys. Soc. Japan 52 (12), 4138–4144.CrossRefGoogle Scholar
Taylor, I. & Vezza, M. 1999 Prediction of unsteady flow around square and rectangular section cylinders using a discrete vortex method. J. Wind Engng Ind. Aerodyn. 82 (1), 247–269.CrossRefGoogle Scholar
Welsh, M.C. & Gibson, D.C. 1979 Interaction of induced sound with flow past a square leading edged plate in a duct. J. Sound Vib. 67 (4), 501–511.CrossRefGoogle Scholar
Zaki, T.G., Sen, M. & Gad-El-Hak, M. 1994 Numerical and experimental investigation of flow past a freely rotatable square cylinder. J. Fluids Struct. 8 (7), 555–582.CrossRefGoogle Scholar