Published online by Cambridge University Press: 28 September 2015
We present a numerical study on the self-induced flapping dynamics of an inverted flexible foil in a uniform flow. A high-order coupled fluid–structure solver based on fully coupled Navier–Stokes and nonlinear structural dynamic equations has been employed. Unlike a conventional flexible foil flapping where the leading edge is clamped, the inverted elastic foil is fixed at the trailing edge and the leading edge is allowed to oscillate freely. We investigate the evolution of flapping instability of an inverted foil as a function of the non-dimensional bending rigidity, 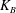 $K_{B}$, Reynolds number,
$K_{B}$, Reynolds number, 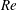 $\mathit{Re}$, and structure-to-fluid mass ratio,
$\mathit{Re}$, and structure-to-fluid mass ratio, 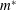 $m^{\ast }$, and identify three distinct stability regimes, namely (i) fixed-point stable, (ii) deformed steady and (iii) unsteady flapping state. With the aid of a simplified analytical model, we show that the fixed-point stable regime loses its stability by static-divergence instability. The transition from the deformed steady state to the unsteady flapping regime is marked by a flow separation at the leading edge. We also show that an inverted foil is more vulnerable to static divergence than a conventional foil. Three distinct unsteady flapping modes have been observed as a function of decreasing
$m^{\ast }$, and identify three distinct stability regimes, namely (i) fixed-point stable, (ii) deformed steady and (iii) unsteady flapping state. With the aid of a simplified analytical model, we show that the fixed-point stable regime loses its stability by static-divergence instability. The transition from the deformed steady state to the unsteady flapping regime is marked by a flow separation at the leading edge. We also show that an inverted foil is more vulnerable to static divergence than a conventional foil. Three distinct unsteady flapping modes have been observed as a function of decreasing 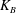 $K_{B}$: (i) inverted limit-cycle oscillations, (ii) deformed flapping and (iii) flipped flapping. We characterize the transition to the deformed-flapping regime through a quasistatic equilibrium analysis between the structural restoring and the fluid forces. We further examine the effects of
$K_{B}$: (i) inverted limit-cycle oscillations, (ii) deformed flapping and (iii) flipped flapping. We characterize the transition to the deformed-flapping regime through a quasistatic equilibrium analysis between the structural restoring and the fluid forces. We further examine the effects of 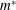 $m^{\ast }$ on the post-critical flapping dynamics at a fixed
$m^{\ast }$ on the post-critical flapping dynamics at a fixed 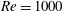 $\mathit{Re}=1000$. Finally, we present the net work done by the fluid and the bending strain energy developed in a flexible foil due to the flapping motion. For small
$\mathit{Re}=1000$. Finally, we present the net work done by the fluid and the bending strain energy developed in a flexible foil due to the flapping motion. For small 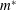 $m^{\ast }$, we demonstrate that the flapping of an inverted flexible foil can generate
$m^{\ast }$, we demonstrate that the flapping of an inverted flexible foil can generate 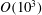 $O(10^{3})$ times more strain energy in comparison to a conventional flexible foil flapping, which has a profound impact on energy harvesting devices.
$O(10^{3})$ times more strain energy in comparison to a conventional flexible foil flapping, which has a profound impact on energy harvesting devices.