Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-08T04:11:34.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion

Published online by Cambridge University Press:  04 July 2014

Markus Uhlmann  and
Todor Doychev
Markus Uhlmann*
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
Todor Doychev
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

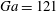Direct numerical simulation of the gravity-induced settling of finite-size particles in triply periodic domains has been performed under dilute conditions. For a single solid-to-fluid-density ratio of 1.5 we have considered two values of the Galileo number corresponding to steady vertical motion ($\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ga}=121$) and to steady oblique motion (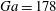$\mathit{Ga}=178$) in the case of one isolated sphere. For the multiparticle system we observe strong particle clustering only in the latter case. The geometry and time scales related to clustering are determined from Voronoï tessellation and particle-conditioned averaging. As a consequence of clustering, the average particle settling velocity is increased by 12 % as compared with the value of an isolated sphere; such a collective effect is not observed in the non-clustering case. By defining a local (instantaneous) fluid velocity average in the vicinity of the finite-size particles it is shown that the observed enhancement of the settling velocity is due to the fact that the downward fluid motion (with respect to the global average) which is induced in the cluster regions is preferentially sampled by the particles. It is further observed that the variance of the particle velocity is strongly enhanced in the clustering case. With the aid of a decomposition of the particle velocity it is shown that this increase is due to enhanced fluid velocity fluctuations (due to clustering) in the vicinity of the particles. Finally, we discuss a possible explanation for the observation of a critical Galileo number marking the onset of clustering under dilute conditions.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 310 - 348
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.CrossRefGoogle Scholar
Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.CrossRefGoogle Scholar
Beetstra, R., van der Hoef, M. A. & Kuipers, J. A. M. 2007 Drag force of intermediate Reynolds number flow past mono- and bidisperse arrays of spheres. AIChE J. 53 (2), 489–501.CrossRefGoogle Scholar
Bouchet, G., Mebarek, M. & Dušek, J. 2006 Hydrodynamic forces acting on a rigid fixed sphere in early transitional regimes. Eur. J. Mech. (B/Fluids) 25, 321–336.CrossRefGoogle Scholar
Cartellier, A., Andreotti, M. & Sechet, P. 2009 Induced agitation in homogeneous bubbly flows at moderate particle Reynolds number. Phys. Rev. E 80, 065301.CrossRefGoogle ScholarPubMed
Chan-Braun, C., García-Villalba, M. & Uhlmann, M. 2011 Force and torque acting on particles in a transitionally rough open channel flow. J. Fluid Mech. 684, 441–474.CrossRefGoogle Scholar
Chan-Braun, C., García-Villalba, M. & Uhlmann, M. 2013 Spatial and temporal scales of force and torque acting on wall-mounted spherical particles in open channel flow. Phys. Fluids 25 (7), 075103.CrossRefGoogle Scholar
Cisse, M., Homann, H. & Bec, J. 2013 Slipping motion of large neutrally buoyant particles in turbulence. J. Fluid Mech. 735, R3.CrossRefGoogle Scholar
Ferenc, J.-S. & Neda, Z. 2007 On the size distribution of Poisson Voronoi cells. Physica A 385, 518–526.CrossRefGoogle Scholar
Fessler, J. R., Kulick, J. D. & Eaton, J. K. 1994 Preferential concentration of heavy particles in a turbulent channel flow. Phys. Fluids 6 (11), 3742–3749.CrossRefGoogle Scholar
Fortes, A. F., Joseph, D. D. & Lundgren, T. S. 1987 Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 177, 467–483.CrossRefGoogle Scholar
García-Villalba, M., Kidanemariam, A. G. & Uhlmann, M. 2012 DNS of vertical plane channel flow with finite-size particles: Voronoi analysis, acceleration statistics and particle-conditioned averaging. Intl J. Multiphase Flow 46, 54–74.CrossRefGoogle Scholar
Ghidersa, B. & Dušek, J. 2000 Breaking of axisymmetry and onset of unsteadiness in the wake of a sphere. J. Fluid Mech. 423, 33–69.CrossRefGoogle Scholar
Glowinski, R., Pan, T.-W., Hesla, T. I. & Joseph, D. D. 1999 A distributed Lagrange multiplier/fictitious domain method for particulate flows. Intl J. Multiphase Flow 25, 755–794.CrossRefGoogle Scholar
Hill, R. J., Koch, D. L. & Ladd, A. J. C. 2001 Moderate-Reynolds-number flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 243–278.CrossRefGoogle Scholar
Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.CrossRefGoogle Scholar
Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
Kajishima, T. 2004 Influence of particle rotation on the interaction between particle clusters and particle-induced turbulence. Intl J. Heat Fluid Flow 25 (5), 721–728.CrossRefGoogle Scholar
Kajishima, T. & Takiguchi, S. 2002 Interaction between particle clusters and particle-induced turbulence. Intl J. Heat Fluid Flow 23, 639–646.CrossRefGoogle Scholar
Kidanemariam, A. G., Chan-Braun, C., Doychev, T. & Uhlmann, M. 2013 DNS of horizontal open channel flow with finite-size, heavy particles at low solid volume fraction. New J. Phys. 15 (2), 025031.CrossRefGoogle Scholar
Kim, I., Elghobashi, S. & Sirignano, W. A. 1993 Three-dimensional flow over two spheres placed side by side. J. Fluid Mech. 246, 465–488.CrossRefGoogle Scholar
Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly air–water flow. J. Fluid Mech. 222, 95–118.CrossRefGoogle Scholar
Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.CrossRefGoogle Scholar
Martinez-Mercado, J., Palacios-Morales, C. A. & Zenit, R. 2007 Measurement of pseudoturbulence intensity in monodispersed bubbly liquids for $10 < \mathit{Re} < 500$ . Phys. Fluids 19 (10), 103302.CrossRefGoogle Scholar
Melheim, J. A. 2005 Cluster integration method in Lagrangian particle dynamics. Comput. Phys. Commun. 171 (3), 155–161.CrossRefGoogle Scholar
Merle, A., Legendre, D. & Magnaudet, J. 2005 Forces on a high-Reynolds-number spherical bubble in a turbulent flow. J. Fluid Mech. 532, 53–62.CrossRefGoogle Scholar
Mizukami, M., Parthasarathy, R. N. & Faeth, G. M. 1992 Particle-generated turbulence in homogeneous dilute dispersed flows. Intl J. Multiphase Flow 18 (3), 397–412.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010a Inertial particles clustering in turbulent flows: a Voronoi analysis. In ICMF 2010 (ed. Balachandar, S. & Sinclair Curtis, J.). The University of Florida, CD-ROM.Google Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010b Preferential concentration of heavy particles: a Voronoï analysis. Phys. Fluids 22, 103304.CrossRefGoogle Scholar
Monchaux, R., Bourgoin, M. & Cartellier, A. 2012 Analyzing preferential concentration and clustering of inertial particles in turbulence. Intl J. Multiphase Flow 40, 1–18.CrossRefGoogle Scholar
Okabe, A., Boots, B., Sugihara, K. & Chiu, S. N. 1992 Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. Wiley.Google Scholar
Parthasarathy, R. N. & Faeth, G. M. 1990a Turbulence modulation in homogeneous dilute particle-laden flows. J. Fluid Mech. 220, 485–514.CrossRefGoogle Scholar
Parthasarathy, R. N. & Faeth, G. M. 1990b Turbulent dispersion of particles in self-generated homogeneous turbulence. J. Fluid Mech. 220, 515–537.CrossRefGoogle Scholar
Riboux, G., Legendre, D. & Risso, F. 2013 A model of bubble-induced turbulence based on large-scale wake interactions. J. Fluid Mech. 719, 362–387.CrossRefGoogle Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.CrossRefGoogle Scholar
Risso, F. 2011 Theoretical model for $k^{-3}$ spectra in dispersed multiphase flows. Phys. Fluids 23 (1), 011701.CrossRefGoogle Scholar
Risso, F. & Ellingsen, K. 2002 Velocity fluctuations in a homogeneous dilute dispersion of high-Reynolds-number rising bubbles. J. Fluid Mech. 453, 395–410.CrossRefGoogle Scholar
Risso, F., Roig, V., Amoura, Z., Riboux, G. & Billet, A.-M. 2008 Wake attenuation in large Reynolds number dispersed two-phase flows. Phil. Trans. R. Soc. A 366 (1873), 2177–2190.CrossRefGoogle ScholarPubMed
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C. M. 2012 Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.CrossRefGoogle Scholar
Schouveiler, L., Brydon, A., Leweke, T. & Thompson, M. C. 2004 Interactions of the wakes of two spheres placed side by side. Eur. J. Mech. (B/Fluids) 23 (1), 137–145.CrossRefGoogle Scholar
Schouveiler, L. & Provensal, M. 2002 Self-sustained oscillations in the wake of a sphere. Phys. Fluids 14 (11), 3846–3854.CrossRefGoogle Scholar
Shotorban, B. & Balachandar, S. 2006 Particle concentration in homogeneous shear turbulence simulated via Lagrangian and equilibrium Eulerian approaches. Phys. Fluids 18, 065105.CrossRefGoogle Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.CrossRefGoogle Scholar
Tennetti, S., Garg, R. & Subramaniam, S. 2011 Drag law for monodisperse gas–solid systems using particle-resolved direct numerical simulation of flow past fixed assemblies of spheres. Intl J. Multiphase Flow 37, 1072–1092.CrossRefGoogle Scholar
Tsuji, T., Narutomi, R., Yokomine, T., Ebara, S. & Shimizu, A. 2003 Unsteady three-dimensional simulation of interactions between flow and two particles. Intl J. Multiphase Flow 29 (9), 1431–1450.CrossRefGoogle Scholar
Tsuji, Y., Morikawa, Y. & Terashima, K. 1982 Fluid-dynamic interaction between two spheres. Intl J. Multiphase Flow 8 (1), 71–82.CrossRefGoogle Scholar
Uhlmann, M.2004 New results on the simulation of particulate flows. Technical Report No. 1038, CIEMAT, Madrid, Spain, ISSN 1135-9420.Google Scholar
Uhlmann, M. 2005a An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
Uhlmann, M. 2005b Proceedings of 11th Workshop Two-Phase Flow Predictions (Merseburg, Germany) (ed. Sommerfeld, M.), An improved fluid–solid coupling method for DNS of particulate flow on a fixed mesh. Universität Halle.Google Scholar
Uhlmann, M. 2006 Experience with DNS of particulate flow using a variant of the immersed boundary method. In Proceedings of ECCOMAS CFD 2006 (Egmond aan Zee, The Netherlands) (ed. Wesseling, P., Oñate, E. & Périaux, J.). TU Delft.Google Scholar
Uhlmann, M. 2008 Interface-resolved direct numerical simulation of vertical particulate channel flow in the turbulent regime. Phys. Fluids 20 (5), 053305.CrossRefGoogle Scholar
Uhlmann, M. & Dušek, J. 2014 The motion of a single heavy sphere in ambient fluid: a benchmark for interface-resolved particulate flow simulations with significant relative velocities. Intl J. Multiphase Flow 59, 221–243.CrossRefGoogle Scholar
Veldhuis, C. H. J. & Biesheuvel, A. 2007 An experimental study of the regimes of motion of spheres falling or ascending freely in a newtonian fluid. Intl J. Multiphase Flow 33 (10), 1074–1087.CrossRefGoogle Scholar
Wu, J. & Manasseh, R. 1998 Dynamics of dual-particles settling under gravity. Intl J. Multiphase Flow 24, 1343–1358.CrossRefGoogle Scholar
Wylie, J. J. & Koch, D. L. 2000 Particle clustering due to hydrodynamical interactions. Phys. Fluids 12 (5), 964–970.CrossRefGoogle Scholar
Yin, X. & Koch, D. L. 2008 Velocity fluctuations and hydrodynamic diffusion in finite-Reynolds-number sedimenting suspensions. Phys. Fluids 20 (4), 043305.CrossRefGoogle Scholar