Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-03T00:42:56.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Second-order sensitivity of parallel shear flows and optimal spanwise-periodic flow modifications

Published online by Cambridge University Press:  08 October 2015

E. Boujo ,
A. Fani  and
F. Gallaire
E. Boujo*
Affiliation:
LFMI, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland CAPS, ETH Zurich, CH-8092 Zurich, Switzerland
A. Fani
Affiliation:
LFMI, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland
F. Gallaire
Affiliation:
LFMI, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The question of optimal spanwise-periodic modification for the stabilisation of spanwise-invariant flows is addressed. A second-order sensitivity analysis is conducted for the linear temporal stability of parallel flows 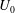$U_{0}$ subject to small-amplitude spanwise-periodic modification 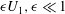${\it\epsilon}U_{1},{\it\epsilon}\ll 1$. It is known that spanwise-periodic flow modifications have a quadratic effect on stability properties, i.e. the first-order eigenvalue variation is zero, hence the need for a second-order analysis. A second-order sensitivity operator is computed from a one-dimensional calculation, which allows one to predict how eigenvalues are affected by any flow modification 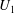$U_{1}$, without actually solving for modified eigenvalues and eigenmodes. Comparisons with full two-dimensional stability calculations in a plane channel flow and in a mixing layer show excellent agreement. Next, optimisation is performed on the second-order sensitivity operator: for each eigenmode streamwise wavenumber 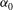${\it\alpha}_{0}$ and base flow modification spanwise wavenumber 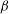${\it\beta}$, the most stabilising/destabilising profiles 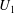$U_{1}$ are computed, together with lower/upper bounds for the variation in leading eigenvalue. These bounds increase like 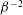${\it\beta}^{-2}$ as 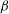${\it\beta}$ goes to zero, thus yielding a large stabilising potential. However, three-dimensional modes with wavenumbers 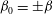${\it\beta}_{0}=\pm {\it\beta}$, 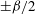$\pm {\it\beta}/2$ are destabilised, and therefore larger control wavenumbers should be preferred. The most stabilising 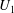$U_{1}$ optimised for the most unstable streamwise wavenumber 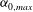${\it\alpha}_{0,max}$ has a stabilising effect on modes with other 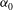${\it\alpha}_{0}$ values too. Finally, the potential of transient growth to amplify perturbations and stabilise the flow is assessed with a combined optimisation. Assuming a separation of time scales between the fast unstable mode and the slow transient evolution of the optimal perturbations, combined optimal perturbations that achieve the best balance between transient linear amplification and stabilisation of the nominal shear flow are determined. In the mixing layer with 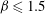${\it\beta}\leqslant 1.5$, these combined optimal perturbations appear similar to transient growth-only optimal perturbations, and achieve a more efficient overall stabilisation than optimal spanwise-periodic and spanwise-invariant modifications computed for stabilisation only. These results are consistent with the efficiency of streak-based control strategies.

JFM classification

Flow Control: Flow Control Instability: Instability Wakes/Jets: Shear layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , pp. 491 - 514
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Betchov, R. & Szewczyk, A. 1963 Stability of a shear layer between parallel streams. Phys. Fluids 6 (10), 1391–1396.CrossRefGoogle Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.Google Scholar
Butler, K. & Farrell, B. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4 (8), 1637–1650.Google Scholar
Choi, H., Jeon, W.-P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
Chomaz, J. M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Cossu, C.2014 On the stabilizing mechanism of 2D absolute and global instabilities by 3D streaks. ArXiv e-prints, arXiv:1404.3191.Google Scholar
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14 (8), L57–L60.Google Scholar
Cossu, C. & Brandt, L. 2004 On Tollmien–Schlichting-like waves in streaky boundary layers. Eur. J. Mech. (B/Fluids) 23 (6), 815–833.Google Scholar
Del Guercio, G., Cossu, C. & Pujals, G. 2014 Stabilizing effect of optimally amplified streaks in parallel wakes. J. Fluid Mech. 739, 37–56.CrossRefGoogle Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilization of Tollmien–Schlichting waves by finite amplitude streaks. Phys. Fluids 17 (5), 054110.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Hecht, F. 2012 New development in FreeFem++. J. Numer. Math. 20 (3–4), 251–265.CrossRefGoogle Scholar
Herbert, T. 1988 Secondary instability of boundary layers. Annu. Rev. Fluid Mech. 20 (1), 487–526.CrossRefGoogle Scholar
Hernandez, V., Roman, J. E. & Vidal, V. 2005 SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 31 (3), 351–362.Google Scholar
Hill, D. C. 1992 A theoretical approach for analyzing the restabilization of wakes. AIAA 92-0067.Google Scholar
Hinch, E. 1991 Perturbation Methods. Cambridge University Press.CrossRefGoogle Scholar
Hwang, Y., Kim, J. & Choi, H. 2013 Stabilization of absolute instability in spanwise wavy two-dimensional wakes. J. Fluid Mech. 727, 346–378.Google Scholar
Kim, J. & Choi, H. 2005 Distributed forcing of flow over a circular cylinder. Phys. Fluids 17 (3), 033103.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Meliga, P., Sipp, D. & Chomaz, J.-M. 2010 Open-loop control of compressible afterbody flows using adjoint methods. Phys. Fluids 22 (5), 054109.CrossRefGoogle Scholar
Michalke, A. 1964 On the inviscid instability of the hyperbolic-tangent velocity profile. J. Fluid Mech. 19, 543–556.Google Scholar
Reddy, S. C., Schmid, P. J., Baggett, J. S. & Henningson, D. S. 1998 On stability of streamwise streaks and transition thresholds in plane channel flows. J. Fluid Mech. 365, 269–303.Google Scholar
Schmid, P. & Henningson, D. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Tammisola, O., Giannetti, F., Citro, V. & Juniper, M. P. 2014 Second-order perturbation of global modes and implications for spanwise wavy actuation. J. Fluid Mech. 755, 314–335.CrossRefGoogle Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.Google Scholar
Villermaux, E. 1998 On the role of viscosity in shear instabilities. Phys. Fluids 10 (2), 368–373.CrossRefGoogle Scholar
Zdravkovich, M. 1981 Review and classification of various aerodynamic and hydrodynamic means for suppressing vortex shedding. J. Wind Engng Ind. Aerodyn. 7 (2), 145–189.CrossRefGoogle Scholar