Article contents
Secondary instabilities in the wake of an elongated two-dimensional body with a blunt trailing edge
Published online by Cambridge University Press: 08 May 2018
Abstract
The secondary instability in the wake of a two-dimensional blunt body with a chord to thickness ratio of 46.5 was experimentally investigated for Reynolds numbers of 3500, 5200 and 7000 based on the blunt trailing edge height
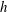 $h$
. Planar, stereoscopic and high-speed particle image velocimetry (PIV) measurements were performed to characterise the wake and upstream boundary layer. The same mode B secondary instability that is found in the cylinder wake was found to be present in the wake of the elongated body studied here. The most probable wavelength of the secondary instability, defined as the spanwise distance between adjacent streamwise vortex pairs in the wake, was found to range from
$h$
. Planar, stereoscopic and high-speed particle image velocimetry (PIV) measurements were performed to characterise the wake and upstream boundary layer. The same mode B secondary instability that is found in the cylinder wake was found to be present in the wake of the elongated body studied here. The most probable wavelength of the secondary instability, defined as the spanwise distance between adjacent streamwise vortex pairs in the wake, was found to range from
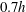 $0.7h$
to
$0.7h$
to
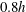 $0.8h$
by applying a spatial autocorrelation to the spanwise–wall-normal instantaneous fields of the
$0.8h$
by applying a spatial autocorrelation to the spanwise–wall-normal instantaneous fields of the
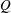 $Q$
-criterion. The temporal evolution of the secondary wake vortices was investigated using time-resolved stereoscopic PIV measurements and it was shown that the vortices maintain both their directions of rotation and spanwise positions during the primary vortex shedding cycles. In agreement with previous literature, the secondary instability did not greatly change as the upstream boundary layer transitioned from laminar to turbulent. Moreover, any upstream boundary layer structures were found to rapidly evolve into wake structures just past the blunt trailing edge. The wavelength of the secondary instability was shown to match the spanwise distance between adjacent low-speed zones of streamwise velocity in the wake. These undulating velocity patterns proved to be a viable method for determining the secondary instability wavelength; however, this type of analysis is highly sensitive to the energy content used for data reconstruction when proper orthogonal decomposition is applied beforehand.
$Q$
-criterion. The temporal evolution of the secondary wake vortices was investigated using time-resolved stereoscopic PIV measurements and it was shown that the vortices maintain both their directions of rotation and spanwise positions during the primary vortex shedding cycles. In agreement with previous literature, the secondary instability did not greatly change as the upstream boundary layer transitioned from laminar to turbulent. Moreover, any upstream boundary layer structures were found to rapidly evolve into wake structures just past the blunt trailing edge. The wavelength of the secondary instability was shown to match the spanwise distance between adjacent low-speed zones of streamwise velocity in the wake. These undulating velocity patterns proved to be a viable method for determining the secondary instability wavelength; however, this type of analysis is highly sensitive to the energy content used for data reconstruction when proper orthogonal decomposition is applied beforehand.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Gibeau et al. supplementary movie 1
An animations of the streamwise vortices measured by Stereo-PIV in the zy plane of the wake at Re(h)=3500.
- 14
- Cited by



