Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T09:04:14.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Secondary flow in spanwise-periodic in-phase sinusoidal channels

Published online by Cambridge University Press:  19 July 2018

A. Vidal Open the ORCID record for A. Vidal [Opens in a new window] ,
H. M. Nagib ,
P. Schlatter Open the ORCID record for P. Schlatter [Opens in a new window]  and
R. Vinuesa Open the ORCID record for R. Vinuesa [Opens in a new window]
A. Vidal*
Affiliation:
Department of MMAE, Illinois Institute of Technology, Chicago, IL 60616, USA
H. M. Nagib
Affiliation:
Department of MMAE, Illinois Institute of Technology, Chicago, IL 60616, USA
P. Schlatter
Affiliation:
Linné FLOW Centre, KTH Mechanics SE-100 44, Stockholm, Sweden Swedish e-Science Research Centre (SeRC), Stockholm, Sweden
R. Vinuesa
Affiliation:
Linné FLOW Centre, KTH Mechanics SE-100 44, Stockholm, Sweden Swedish e-Science Research Centre (SeRC), Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNSs) are performed to analyse the secondary flow of Prandtl’s second kind in fully developed spanwise-periodic channels with in-plane sinusoidal walls. The secondary flow is characterized for different combinations of wave parameters defining the wall geometry at 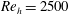$Re_{h}=2500$ and 5000, where 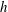$h$ is the half-height of the channel. The total cross-flow rate in the channel 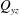$Q_{yz}$ is defined along with a theoretical model to predict its behaviour. Interaction between the secondary flows from opposite walls is observed if 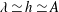$\unicode[STIX]{x1D706}\simeq h\simeq A$, where 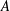$A$ and 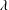$\unicode[STIX]{x1D706}$ are the amplitude and wavelength of the sinusoidal function defining the wall geometry. As the outer-scaled wavelength (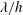$\unicode[STIX]{x1D706}/h$) is reduced, the secondary vortices become smaller and faster, increasing the total cross-flow rate per wall. However, if the inner-scaled wavelength (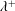$\unicode[STIX]{x1D706}^{+}$) is below 130 viscous units, the cross-flow decays for smaller wavelengths. By analysing cases in which the wavelength of the wall is much smaller than the half-height of the channel 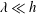$\unicode[STIX]{x1D706}\ll h$, we show that the cross-flow distribution depends almost entirely on the separation between the scales of the instantaneous vortices, where the upper and lower bounds are determined by 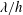$\unicode[STIX]{x1D706}/h$ and 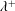$\unicode[STIX]{x1D706}^{+}$, respectively. Therefore, the distribution of the secondary flow relative to the size of the wave at a given 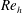$Re_{h}$ can be replicated at higher 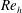$Re_{h}$ by decreasing 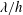$\unicode[STIX]{x1D706}/h$ and keeping 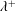$\unicode[STIX]{x1D706}^{+}$ constant. The mechanisms that contribute to the mean cross-flow are analysed in terms of the Reynolds stresses and using quadrant analysis to evaluate the probability density function of the bursting events. These events are further classified with respect to the sign of their instantaneous spanwise velocities. Sweeping events and ejections are preferentially located in the valleys and peaks of the wall, respectively. The sweeps direct the instantaneous cross-flow from the core of the channel towards the wall, turning in the wall-tangent direction towards the peaks. The ejections drive the instantaneous cross-flow from the near-wall region towards the core. This preferential behaviour is identified as one of the main contributors to the secondary flow.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 288 - 316
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Coceal, O. & Belcher, S. E. 2004 A canopy model of mean winds through urban areas. Q. J. R. Meteorol. Soc. 130, 1349–1372.Google Scholar
El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91, 475–495.Google Scholar
Farano, M., Cherubini, S., Robinet, J. C. & De Palma, P. 2017 Optimal bursts in turbulent channel flow. J. Fluid Mech. 817, 35–60.Google Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 NEK5000: open source spectral element CFD solver. Available at: http://nek5000.mcs.anl.gov.Google Scholar
García-Mayoral, R. & Jiménez, J. 2011 Drag reduction by riblets. Phil. Trans. R. Soc. Lond. A 369, 1412–1427.Google Scholar
Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.Google Scholar
Gessner, F. B. 1973 The origin of secondary flow in turbulent flow along a corner. J. Fluid Mech. 58, 1–25.Google Scholar
Goldstein, D. B. & Tuan, T.-C. 1998 Secondary flow induced by riblets. J. Fluid Mech. 363, 115–151.Google Scholar
Gupta, A. K., Laufer, J. & Kaplan, R. E. 1971 Spatial structure in the viscous sublayer. J. Fluid Mech. 50, 493–512.Google Scholar
Hosseini, S. M., Vinuesa, R., Schlatter, P., Hanifi, A. & Henningson, D. S. 2016 Direct numerical simulation of the flow around a wing section at moderate Reynolds number. Intl J. Heat Fluid Flow 61, 117–128.Google Scholar
Huser, A. & Biringen, S. 1993 Direct numerical simulation of turbulent flow in a square duct. J. Fluid Mech. 257, 65–95.Google Scholar
Jelly, T. O., Jung, S. Y. & Zaki, T. A. 2014 Turbulence and skin friction modification in channel flow with streamwise-aligned superhydrophobic surface texture. Phys. Fluids 26, 095102.Google Scholar
Jiménez, J., del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.Google Scholar
Jiménez, J. P. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Kim, J. 1985 Turbulence structures associated with the bursting event. Phys. Fluids 28, 52–58.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≃ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26, 011702.Google Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.Google Scholar
Maday, Y. & Patera, A. T. 1989 Spectral element methods for the Navier–Stokes equations. In State of the Art Surveys in Computational Mechanics (ed. Noor, A. K.), pp. 71–143. ASME.Google Scholar
Marin, O., Vinuesa, R., Obabko, A. V. & Schlatter, P. 2016 Characterization of the secondary flow in hexagonal ducts. Phys. Fluids 28, 125101.Google Scholar
Moinuddin, K. A. M., Joubert, P. N. & Chong, M. S. 2004 Experimental investigation of turbulence-driven secondary motion over a streamwise external corner. J. Fluid Mech. 511, 1–23.Google Scholar
Nikitin, N. & Yakhot, A. 2005 Direct numerical simulation of turbulent flow in elliptical ducts. J. Fluid Mech. 532, 141–164.Google Scholar
Panton, R. L. 1996 Incompressible Flow, 2nd edn, pp. 213–216. Wiley-Interscience.Google Scholar
Patera, A. T. 1984 A spectral element method for fluid dynamics: laminar flow in a channel expansion. J. Comput. Phys. 54, 468–488.Google Scholar
Perkins, H. J. 1970 The formation of streamwise vorticity in turbulent flow. J. Fluid Mech. 44, 721–740.Google Scholar
Pinelli, A., Uhlmann, M., Sekimoto, A. & Kawahara, G. 2010 Reynolds number dependence of mean flow structure in square duct turbulence. J. Fluid Mech. 644, 107–122.Google Scholar
Pope, S. B. 2000 Turbulent Flows, p. 2020. Cambridge University Press.Google Scholar
Prandtl, L. 1926 Über die ausgebildete Turbulenz. In Verh. 2nd Intl Kong. NACA Tech. Memo 62, 2nd Intl Kong. für Tech. Mech., Zürich, p. 435.Google Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers. Inflow length and tripping effects. J. Fluid Mech. 710, 5–34.Google Scholar
Spalart, P. R. 2000 Strategies for turbulence modelling and simulations. Intl J. Heat Fluid Flow 21, 252–263.Google Scholar
Uhlmann, M., Pinelli, A., Kawahara, G. & Sekimoto, A. 2007 Marginally turbulent flow in a square duct. J. Fluid Mech. 588, 153–162.Google Scholar
Vidal, A., Vinuesa, R., Schlatter, P. & Nagib, H. M. 2017 Influence of corner geometry on the secondary flow in turbulent square ducts. Intl J. Heat Fluid Flow 67, 69–78.Google Scholar
Vidal, A., Vinuesa, R., Schlatter, P. & Nagib, H. M. 2018 Turbulent rectangular ducts with minimum secondary flow. Intl J. Heat Fluid Flow 72, 317–328.Google Scholar
Vinuesa, R., Noorani, A., Lozano-Durán, A., El Khoury, G. K., Schlatter, P., Fischer, P. F. & Nagib, H. M. 2014 Aspect ratio effects in turbulent duct flows studied through direct numerical simulation. J. Turbul. 15, 677–706.Google Scholar
Vinuesa, R., Prus, C., Schlatter, P. & Nagib, H. M. 2016 Convergence of numerical simulations of turbulent wall-bounded flows and mean cross-flow structure of rectangular ducts. Meccanica 51, 3025–3042.Google Scholar
Vinuesa, R., Schlatter, P. & Nagib, H. M. 2015 On minimum aspect ratio for duct flow facilities and the role of side walls in generating secondary flows. J. Turbul. 16, 588–606.Google Scholar
Vinuesa, R., Schlatter, P. & Nagib, H. M. 2018 Secondary flow in turbulent ducts with increasing aspect ratio. Phys. Rev. Fluids 3, 054606.Google Scholar
Voronova, T. V. & Nikitin, N. 2006 Direct numerical simulation of the turbulent flow in an elliptical pipe. Comput. Math. Math. Phys. 46, 1378–1386.Google Scholar
Weatheritt, A. & Sandberg, R. 2016 A novel evolutionary algorithm to algebraic modications of the RANS stress–strain relationship. J. Comput. Phys. 325, 22–37.Google Scholar
Zhang, H., Trias, F. X., Gorobets, A., Tan, Y. & Oliva, A. 2015 Direct numerical simulation of a fully developed turbulent square duct flow up to Re 𝜏 = 1200. Intl J. Heat Fluid Flow 54, 258–267.Google Scholar