Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T06:54:38.641Z Has data issue: false hasContentIssue false
  • English
  • Français

School cohesion, speed and efficiency are modulated by the swimmers flapping motion

Published online by Cambridge University Press:  13 July 2021

Sina Heydari Open the ORCID record for Sina Heydari [Opens in a new window]  and
Eva Kanso Open the ORCID record for Eva Kanso [Opens in a new window]
Sina Heydari
Affiliation:
Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA90089, USA
Eva Kanso*
Affiliation:
Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA90089, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

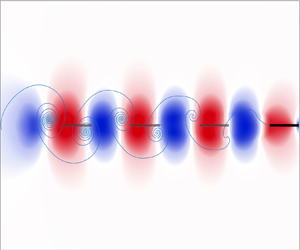
Fish schools are ubiquitous in marine life. Although flow interactions are thought to be beneficial for schooling, their exact effects on the speed, energetics and stability of the group remain elusive. Recent numerical simulations and experimental models suggest that flow interactions stabilize in-tandem formations of flapping foils. Here, we employ a minimal vortex sheet model that captures salient features of the flow interactions among flapping swimmers, and we study the free swimming of a pair of in-line swimmers driven with identical heaving or pitching motions. We find that, independent of the flapping mode, heaving or pitching, the follower passively stabilizes at discrete locations in the wake of the leader, consistent with the heaving foil experiments, but pitching swimmers exhibit tighter and more cohesive formations. Further, in comparison to swimming alone, pitching motions increase the energetic efficiency of the group while heaving motions result in a slight increase in the swimming speed. A deeper analysis of the wake of a single swimmer sheds light on the hydrodynamic mechanisms underlying pairwise formations. These results recapitulate that flow interactions provide a passive mechanism that promotes school cohesion, and afford novel insights into the role of the flapping mode in controlling the emergent properties of the school.

JFM classification

Biological Fluid Dynamics: Swimming/flying Nonlinear Dynamical Systems: Low-dimensional models Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 922 , 10 September 2021 , A27
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abrahams, M.V. & Colgan, P.W. 1985 Risk of predation, hydrodynamic efficiency and their influence on school structure. Environ. Biol. Fishes 13 (3), 195–202.CrossRefGoogle Scholar
Alben, S. 2009 Wake-mediated synchronization and drafting in coupled flags. J. Fluid Mech. 641, 489.CrossRefGoogle Scholar
Alben, S. & Shelley, M.J. 2008 Flapping states of a flag in an inviscid fluid: bistability and the transition to chaos. Phys. Rev. Lett. 100 (7), 074301.CrossRefGoogle Scholar
Ayancik, F., Fish, F.E. & Moored, K.W. 2020 Three-dimensional scaling laws of cetacean propulsion characterize the hydrodynamic interplay of flukes’ shape and kinematics. J. R. Soc. Interface 17 (163), 20190655.CrossRefGoogle ScholarPubMed
Beal, D.N., Hover, F.S., Triantafyllou, M.S., Liao, J.C. & Lauder, G.V. 2006 Passive propulsion in vortex wakes. J. Fluid Mech. 549, 385–402.CrossRefGoogle Scholar
Becker, A.D., Masoud, H., Newbolt, J.W., Shelley, M.J. & Ristroph, L. 2015 Hydrodynamic schooling of flapping swimmers. Nat. Commun. 6, 8514.CrossRefGoogle ScholarPubMed
Blondeaux, P., Fornarelli, F., Guglielmini, L., Triantafyllou, M.S. & Verzicco, R. 2005 Numerical experiments on flapping foils mimicking fish-like locomotion. Phys. Fluids 17 (11), 113601.CrossRefGoogle Scholar
Borazjani, I. 2008 Numerical Simulations of Fluid-Structure Interaction Problems in Biological Flows. University of Minnesota.Google Scholar
Buchholz, J.H.J. & Smits, A.J. 2008 The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.CrossRefGoogle ScholarPubMed
Dabiri, J.O. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41, 17–33.CrossRefGoogle Scholar
Dai, L., He, G., Zhang, X. & Zhang, X. 2018 Stable formations of self-propelled fish-like swimmers induced by hydrodynamic interactions. J. R. Soc. Interface 15 (147), 20180490.CrossRefGoogle ScholarPubMed
Dong, H., Mittal, R. & Najjar, F.M. 2006 Wake topology and hydrodynamic performance of low-aspect-ratio flapping foils. J. Fluid Mech. 566, 309–343.CrossRefGoogle Scholar
Eldredge, J.D. 2019 Mathematical Modeling of Unsteady Inviscid Flows. Springer.CrossRefGoogle Scholar
Fang, F. 2016 Hydrodynamic interactions between self-propelled flapping wings. PhD thesis, New York University.Google Scholar
Filella, A., Nadal, F., Sire, C., Kanso, E. & Eloy, C. 2018 Model of collective fish behavior with hydrodynamic interactions. Phys. Rev. Lett. 120 (19), 198101.CrossRefGoogle ScholarPubMed
Floryan, D., Van Buren, T., Rowley, C.W. & Smits, A.J. 2017 Scaling the propulsive performance of heaving and pitching foils. J. Fluid Mech. 822, 386–397.CrossRefGoogle Scholar
Franck, J.A. & Breuer, K.S. 2017 Unsteady high-lift mechanisms from heaving flat plate simulations. Intl J. Heat Fluid Flow 67, 230–239.CrossRefGoogle Scholar
Garrick, I.E., et al. 1937 Propulsion of a flapping and oscillating airfoil. NACA Rep. 567, 419–427.Google Scholar
Gazzola, M., Tchieu, A.A., Alexeev, D., de Brauer, A. & Koumoutsakos, P. 2016 Learning to school in the presence of hydrodynamic interactions. J. Fluid Mech. 789, 726–749.CrossRefGoogle Scholar
Huang, Y., Nitsche, M. & Kanso, E. 2016 Hovering in oscillatory flows. J. Fluid Mech. 804, 531–549.CrossRefGoogle Scholar
Huang, Y., Ristroph, L., Luhar, M. & Kanso, E. 2018 Bistability in the rotational motion of rigid and flexible flyers. J. Fluid Mech. 849, 1043–1067.CrossRefGoogle Scholar
Jones, M.A. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.CrossRefGoogle Scholar
Jones, M.A. & Shelley, M.J. 2005 Falling cards. J. Fluid Mech. 540, 393–425.CrossRefGoogle Scholar
Jusufi, A., Vogt, D.M., Wood, R.J. & Lauder, G.V. 2017 Undulatory swimming performance and body stiffness modulation in a soft robotic fish-inspired physical model. Soft Robot. 4 (3), 202–210.CrossRefGoogle Scholar
Kanso, E. & Newton, P.K. 2009 Passive locomotion via normal-mode coupling in a submerged spring-mass system. J. Fluid Mech. 641, 205–215.CrossRefGoogle Scholar
Kanso, E. & Tsang, A.C.H. 2014 Dipole models of self-propelled bodies. Fluid Dyn. Res. 46 (6), 061407.CrossRefGoogle Scholar
Kanso, E. & Tsang, A.C.H. 2015 Pursuit and synchronization in hydrodynamic dipoles. J. Nonlinear Sci. 25 (5), 1141.CrossRefGoogle Scholar
Lauder, G.V., Lim, J., Shelton, R., Witt, C., Anderson, E. & Tangorra, J.L. 2011 Robotic models for studying undulatory locomotion in fishes. Mar. Technol. Soc. J. 45 (4), 41–55.CrossRefGoogle Scholar
Liao, J.C. 2007 A review of fish swimming mechanics and behaviour in altered flows. Phil. Trans. R. Soc. B: Biol. Sci. 362 (1487), 1973–1993.CrossRefGoogle ScholarPubMed
Liao, J.C., Beal, D.N., Lauder, G.V. & Triantafyllou, M.S. 2003 Fish exploiting vortices decrease muscle activity. Science 302 (5650), 1566–1569.CrossRefGoogle ScholarPubMed
Lin, X., Wu, J. & Zhang, T. 2019 Performance investigation of a self-propelled foil with combined oscillating motion in stationary fluid. Ocean Engng 175, 33–49.CrossRefGoogle Scholar
Lin, X., Wu, J., Zhang, T. & Yang, L. 2020 Self-organization of multiple self-propelling flapping foils: energy saving and increased speed. J. Fluid Mech. 884, R1.CrossRefGoogle Scholar
Lucas, K.N., Johnson, N., Beaulieu, W.T., Cathcart, E., Tirrell, G., Colin, S.P., Gemmell, B.J., Dabiri, J.O. & Costello, J.H. 2014 Bending rules for animal propulsion. Nat. Commun. 5 (1), 3293.CrossRefGoogle ScholarPubMed
Marras, S., Killen, S.S., Lindström, J., McKenzie, D.J., Steffensen, J.F. & Domenici, P. 2015 Fish swimming in schools save energy regardless of their spatial position. Behav. Ecol. Sociobiol. 69 (2), 219–226.CrossRefGoogle ScholarPubMed
Moored, K.W. & Quinn, D.B. 2019 Inviscid scaling laws of a self-propelled pitching airfoil. AIAA J. 57 (9), 3686–3700.CrossRefGoogle Scholar
Newbolt, J.W., Zhang, J. & Ristroph, L. 2019 Flow interactions between uncoordinated flapping swimmers give rise to group cohesion. Proc. Natl Acad. Sci. 116, 201816098.CrossRefGoogle ScholarPubMed
Nitsche, M. & Krasny, R. 1994 A numerical study of vortex ring formation at the edge of a circular tube. J. Fluid Mech. 276, 139–161.CrossRefGoogle Scholar
Oza, A.U., Ristroph, L. & Shelley, M.J. 2019 Lattices of hydrodynamically interacting flapping swimmers. Phys. Rev. X 9 (4), 041024.Google Scholar
Park, S.G. & Sung, H.J. 2018 Hydrodynamics of flexible fins propelled in tandem, diagonal, triangular and diamond configurations. J. Fluid Mech. 840, 154–189.CrossRefGoogle Scholar
Partridge, B.L. 1982 The structure and function of fish schools. Sci. Am. 246 (6), 114–123.CrossRefGoogle ScholarPubMed
Partridge, B.L. & Pitcher, T.J. 1979 Evidence against a hydrodynamic function for fish schools. Nature 279 (5712), 418–419.CrossRefGoogle ScholarPubMed
Peng, Z.-R., Huang, H. & Xi-Yun, L. 2018 Collective locomotion of two closely spaced self-propelled flapping plates. J. Fluid Mech. 849, 1068–1095.CrossRefGoogle Scholar
Quinn, D.B., Lauder, G.V. & Smits, A.J. 2014 Scaling the propulsive performance of heaving flexible panels. J. Fluid Mech. 738, 250–267.CrossRefGoogle Scholar
Ramananarivo, S., Fang, F., Oza, A., Zhang, J. & Ristroph, L. 2016 Flow interactions lead to orderly formations of flapping wings in forward flight. Phys. Rev. Fluids 1, 071201.CrossRefGoogle Scholar
Saffman, P.G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Shaw, E. 1978 Schooling fishes: the school, a truly egalitarian form of organization in which all members of the group are alike in influence, offers substantial benefits to its participants. Am. Sci. 66 (2), 166–175.Google Scholar
Sheng, J.X., Ysasi, A., Kolomenskiy, D., Kanso, E., Nitsche, M. & Schneider, K. 2012 Simulating vortex wakes of flapping plates. In Natural Locomotion in Fluids and on Surfaces (ed. S. Childress, A. Hosoi, W.W. Schultz & J. Wang), pp. 255–262. Springer.CrossRefGoogle Scholar
Smits, A.J. 2019 Undulatory and oscillatory swimming. J. Fluid Mech. 874, P1.CrossRefGoogle Scholar
Taneda, S. 1965 Experimental investigation of vortex streets. J. Phys. Soc. Japan 20 (9), 1714–1721.CrossRefGoogle Scholar
Tchieu, A.A., Kanso, E. & Newton, P.K. 2012 The finite-dipole dynamical system. Proc. R. Soc. A: Math. Phys. Engng Sci. 468 (2146), 3006–3026.CrossRefGoogle Scholar
Triantafyllou, G.S., Triantafyllou, M.S. & Grosenbaugh, M.A. 1993 Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 7 (2), 205–224.CrossRefGoogle Scholar
Triantafyllou, M.S., Triantafyllou, G.S. & Yue, D.K. 2000 Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32 (1), 33–53.CrossRefGoogle Scholar
Tsang, A.C.H. & Kanso, E. 2013 Dipole interactions in doubly periodic domains. J. Nonlinear Sci. 23 (6), 971–991.CrossRefGoogle Scholar
Van Buren, T., Floryan, D. & Smits, A.J. 2019 Scaling and performance of simultaneously heaving and pitching foils. AIAA J. 57 (9), 3666–3677.CrossRefGoogle Scholar
Verma, S., Novati, G. & Koumoutsakos, P. 2018 Efficient collective swimming by harnessing vortices through deep reinforcement learning. Proc. Natl Acad. Sci. 115 (23), 5849–5854.CrossRefGoogle ScholarPubMed
Weihs, D. 1973 Hydromechanics of fish schooling. Nature 241, 241290a0.CrossRefGoogle Scholar
Weihs, D. 1975 Some hydrodynamical aspects of fish schooling. In Swimming and Flying in Nature, pp. 703–718. Springer.CrossRefGoogle Scholar
Wen, L. & Lauder, G. 2013 Understanding undulatory locomotion in fishes using an inertia-compensated flapping foil robotic device. Bioinspir. Biomim. 8 (4), 046013.CrossRefGoogle ScholarPubMed
White, F.M. 1979 Fluid Mechanics. Tata McGraw-Hill Education.Google Scholar
Wolfgang, M.J., Anderson, J.M., Grosenbaugh, M.A., Yue, D.K. & Triantafyllou, M.S. 1999 Near-body flow dynamics in swimming fish. J. Expl Biol. 202 (17), 2303–2327.CrossRefGoogle ScholarPubMed
Wu, T. 1971 Hydromechanics of swimming propulsion. Part 1. Swimming of a two-dimensional flexible plate at variable forward speeds in an inviscid fluid. J. Fluid Mech. 46 (2), 337–355.CrossRefGoogle Scholar
Zhu, X., He, G. & Zhang, X. 2014 Flow-mediated interactions between two self-propelled flapping filaments in tandem configuration. Phys. Rev. Lett. 113 (23), 238105.CrossRefGoogle ScholarPubMed

Heydari and Kanso supplementary movie

Flow interactions in pairs of heaving, pitching, and simultaneously heaving and pitching swimmers lead to stable formations

Download Heydari and Kanso supplementary movie(Video)
Video 7.7 MB