Published online by Cambridge University Press: 16 December 2016
We propose a new similarity theory for the two-dimensional inverse energy cascade and the coherent vortex population it contains when forced at intermediate scales. Similarity arguments taking into account enstrophy conservation and a prescribed constant energy injection rate such that 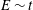 $E\sim t$ yield three length scales,
$E\sim t$ yield three length scales, 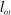 $l_{\unicode[STIX]{x1D714}}$,
$l_{\unicode[STIX]{x1D714}}$, 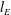 $l_{E}$ and
$l_{E}$ and 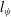 $l_{\unicode[STIX]{x1D713}}$, associated with the vorticity field, energy peak and streamfunction, and predictions for their temporal evolutions,
$l_{\unicode[STIX]{x1D713}}$, associated with the vorticity field, energy peak and streamfunction, and predictions for their temporal evolutions, 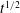 $t^{1/2}$,
$t^{1/2}$,  $t$ and
$t$ and  $t^{3/2}$, respectively. We thus predict that vortex areas grow linearly in time,
$t^{3/2}$, respectively. We thus predict that vortex areas grow linearly in time, 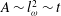 $A\sim l_{\unicode[STIX]{x1D714}}^{2}\sim t$, while the spectral peak wavenumber
$A\sim l_{\unicode[STIX]{x1D714}}^{2}\sim t$, while the spectral peak wavenumber 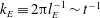 $k_{E}\equiv 2\unicode[STIX]{x03C0}l_{E}^{-1}\sim t^{-1}$. We construct a theoretical framework involving a three-part, time-evolving vortex number density distribution,
$k_{E}\equiv 2\unicode[STIX]{x03C0}l_{E}^{-1}\sim t^{-1}$. We construct a theoretical framework involving a three-part, time-evolving vortex number density distribution, 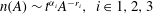 $n(A)\sim t^{\unicode[STIX]{x1D6FC}_{i}}A^{-r_{i}},~i\in 1,2,3$. Just above the forcing scale (
$n(A)\sim t^{\unicode[STIX]{x1D6FC}_{i}}A^{-r_{i}},~i\in 1,2,3$. Just above the forcing scale (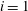 $i=1$) there is a forcing-equilibrated scaling range in which the number of vortices at fixed
$i=1$) there is a forcing-equilibrated scaling range in which the number of vortices at fixed 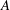 $A$ is constant and vortex ‘self-energy’
$A$ is constant and vortex ‘self-energy’ 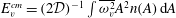 $E_{v}^{cm}=(2{\mathcal{D}})^{-1}\int \overline{\unicode[STIX]{x1D714}_{v}^{2}}A^{2}n(A)\,\text{d}A$ is conserved in
$E_{v}^{cm}=(2{\mathcal{D}})^{-1}\int \overline{\unicode[STIX]{x1D714}_{v}^{2}}A^{2}n(A)\,\text{d}A$ is conserved in 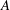 $A$-space intervals
$A$-space intervals 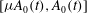 $[\unicode[STIX]{x1D707}A_{0}(t),A_{0}(t)]$ comoving with the growth in vortex area,
$[\unicode[STIX]{x1D707}A_{0}(t),A_{0}(t)]$ comoving with the growth in vortex area, 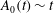 $A_{0}(t)\sim t$. In this range,
$A_{0}(t)\sim t$. In this range, 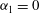 $\unicode[STIX]{x1D6FC}_{1}=0$ and
$\unicode[STIX]{x1D6FC}_{1}=0$ and 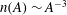 $n(A)\sim A^{-3}$. At intermediate scales (
$n(A)\sim A^{-3}$. At intermediate scales (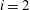 $i=2$) sufficiently far from the forcing and the largest vortex, there is a range with a scale-invariant vortex size distribution. We predict that in this range the vortex enstrophy
$i=2$) sufficiently far from the forcing and the largest vortex, there is a range with a scale-invariant vortex size distribution. We predict that in this range the vortex enstrophy 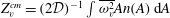 $Z_{v}^{cm}=(2{\mathcal{D}})^{-1}\int \overline{\unicode[STIX]{x1D714}_{v}^{2}}An(A)\,\text{d}A$ is conserved and
$Z_{v}^{cm}=(2{\mathcal{D}})^{-1}\int \overline{\unicode[STIX]{x1D714}_{v}^{2}}An(A)\,\text{d}A$ is conserved and 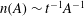 $n(A)\sim t^{-1}A^{-1}$. The final range (
$n(A)\sim t^{-1}A^{-1}$. The final range (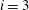 $i=3$), which extends over the largest vortex-containing scales, conserves
$i=3$), which extends over the largest vortex-containing scales, conserves 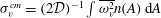 $\unicode[STIX]{x1D70E}_{v}^{cm}=(2{\mathcal{D}})^{-1}\int \overline{\unicode[STIX]{x1D714}_{v}^{2}}n(A)\,\text{d}A$. If
$\unicode[STIX]{x1D70E}_{v}^{cm}=(2{\mathcal{D}})^{-1}\int \overline{\unicode[STIX]{x1D714}_{v}^{2}}n(A)\,\text{d}A$. If 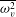 $\overline{\unicode[STIX]{x1D714}_{v}^{2}}$ is constant in time, this is equivalent to conservation of vortex number
$\overline{\unicode[STIX]{x1D714}_{v}^{2}}$ is constant in time, this is equivalent to conservation of vortex number 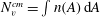 $N_{v}^{cm}=\int n(A)\,\text{d}A$. This regime represents a ‘front’ of sparse vortices, which are effectively point-like; in this range we predict
$N_{v}^{cm}=\int n(A)\,\text{d}A$. This regime represents a ‘front’ of sparse vortices, which are effectively point-like; in this range we predict 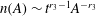 $n(A)\sim t^{r_{3}-1}A^{-r_{3}}$. Allowing for time-varying
$n(A)\sim t^{r_{3}-1}A^{-r_{3}}$. Allowing for time-varying 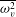 $\overline{\unicode[STIX]{x1D714}_{v}^{2}}$ results in a small but significant correction to these temporal dependences. High-resolution numerical simulations verify the predicted vortex and spectral peak growth rates, as well as the theoretical picture of the three scaling ranges in the vortex population. Vortices steepen the energy spectrum
$\overline{\unicode[STIX]{x1D714}_{v}^{2}}$ results in a small but significant correction to these temporal dependences. High-resolution numerical simulations verify the predicted vortex and spectral peak growth rates, as well as the theoretical picture of the three scaling ranges in the vortex population. Vortices steepen the energy spectrum 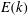 $E(k)$ past the classical
$E(k)$ past the classical 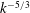 $k^{-5/3}$ scaling in the range
$k^{-5/3}$ scaling in the range 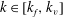 $k\in [k_{f},k_{v}]$, where
$k\in [k_{f},k_{v}]$, where 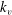 $k_{v}$ is the wavenumber associated with the largest vortex, while at larger scales the slope approaches
$k_{v}$ is the wavenumber associated with the largest vortex, while at larger scales the slope approaches 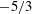 $-5/3$. Though vortices disrupt the classical scaling, their number density distribution and evolution reveal deeper and more complex scale invariance, and suggest an effective theory of the inverse cascade in terms of vortex interactions.
$-5/3$. Though vortices disrupt the classical scaling, their number density distribution and evolution reveal deeper and more complex scale invariance, and suggest an effective theory of the inverse cascade in terms of vortex interactions.