Article contents
Scaling regimes in spherical shell rotating convection
Published online by Cambridge University Press: 04 November 2016
Abstract
Rayleigh–Bénard convection in rotating spherical shells can be considered as a simplified analogue of many astrophysical and geophysical fluid flows. Here, we use three-dimensional direct numerical simulations to study this physical process. We construct a dataset of more than 200 numerical models that cover a broad parameter range with Ekman numbers spanning 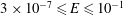 $3\times 10^{-7}\leqslant E\leqslant 10^{-1}$, Rayleigh numbers within the range
$3\times 10^{-7}\leqslant E\leqslant 10^{-1}$, Rayleigh numbers within the range 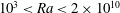 $10^{3}<Ra<2\times 10^{10}$ and a Prandtl number of unity. The radius ratio
$10^{3}<Ra<2\times 10^{10}$ and a Prandtl number of unity. The radius ratio 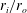 $r_{i}/r_{o}$ is 0.6 in all cases and gravity is assumed to be proportional to
$r_{i}/r_{o}$ is 0.6 in all cases and gravity is assumed to be proportional to 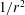 $1/r^{2}$. We investigate the scaling behaviours of both local (length scales, boundary layers) and global (Nusselt and Reynolds numbers) properties across various physical regimes from onset of rotating convection to weakly rotating convection. Close to critical, the convective flow is dominated by a triple force balance between viscosity, Coriolis force and buoyancy. For larger supercriticalities, a small subset of our numerical data approach the asymptotic diffusivity-free scaling of rotating convection
$1/r^{2}$. We investigate the scaling behaviours of both local (length scales, boundary layers) and global (Nusselt and Reynolds numbers) properties across various physical regimes from onset of rotating convection to weakly rotating convection. Close to critical, the convective flow is dominated by a triple force balance between viscosity, Coriolis force and buoyancy. For larger supercriticalities, a small subset of our numerical data approach the asymptotic diffusivity-free scaling of rotating convection 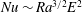 $Nu\sim Ra^{3/2}E^{2}$ in a narrow fraction of the parameter space delimited by
$Nu\sim Ra^{3/2}E^{2}$ in a narrow fraction of the parameter space delimited by 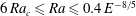 $6\,Ra_{c}\leqslant Ra\leqslant 0.4\,E^{-8/5}$. Using a decomposition of the viscous dissipation rate into bulk and boundary layer contributions, we establish a theoretical scaling of the flow velocity that accurately describes the numerical data. In rapidly rotating turbulent convection, the fluid bulk is controlled by a triple force balance between Coriolis, inertia and buoyancy, while the remaining fraction of the dissipation can be attributed to the viscous friction in the Ekman layers. Beyond
$6\,Ra_{c}\leqslant Ra\leqslant 0.4\,E^{-8/5}$. Using a decomposition of the viscous dissipation rate into bulk and boundary layer contributions, we establish a theoretical scaling of the flow velocity that accurately describes the numerical data. In rapidly rotating turbulent convection, the fluid bulk is controlled by a triple force balance between Coriolis, inertia and buoyancy, while the remaining fraction of the dissipation can be attributed to the viscous friction in the Ekman layers. Beyond 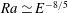 $Ra\simeq E^{-8/5}$, the rotational constraint on the convective flow is gradually lost and the flow properties continuously vary to match the regime changes between rotation-dominated and non-rotating convection. We show that the quantity
$Ra\simeq E^{-8/5}$, the rotational constraint on the convective flow is gradually lost and the flow properties continuously vary to match the regime changes between rotation-dominated and non-rotating convection. We show that the quantity 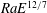 $RaE^{12/7}$ provides an accurate transition parameter to separate rotating and non-rotating convection.
$RaE^{12/7}$ provides an accurate transition parameter to separate rotating and non-rotating convection.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 115
- Cited by



