Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Short, Mark
Quirk, James J.
Meyer, Chad D.
and
Chiquete, Carlos
2016.
Steady detonation propagation in a circular arc: a Detonation Shock Dynamics model.
Journal of Fluid Mechanics,
Vol. 807,
Issue. ,
p.
87.
Wilkinson, S. D.
Braithwaite, M.
Nikiforakis, N.
and
Michael, L.
2017.
A complete equation of state for non-ideal condensed phase explosives.
Journal of Applied Physics,
Vol. 122,
Issue. 22,
Romick, Christopher M.
and
Aslam, Tariq D.
2017.
High-order shock-fitted detonation propagation in high explosives.
Journal of Computational Physics,
Vol. 332,
Issue. ,
p.
210.
Anderson, E. K.
Short, M.
and
Jackson, S. I.
2017.
Cylinder test wall velocity profiles and product energy for an ammonium nitrate and aluminum explosive.
Vol. 1793,
Issue. ,
p.
030018.
Whitworth, N. J.
and
Childs, M.
2017.
Determination of detonation wave boundary angles via hydrocode simulations using CREST.
Vol. 1793,
Issue. ,
p.
040028.
Tappan, Alexander S.
Wixom, Ryan R.
and
Knepper, Robert
2017.
Geometry effects on detonation in vapor-deposited hexanitroazobenzene (HNAB).
Vol. 1793,
Issue. ,
p.
030036.
Jackson, Scott I.
2017.
The dependence of Ammonium-Nitrate Fuel-Oil (ANFO) detonation on confinement.
Proceedings of the Combustion Institute,
Vol. 36,
Issue. 2,
p.
2791.
Rodriguez, George
and
Gilbertson, Steve
2017.
Ultrafast Fiber Bragg Grating Interrogation for Sensing in Detonation and Shock Wave Experiments.
Sensors,
Vol. 17,
Issue. 2,
p.
248.
Li, Kebin
Li, Xiaojie
Yan, Honghao
Wang, Xiaohong
and
Miao, Yusong
2018.
New approaches for evaluating detonation properties of commercial explosives using a novel continuous velocity probe.
Measurement Science and Technology,
Vol. 29,
Issue. 11,
p.
115901.
Chiquete, Carlos
Short, Mark
Meyer, Chad D.
and
Quirk, James J.
2018.
Calibration of the Pseudo-Reaction-Zone model for detonation wave propagation.
Combustion Theory and Modelling,
Vol. 22,
Issue. 4,
p.
744.
Jiao, Qingjie
Song, Haitong
Nie, Jianxin
Liu, Rongqiang
Xu, Xinchun
and
Wen, Yuquan
2018.
Diameter Effect on the Propagation of Curved Detonation Waves in Micro‐Channel Charges Within a Strong Confinement.
Propellants, Explosives, Pyrotechnics,
Vol. 43,
Issue. 8,
p.
771.
Higgins, Andrew
Loiseau, Jason
and
Mi, Xiao Cheng
2018.
Detonation velocity/diameter relation in gelled explosive with inert inclusions.
Vol. 1979,
Issue. ,
p.
100019.
Handley, C. A.
Lambourn, B. D.
Whitworth, N. J.
James, H. R.
and
Belfield, W. J.
2018.
Understanding the shock and detonation response of high explosives at the continuum and meso scales.
Applied Physics Reviews,
Vol. 5,
Issue. 1,
Short, Mark
Quirk, James J.
Chiquete, Carlos
and
Meyer, Chad D.
2018.
Detonation propagation in a circular arc: reactive burn modelling.
Journal of Fluid Mechanics,
Vol. 835,
Issue. ,
p.
970.
Jackson, Scott I.
2018.
Scaling of the detonation product state with reactant kinetic energy.
Combustion and Flame,
Vol. 190,
Issue. ,
p.
240.
Short, Mark
and
Quirk, James J.
2018.
The effect of compaction of a porous material confiner on detonation propagation.
Journal of Fluid Mechanics,
Vol. 834,
Issue. ,
p.
434.
Chiquete, Carlos
and
Short, Mark
2019.
Characteristic path analysis of confinement influence on steady two-dimensional detonation propagation.
Journal of Fluid Mechanics,
Vol. 863,
Issue. ,
p.
789.
Anderson, Eric K.
and
Jackson, Scott I.
2019.
The dependence of Ammonal detonation performance on cylinder test scale.
Combustion and Flame,
Vol. 208,
Issue. ,
p.
369.
O'Grady, Caitlin
Knepper, Robert
Marquez, Michael
and
Tappan, Alexander S.
2019.
Microsandwich Test for Equation of State (EOS) Data of Vapor‐Deposited Hexanitroazobenzene (HNAB).
Propellants, Explosives, Pyrotechnics,
Vol. 44,
Issue. 5,
p.
572.
Jackson, Scott I.
Chiquete, Carlos
and
Short, Mark
2019.
An intrinsic velocity–curvature–acceleration relationship for weakly unstable gaseous detonations.
Proceedings of the Combustion Institute,
Vol. 37,
Issue. 3,
p.
3601.
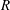 $R$) to slab thickness (
$R$) to slab thickness (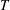 $T$) at each detonation phase velocity (
$T$) at each detonation phase velocity (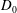 $D_{0}$) is such that
$D_{0}$) is such that 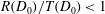 $R(D_{0})/T(D_{0})<1$. The variation in the
$R(D_{0})/T(D_{0})<1$. The variation in the 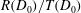 $R(D_{0})/T(D_{0})$ scaling is investigated with two detonation shock dynamics (DSD) models: a lower-order model relates the normal detonation velocity to local shock curvature, while a higher-order model includes the effect of front acceleration and transverse flow. The experimentally observed
$R(D_{0})/T(D_{0})$ scaling is investigated with two detonation shock dynamics (DSD) models: a lower-order model relates the normal detonation velocity to local shock curvature, while a higher-order model includes the effect of front acceleration and transverse flow. The experimentally observed 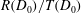 $R(D_{0})/T(D_{0})$ (
$R(D_{0})/T(D_{0})$ (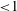 ${<}1$) scaling behaviour for PBX 9501 and PBX 9502 is captured by the lower-order DSD theory, revealing that the variation in the scale factor is due to a difference in the slab and axisymmetric components of the curvature along the shock in the cylindrical geometry. The higher-order DSD theory is required to capture the observed
${<}1$) scaling behaviour for PBX 9501 and PBX 9502 is captured by the lower-order DSD theory, revealing that the variation in the scale factor is due to a difference in the slab and axisymmetric components of the curvature along the shock in the cylindrical geometry. The higher-order DSD theory is required to capture the observed 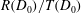 $R(D_{0})/T(D_{0})$ (
$R(D_{0})/T(D_{0})$ (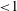 ${<}1$) scaling behaviour for ANFO. An asymptotic analysis of the lower-order DSD formulation describes the geometric scaling of the detonation phase velocity between the cylinder and slab geometries as the detonation phase velocity approaches the Chapman–Jouguet value.
${<}1$) scaling behaviour for ANFO. An asymptotic analysis of the lower-order DSD formulation describes the geometric scaling of the detonation phase velocity between the cylinder and slab geometries as the detonation phase velocity approaches the Chapman–Jouguet value.


