Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T02:21:06.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling laws for the thrust production of flexible pitching panels

Published online by Cambridge University Press:  30 August 2013

Peter A. Dewey ,
Birgitt M. Boschitsch ,
Keith W. Moored ,
Howard A. Stone  and
Alexander J. Smits
Peter A. Dewey*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Birgitt M. Boschitsch
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Keith W. Moored
Affiliation:
Department of Mechanical Engineering and Mechanics, Lehigh University, Bethlehem, PA 18015, USA
Howard A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Alexander J. Smits
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Monash University, Clayton, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

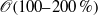We present experimental results on the role of flexibility and aspect ratio in bio-inspired aquatic propulsion. Direct thrust and power measurements are used to determine the propulsive efficiency of flexible panels undergoing a leading-edge pitching motion. We find that flexible panels can give a significant amplification of thrust production of $\mathscr{O}(100{\unicode{x2013}} 200\hspace{0.167em} \% )$ and propulsive efficiency of 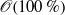$\mathscr{O}(100\hspace{0.167em} \% )$ when compared to rigid panels. The data highlight that the global maximum in propulsive efficiency across a range of panel flexibilities is achieved when two conditions are simultaneously satisfied: (i) the oscillation of the panel yields a Strouhal number in the optimal range (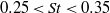$0. 25\lt \mathit{St}\lt 0. 35$) predicted by Triantafyllou, Triantafyllou & Grosenbaugh (J. Fluid Struct., vol. 7, 1993, pp. 205–224); and (ii) this frequency of motion is tuned to the structural resonant frequency of the panel. In addition, new scaling laws for the thrust production and power input to the fluid are derived for the rigid and flexible panels. It is found that the dominant forces are the characteristic elastic force and the characteristic fluid force. In the flexible regime the data scale using the characteristic elastic force and in the rigid limit the data scale using the characteristic fluid force.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Propulsion Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , pp. 29 - 46
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. 2008 Optimal flexibility of a flexible appendage in an inviscid fluid. J. Fluid Mech. 614, 355–380.Google Scholar
Alben, S. 2010 Passive and active bodies in vortex streets. J. Fluid Mech. 642, 95–125.Google Scholar
Alben, S., Witt, C., Baker, T. V., Anderson, E. & Lauder, G. V. 2012 Dynamics of freely swimming flexible foils. Phys. Fluids 24, 051901.Google Scholar
Allen, J. J. & Smits, A. J. 2001 Energy harvesting eel. J. Fluid Struct. 15, 629–640.CrossRefGoogle Scholar
Betz, A. 1912 Ein beitrag zur erklaerung des segelfluges. Z. Flugtech. Motorluftsch. 3, 269–270.Google Scholar
Buchholz, J. H. J., Clark, R. P. & Smits, A. J. 2008 Thrust performance of unsteady propulsors using a novel measurement system, and corresponding wake patterns. Exp. Fluids 45, 461–472.Google Scholar
Buchholz, J. H. J. & Smits, A. J. 2008 The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.CrossRefGoogle ScholarPubMed
Clark, R. P. & Smits, A. J. 2006 Thrust production and wake structure of a batoid-inspired oscillating fin. J. Fluid Mech. 562, 415–429.Google Scholar
Dai, H., Luo, H., de Sousa, P. J. S. A. Ferreira & Doyle, J. F. 2012 Thrust performance of a flexible low-aspect-ratio pitching panel. Phys. Fluids 24, 101903.Google Scholar
Daniel, T. L. & Combes, S. A. 2002 Flexible wings and fins: bending by inertial or fluid-dynamic forces. Integr. Compar. Biol. 42, 1044–1049.Google Scholar
Dewey, P. A., Carriou, A. & Smits, A. J. 2012 On the relationship between efficiency and wake structure of a batoid-inspired oscillating fin. J. Fluid Mech. 691, 245–266.CrossRefGoogle Scholar
Eldredge, J. F., Toomey, J. & Medina, A. 2010 On the roles of chord-wise flexibility in a flapping wing with hovering kinematics. J. Fluid Mech. 659, 94–115.CrossRefGoogle Scholar
Green, M. A. & Smits, A. J. 2008 Effects of three-dimensionality on thrust production by a pitching panel. J. Fluid Mech. 615, 211–220.CrossRefGoogle ScholarPubMed
Heathcote, S., Wang, Z. & Gursul, I. 2008 Effect of spanwise flexibility on flapping wing propulsion. J. Fluid Struct. 24, 183–199.CrossRefGoogle Scholar
Kang, C. K., Aono, H., Cesnik, C. E. S. & Shyy, W. 2011 Effects of flexibility on the aerodynamic performance of flapping wings. J. Fluid Mech. 689, 32–74.CrossRefGoogle Scholar
Katz, J. & Weihs, D. 1978 Hydrodynamic propulsion by large amplitude oscillation of an aerofoil with chordwise flexibility. J. Fluid Mech. 88, 485–497.Google Scholar
Knoller, R. 1909 Die gesetze des luftwiderstandes. Flug Motortech. 3 (21), 1–7.Google Scholar
Lauder, G. V., Madden, P. G. A, Tangorra, J. L., Anderson, E. & Baker, T. V. 2011 Bioinspiration from fish for smart material design and function. Smart Mater. Struct. 20, 1–13.Google Scholar
Leftwich, M. C., Tytell, E. D., Cohen, A. H. & Smits, A. J. 2012 Wake structures behind a swimming robotic lamprey with a passively flexible tail. J. Exp. Biol. 215, 416–425.Google Scholar
Lewin, G. C. & Haj-Hariri, H. 2003 Modelling thrust generation of a two-dimensional heaving aerofoil in a viscous flow. J. Fluid Mech. 492, 339–362.Google Scholar
Masoud, H. & Alexeev, A. 2010 Resonance of flexible flapping wings at low Reynolds number. Phys. Rev. E 81, 1–5.Google Scholar
Michelin, S. & Smith, S. G Llewellyn 2009 Resonance and propulsion performance of a heaving flexible wing. Phys. Fluids 21, 1–15.CrossRefGoogle Scholar
Moored, K. W., Dewey, P. A., Haj-Hariri, H. & Smits, A. J. 2012 Hydrodynamic wake resonance as an underlying principle of efficient unsteady propulsion. J. Fluid Mech. 708, 329–348.CrossRefGoogle Scholar
Moored, K. W., Dewey, P. A., Leftwich, M. C., Bart-Smith, H. & Smits, A. J. 2011 Bioinspired propulsion mechanisms based on manta ray locomotion. Marine Technol. Soc. 45, 110–118.Google Scholar
Ramananarivo, S., Godoy-Diana, R. & Thiria, B. 2011 Rather than resonance, flapping wing flyers may play on aerodynamics to improve performance. Proc. Natl Acad. Sci. 108, 5964–5969.CrossRefGoogle ScholarPubMed
Spagnolie, S. E., Moret, L., Shelley, M. & Zhang, J. 2010 Surprising behaviours in locomotion with passive pitching. Phys. Fluids 22, 1–20.Google Scholar
Sunada, S. 2002 Optical measurements of the deformation motion, and generated force of the wings of a moth, Mythimna Separata (Walker). JSME Intl J. Ser. B 45, 836–842.Google Scholar
Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. 2003 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 435, 707–711.Google Scholar
Theodorsen, T. 1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Report 496.Google Scholar
Thiria, B. & Godoy-Diana, R. 2010 How wing compliance drives the efficiency of self-propelled flapping flyers. Phys. Rev. E 82, 015303(R).Google Scholar
Timoshenko, S. 1974 Vibration Problems in Engineering. John Wiley and Sons.Google Scholar
Triantafyllou, M. S., Techet, A. H. & Hover, F. S. 2004 Review of experimental work in biomimetic foils. IEEE J. Ocean. Engng 29, 585–594.Google Scholar
Triantafyllou, G. S., Triantafyllou, M. S. & Grosenbaugh, M. A. 1993 Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluid Struct. 7, 205–224.Google Scholar
Vanella, M., Fitzgerald, T., Preidikman, S., Balaras, E. & Balachandran, B. 2009 Influence of flexibility on the aerodynamic performance of a hovering wing. J. Exp. Biol. 212, 95–105.CrossRefGoogle ScholarPubMed