Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T18:56:49.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Role of transversal concentration gradient in detonation propagation

Published online by Cambridge University Press:  22 February 2019

Wenhu Han Open the ORCID record for Wenhu Han [Opens in a new window] ,
Cheng Wang  and
Chung K. Law
Wenhu Han*
Affiliation:
State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China
Cheng Wang*
Affiliation:
State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China
Chung K. Law
Affiliation:
Center for Combustion Energy, Tsinghua University, Beijing 100084, China Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

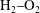The role of a transversal concentration gradient in detonation propagation in a two-dimensional channel filled with an $\text{H}_{2}{-}\text{O}_{2}$ mixture is examined by high-resolution simulation. Results show that, compared to propagation in homogeneous media, a concentration gradient reduces the average detonation velocity because of the delay in reaching downstream reaction equilibrium, leading to a large amount of unreacted 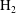$\text{H}_{2}$ and hence significant species fluctuations. The transversal concentration gradient also enhances the cellular detonation instability. Steepening it reduces considerably the number of triple points on the front, lengthens the global detonation front structure on average and consequently increases the deficit of the average detonation velocity. It is further found that the interaction of the leading shock with the transversal concentration gradient influences the formation of local 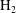$\text{H}_{2}$ bump and thus the unreacted pocket behind the front, while the transverse wave causes mixing and burning of the residue fuel downstream. Nevertheless, for the steepened concentration gradient, a transverse detonation is present and consumes the fuel in the compressed and preheated zone by the leading shock; consequently, the detonation velocity deficit is not increased significantly for detonation with the single-head propagation mode close to the limit.

JFM classification

Compressible Flows: Detonation waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 602 - 649
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auban, O., Zboray, R. & Paladino, D. 2007 Investigation of large-scale gas mixing and stratification phenomena related to LWR containment studies in the PANDA facility. Nucl. Engng Des. 237, 409–419.10.1016/j.nucengdes.2006.07.011Google Scholar
Austin, J. M. 2003 The Role of Instability in Gaseous Detonation. California Institute of Technology.Google Scholar
Austin, J. M., Pintgen, F. & Shepherd, J. E. 2005 Lead shock oscillation and decoupling in propagating detonations. Proc. Combust. Inst. 30, 1849–1857.10.1016/j.proci.2004.08.157Google Scholar
Boeck, L. R., Berger, F. M., Hasslberger, J. & Sattelmayer, T. 2016 Detonation propagation in hydrogen–air mixtures with transverse concentration gradients. Shock Waves 26, 181–192.10.1007/s00193-015-0598-8Google Scholar
Calhoon, W. H. & Sinha, N. 2005 Detonation wave propagation in concentration gradients. In Proc. 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, AIAA-2005-1167. American Institute of Aeronautics and Astronautics.Google Scholar
Edwards, D. H., Jones, A. T. & Phillips, D. E. 1976 The variation in strength of transverse shocks in detonation waves. J. Phys. D: Appl. Phys. 9, 1331–1342.10.1088/0022-3727/9/9/010Google Scholar
Ettner, F., Vollmer, K. G. & Sattelmayer, T. 2010 Numerical investigation of DDT in inhomogeneous hydrogen–air mixtures. In 8th International Symposium on Hazards, Prevention and Mitigation of Industrial Explosions, 5–10 September, Yokohama, Japan.Google Scholar
Ettner, F., Vollmer, K. G. & Sattelmayer, T. 2013 Mach reflection in detonations propagating through a gas with a concentration gradient. Shock Waves 23, 201–206.10.1007/s00193-012-0385-8Google Scholar
Gaathaug, A. V., Vaagsaether, K. & Bjerketvedt, D. 2014 Detonation propagation in a reactive layer: the role of detonation front stability. In Proceedings of the 10th International Symposium on Hazards, Prevention and Mitigation of Industrial Explosions, Bergen, Norway.Google Scholar
Gamezo, V. N., Desbordes, D. & Oran, E. 1999 Formation and evolution of two-dimensional cellular detonations. Combust. Flame 116, 154–165.10.1016/S0010-2180(98)00031-5Google Scholar
Gamezo, V. N., Vasil’v, A. A., Khokhlov, A. M., Oran, E. S. & Parvar, S. 2000 Fine cellular structures produced by marginal detonations. Proc. Combust. Inst. 28, 611–617.10.1016/S0082-0784(00)80261-1Google Scholar
Ishii, K. & Kojima, M. 2007 Behavior of detonation propagation in mixtures with concentration gradients. Shock Waves 17, 95–102.10.1007/s00193-007-0093-yGoogle Scholar
Jiang, G. S. & Shu, C. W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126, 202–228.10.1006/jcph.1996.0130Google Scholar
Ju, Y. G., Guo, H. S., Kaoru, M. & Liu, F. S. 1997 On the extinction limit and flammability limit of non-adiabatic stretched methane–air premixed flames. J. Fluid Mech. 342, 315–334.10.1017/S0022112097005636Google Scholar
Ju, Y. G., Guo, H. S., Liu, F. S. & Kaoru, M. 1999 Effects of the Lewis number and radiative heat loss on the bifurcation and extinction of CH4 /O2 –N2 –He flames. J. Fluid Mech. 379, 165–190.10.1017/S0022112098003231Google Scholar
Kaneshige, M. & Shepherd, J. E.1997 Detonation database. Explosion Dynamics Laboratory Report FM97-8, GALCIT 2009.5.Google Scholar
Kasimov, A. R. & Stewart, D. S. 2004 On the dynamics of self-sustained one-dimensional detonations: a numerical study in the shock-attached frame detonation propagation through a gradient in fuel composition. Phys. Fluids 16, 3566–3578.10.1063/1.1776531Google Scholar
Kennedy, C. A. & Carpenter, M. H. 2003 Additive Runge–Kutta schemes for convection diffusion reaction equations. Appl. Numer. Maths 44, 139–181.10.1016/S0168-9274(02)00138-1Google Scholar
Kessler, D. A., Gamezo, V. N. & Oran, E. S. 2011 Detonation propagation through a gradient in fuel composition. In Proceedings of the 23th International Colloquium on the Dynamics of Explosions and Reacting Systems, Irvine, CA.Google Scholar
Kessler, D. A., Gamezo, V. N. & Oran, E. S. 2012 Gas-phase detonation propagation in mixture composition gradients. Proc. R. Soc. Lond. A 370, 567–596.Google Scholar
Kuznetsov, M. S., Alekseev, V. I., Dorofeev, S. B., Matsukov, I. D. & Boccio, J. L. 1998 Detonation propagation, decay, and reinitiation in nonuniform gaseous mixtures. Proc. Combust. Inst. 27, 2241–2247.10.1016/S0082-0784(98)80073-8Google Scholar
Kuznetsov, M. S., Dorofeev, S. B., Efimenko, A. A., Alekseev, V. I. & Breitung, W. 1997 Experimental and numerical studies on transmission of gaseous detonation to a less sensitive mixture. Shock Waves 7, 297–304.10.1007/s001930050084Google Scholar
Lieberman, D. H., Shepherd, J. E. & Brossard, J. 2007 Detonation interaction with a diffuse interface and subsequent chemical reaction. Shock Waves 16, 421–429.10.1007/s00193-007-0080-3Google Scholar
Mahmoudi, Y., Karimi, N., Deiterding, R. & Emami, S. 2014 Hydrodynamic instabilities in gaseous detonations: comparison of Euler, Navier–Stokes, and large-eddy simulation. J. Propul. Power 30, 384–396.Google Scholar
Mahmoudi, Y. & Mazaheri, K. 2010 High resolution numerical simulation of the structure of 2-D gaseous detonations. Proc. Combust. Inst. 33, 2187–2194.10.1016/j.proci.2010.07.083Google Scholar
Mahmoudi, Y. & Mazaheri, K. 2015 High resolution numerical simulation of triple point collision and origin of unburned gas pockets in turbulent detonations. Acta Astron. 115, 40–51.10.1016/j.actaastro.2015.05.014Google Scholar
Massa, I., Austin, J. M. & Jackson, T. L. 2007 Triple-point shear layers in gaseous detonation waves. J. Fluid Mech. 586, 205–248.10.1017/S0022112007007008Google Scholar
Maxwell, B. M., Bhattacharjee, R. R., Lau-Chapdelaine, S. S. M., Falle, S. A. E. G., Sharpe, G. J. & Radulescu, M. I. 2017 Influence of turbulent fluctuations on detonation propagation. J. Fluid Mech. 818, 646–696.10.1017/jfm.2017.145Google Scholar
Mazaheri, K., Mahmoudi, Y., Sabzpooshani, M. & Radulescu, M. I. 2015 Experimental and numerical investigation of propagation mechanism of gaseous detonations in channels with porous walls. Combust. Flame 162, 2638–2659.10.1016/j.combustflame.2015.03.015Google Scholar
Mi, X. C., Timofeev, E. V. & Higgins, A. J. 2017 Effect of spatial discretization of energy on detonation wave propagation. J. Fluid Mech. 817, 306–338.10.1017/jfm.2017.81Google Scholar
Oran, E. S., Jones, D. A. & Sichel, M. 1992 Numerical simulations of detonation transmission. Proc. R. Soc. Lond. A 436, 267–297.Google Scholar
Oran, E. S., Weber, J. W., Stefaniw, E. I., Lefebvre, M. H. & Anderson, J. D. 1998 A numerical study of a two-dimensional H2 –O2 –Ar detonation using a detailed chemical reaction model. Combust. Flame 113, 147–163.10.1016/S0010-2180(97)00218-6Google Scholar
Oran, E. S., Young, T. R., Boris, J. P., Picone, J. M. & Edwards, D. H. 1982 Numerical simulation of flame acceleration and deflagration-to-detonation transition in hydrogen–air mixtures with concentration gradients. Intl J. Hydrogen Energy 19, 573–582.Google Scholar
Pintgen, F., Eckett, C. A., Austin, J. M. & Shepherd, J. E. 2003 Direct observations of reaction zone structure in propagating detonations. Combust. Flame 133, 211–229.10.1016/S0010-2180(02)00458-3Google Scholar
Radulescu, M. I. 2003 The Propagation and Failure Mechanism of Gaseous Detonations: Experiments in Porous-walled Tubes. McGill University.Google Scholar
Radulescu, M., Sharpe, G., Law, C. K. & Lee, J. H. S. 2007 The hydrodynamic structure of unstable cellular detonations. J. Fluid Mech. 580, 31–81.Google Scholar
Radulescu, M. I., Sharpe, G. J., Lee, J. H. S., Kiyanda, C. B., Higgins, A. J. & Hanson, R. K. 2005 The ignition mechanism in irregular structure gaseous detonations. Proc. Combust. Inst. 30, 1859–1867.10.1016/j.proci.2004.08.047Google Scholar
Romick, C. M., Aslam, T. D. & Powers, J. M. 2015 Verified and validated calculation of unsteady dynamics of viscous hydrogen–air detonations. J. Fluid Mech. 769, 154–181.10.1017/jfm.2015.114Google Scholar
Sabzpooshani, M. & Mazaheri, K. 2009 Formation of unburnt pockets in gaseous detonation. Combust. Explos. Shock Waves 45, 182–189.10.1007/s10573-009-0024-6Google Scholar
Sánchez, A. L. & Williams, F. A. 2014 Recent advances in understanding of flammability characteristics of hydrogen. Prog. Energy Combust. Sci. 41, 1–55.Google Scholar
Sharpe, G. J. 2001 Transverse wave in numerical simulations of cellular detonation. J. Fluid Mech. 447, 31–51.Google Scholar
Sochet, I., Lamy, T. & Brossard, J. 2000 Experimental investigation on the detonability of non-uniform mixtures. Shock Waves 10, 363–367.Google Scholar
Subbotin, V. 1975 Two kinds of transverse wave structures in multi-front detonation. Fiz. Gor. Vzryva 11, 96–102.Google Scholar
Thomas, G. O., Sutton, P. & Edwards, D. H. 1991 The behavior of detonation waves at concentration gradients. Combust. Flame 84, 312–322.Google Scholar
Vollmer, K. G., Ettner, F. & Sattelmayer, T. 2012 Deflagration-to-detonation transition in hydrogen/air mixtures with a concentration gradient. Combust. Sci. Technol. 184, 1903–1915.10.1080/00102202.2012.690652Google Scholar
Wang, C., Shu, C. W., Han, W. H. & Ning, J. G. 2013 High resolution WENO simulation of 3D detonation waves. Combust. Flame 160, 447–462.10.1016/j.combustflame.2012.10.002Google Scholar
Wang, C. J. & Wen, J. X. 2017 Numerical simulation of flame acceleration and deflagration-to-detonation transition in hydrogen–air mixtures with concentration gradients. Intl J. Hydrogen Energy 42, 7657–7663.10.1016/j.ijhydene.2016.06.107Google Scholar
Wang, X. M. & Law, C. K. 2013 An analysis of the explosion limits of hydrogen–oxygen mixtures. J. Chem. Phys. 138, 134305.Google Scholar
Zhang, X. & Shu, C. W. 2012 Positivity-preserving high order finite difference WENO schemes for compressible Euler equations. J. Comput. Phys. 231, 2245–2258.Google Scholar