Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T09:07:42.691Z Has data issue: false hasContentIssue false
  • English
  • Français

Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows

Published online by Cambridge University Press:  26 September 2014

C. Chin ,
J. Philip ,
J. Klewicki ,
A. Ooi  and
I. Marusic
C. Chin
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
J. Philip*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
J. Klewicki
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
A. Ooi
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
I. Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A detailed analysis of the ‘turbulent inertia’ (TI) term (the wall-normal gradient of the Reynolds shear stress, 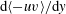$\mathrm{d} \langle -uv\rangle /\mathrm{d} y $), in the axial mean momentum equation is presented for turbulent pipe flows at friction Reynolds numbers 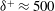$\delta ^{+} \approx 500$, 1000 and 2000 using direct numerical simulation. Two different decompositions for TI are employed to further understand the mean structure of wall turbulence. In the first, the TI term is decomposed into the sum of two velocity–vorticity correlations ($\langle v \omega _z \rangle + \langle - w \omega _y \rangle $) and their co-spectra, which we interpret as an advective transport (vorticity dispersion) contribution and a change-of-scale effect (associated with the mechanism of vorticity stretching and reorientation). In the second decomposition, TI is equivalently represented as the wall-normal gradient of the Reynolds shear stress co-spectra, which serves to clarify the accelerative or decelerative effects associated with turbulent motions at different scales. The results show that the inner-normalised position, 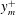$y_m^{+}$, where the TI profile crosses zero, as well as the beginning of the logarithmic region of the wall turbulent flows (where the viscous force is leading order) move outwards in unison with increasing Reynolds number as 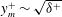$y_m^{+} \sim \sqrt{\delta ^{+}}$ because the eddies located close to 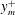$y_m^{+}$ are influenced by large-scale accelerating motions of the type 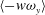$\langle - w \omega _y \rangle $ related to the change-of-scale effect (due to vorticity stretching). These large-scale motions of 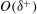$O(\delta ^{+})$ gain a spectrum of larger length scales with increasing $\delta ^{+}$ and are related to the emergence of a secondary peak in the 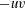$-uv$ co-spectra. With increasing Reynolds number, the influence of the 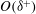$O(\delta ^{+})$ motions promotes viscosity to act over increasingly longer times, thereby increasing the 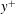$y^{+}$ extent over which the mean viscous force retains leading order. Furthermore, the TI decompositions show that the 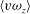$\langle v \omega _z \rangle $ motions (advective transport and/or dispersion of vorticity) are the dominant mechanism in and above the log region, whereas 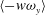$\langle - w \omega _y \rangle $ motions (vorticity stretching and/or reorientation) are most significant below the log region. The motions associated with 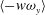$\langle - w \omega _y \rangle $ predominantly underlie accelerations, whereas 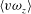$\langle v \omega _z \rangle $ primarily contribute to decelerations. Finally, a description of the structure of wall turbulence deduced from the present analysis and our physical interpretation is presented, and is shown to be consistent with previous flow visualisation studies.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 747 - 769
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Matsuo, Y. 2001 Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. Trans. ASME: J. Fluids Engng 123, 382–393.Google Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
Adrian, R. J. & Marusic, I. 2012 Coherent structures in flow over hydraulic engineering surfaces. J. Hydraul Res. 50, 451–464.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ing.-Arch. 52, 355–377.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15, L41–L44.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google ScholarPubMed
Bernard, P. S. & Handler, R. A. 1990 Reynolds stress and the physics of turbulent momentum transport. J. Fluid Mech. 220, 99–124.CrossRefGoogle Scholar
Buschmann, M. H., Indinger, T. & Gad-el-Hak, M. 2009 Near-wall behavior of turbulent wall-bounded flows. Intl J. Heat Fluid Flow 30, 993–1006.CrossRefGoogle Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.CrossRefGoogle Scholar
Chin, C., Monty, J. P. & Ooi, A. 2014 Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.CrossRefGoogle Scholar
Chin, C., Ooi, A., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from DNS data. Phys. Fluids 22, 115107.CrossRefGoogle Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
Elsinga, G. E., Poelma, C., Schroder, A., Geisler, R., Scarano, F. & Westerweel, J. 2012 Tracking of vortices in a turbulent boundary layer. J. Fluid Mech. 697, 143–188.CrossRefGoogle Scholar
Eyink, G. L. 2008 Turbulent flow in pipes and channels as cross-stream inverse cascades of vorticity. Phys. Fluids 20, 125101.CrossRefGoogle Scholar
Fife, P., Klewicki, J. & Wei, T. 2009 Time averaging in turbulence settings may reveal an infinite hierarchy of length scales. J. Discrete Continuous Dyn. Syst. 24, 781–807.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Klewicki, J. C. 1989 Velocity–vorticity correlations related to the gradients of the Reynolds stresses in parallel turbulent wall flows. Phys. Fluids A 1, 1285–1288.CrossRefGoogle Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME: J. Fluids Engng 9, 094001.Google Scholar
Klewicki, J. 2013a A description of turbulent wall-flow vorticity consistent with mean dynamics. J. Fluid Mech. 737, 176–204.CrossRefGoogle Scholar
Klewicki, J. 2013b Self-similar mean dynamics in turbulent wall-flows. J. Fluid Mech. 718, 596–621.CrossRefGoogle Scholar
Klewicki, J., Chin, C., Blackburn, H. M., Ooi, A. & Marusic, I. 2012 Emergence of the four layer dynamical regime in turbulent pipe flow. Phys. Fluids 24 (4), 045107.CrossRefGoogle Scholar
Klewicki, J. C. & Falco, R. E. 1996 Spanwise vorticity structure in turbulent boundary layers. Intl J. Heat Fluid Flow 17, 363–376.CrossRefGoogle Scholar
Klewicki, J., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. Lond. A 365, 823–839.Google ScholarPubMed
Klewicki, J. & Hirschi, C. R. 2004 Flow field properties local to near-wall shear layers in a low Reynolds number turbulent boundary layer. Phys. Fluids 16, 4163–4176.CrossRefGoogle Scholar
Klewicki, J., Murray, J. A. & Falco, R. E. 1995 Vortical motion contributions to stress transport in turbulent boundary layers. Phys. Fluids 6, 277–286.CrossRefGoogle Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstandler, P. W. 1967 The structure of turbulent boundary layer. J. Fluid Mech. 30, 741–773.CrossRefGoogle Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25, 045103.CrossRefGoogle Scholar
Long, R. R. & Chen, T. C. 1981 Experimental evidence for the existence of the mesolayer in turbulent systems. J. Fluid Mech. 105, 19–59.CrossRefGoogle Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (3), 735–743.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. Science 329, 193–196.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009 Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21, 111703.CrossRefGoogle Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694.CrossRefGoogle Scholar
Metzger, M., Lyons, A. & Fife, P. 2008 Mean momentum balance in moderately favourable pressure gradient turbulent boundary layers. J. Fluid Mech. 617, 107–140.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.CrossRefGoogle Scholar
Morrill-Winter, C. & Klewicki, J. 2013 Influences of boundary layer scale separation on the vorticity transport contribution to turbulent inertia. Phys. Fluids 24, 015108.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A. E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to $\delta ^{+}=2000$ . Phys. Fluids 25, 105102.CrossRefGoogle Scholar
Sreenivasan, K. R. 1989 The turbulent boundary layer. In Frontiers in Experimental Fluid Mechanics, pp. 159–209. Springer.CrossRefGoogle Scholar
Sreenivasan, K. R. & Sahay, A. 1997 The persistence of viscous effects in the overlap region, and the mean velocity in turbulent pipe and channel flows. Adv. Fluid Mech. 15, 253–272.Google Scholar
Taylor, G. I. 1932 The transport of vorticity and heat through fluids in turbulent motion. Proc. R. Soc. Lond. A 135, 685–702.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. (vol. 2) , Cambridge University Press.Google Scholar
Townsend, A. A. 1987 Organized eddy structures in turbulent flows. Physico-Chem. Hydrodyn. 8, 23–30.Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54, 1629.CrossRefGoogle Scholar
Wallace, J. M. 1982 On the structure of bounded turbulent shear flow: a personal view. In Developments in Theoretical and Applied Mechanics (ed. Chung, T. J. & Karr, G. R.), vol. XI, pp. 509–521. University of Alabama, Huntsville.Google Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Wei, T. & Willmarth, W. W. 1989 Reynolds number effects on the structures of a turbulent channel flow. J. Fluid Mech. 204, 57–95.CrossRefGoogle Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a $30R$ long turbulent pipe flow at $R^{+}=685$ : large- and very large-scale motions. J. Fluid Mech. 698, 235–281.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar