Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T02:19:39.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Reynolds and dispersive shear stress contributions above highly skewed roughness

Published online by Cambridge University Press:  14 August 2018

Thomas O. Jelly Open the ORCID record for Thomas O. Jelly [Opens in a new window]  and
Angela Busse Open the ORCID record for Angela Busse [Opens in a new window]
Thomas O. Jelly*
Affiliation:
School of Engineering, University of Glasgow, Glasgow G12 8QQ, UK
Angela Busse
Affiliation:
School of Engineering, University of Glasgow, Glasgow G12 8QQ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The roughness functions induced by irregular peak- and/or pit-dominated surfaces in a fully developed turbulent channel flow are studied by direct numerical simulation. A surface generation algorithm is used to synthesise an irregular Gaussian height map with periodic boundaries. 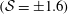The Gaussian height map is decomposed into ‘pits-only’ and ‘peaks-only’ components, which produces two additional surfaces with similar statistical properties, with the exception of skewness, which are equal and opposite $({\mathcal{S}}=\pm 1.6)$. While the peaks-only surface yields a roughness function comparable to that of the Gaussian surface, the pits-only surface exhibits a far weaker roughness effect. Analysis of results is aided by deriving an equation for the roughness function that quantitatively identifies the mechanisms of momentum loss and/or gain. The statistical contributions of ‘form-induced’ and stochastic fluid motions to the roughness function are examined in further detail using quadrant analyses. Above the Gaussian and peaks-only surfaces, the contributions of dispersive and Reynolds shear stresses show a compensating effect, whereas above the pits-only surface, an additive effect is observed. Overall, the results emphasise the sensitivity of the near-wall flow with respect to higher-order topographical parameters, which can, in turn, induce significant differences in the roughness function above a peak- and/or pit-dominated surface.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 852 , 10 October 2018 , pp. 710 - 724
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bons, J. P., Taylor, R. P., McClain, S. T. & Rivir, R. B. 2001 The many faces of turbine surface roughness. J. Turbomach. 123 (4), 739–748.Google Scholar
Busse, A., Lützner, M. & Sandham, N. D. 2015 Direct numerical simulation of turbulent flow over a rough surface based on a surface scan. Comput. Fluids 116, 129–147.Google Scholar
Busse, A., Thakkar, M. & Sandham, N. D. 2017 Reynolds-number dependence of the near-wall flow over irregular rough surfaces. J. Fluid Mech. 810, 196–224.Google Scholar
Chan, L., MacDonald, M., Chung, D., Hutchins, N. & Ooi, A. 2017 Analysis of the coherent and turbulent stresses of a numerically simulated rough wall pipe. J. Phys. Conf. Ser. 822, 012011.Google Scholar
De Marchis, M. & Napoli, E. 2012 Effects of irregular two-dimensional and three-dimensional surface roughness in turbulent channel flows. Intl J. Heat Fluid Flow 36, 7–17.Google Scholar
De Marchis, M., Napoli, E. & Armenio, V. 2010 Turbulence structures over irregular rough surfaces. J. Turbul. 11 (3), 1–32.Google Scholar
Durbin, P. A., Medic, G., Seo, J. M., Eaton, J. K. & Song, S. 2001 Rough wall modification of two-layer k–𝜀. J. Fluids Engng 123 (1), 16–21.Google Scholar
Flack, K. A. & Schultz, M. P. 2010 Review of hydraulic roughness scales in the fully rough regime. J. Fluids Engng 132 (4), 041203.Google Scholar
Flack, K. A. & Schultz, M. P. 2014 Roughness effects on wall-bounded turbulent flows. Phys. Fluids 26 (10), 101305.Google Scholar
Flack, K. A., Schultz, M. P., Barros, J. M. & Kim, Y. C. 2016 Skin-friction behavior in the transitionally-rough regime. Intl J. Heat Fluid Flow 61, 21–30.Google Scholar
Forooghi, P., Stroh, A., Magagnato, F., Jakirlic, S. & Frohnapfel, B. 2017 Towards a universal roughness correlation. ASME J. Fluids Engng 139 (12), 121201.Google Scholar
García-Mayoral, R. & Jiménez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.Google Scholar
Hama, F. R. 1954 Boundary layer characteristics for smooth and rough surfaces. Trans. Soc. Nav. Archit. Mar. Engrs 62, 333–358.Google Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Leonardi, S., Orlandi, P. & Antonia, R. A. 2007 Properties of d-and k-type roughness in a turbulent channel flow. Phys. Fluids 19 (12), 125101.Google Scholar
MacDonald, M., Chan, L., Chung, D., Hutchins, N. & Ooi, A. 2016 Turbulent flow over transitionally rough surfaces with varying roughness densities. J. Fluid Mech. 804, 130–161.Google Scholar
MacDonald, M., Chung, D., Hutchins, N., Chan, L., Ooi, A. & García-Mayoral, R. 2017 The minimal-span channel for rough-wall turbulent flows. J. Fluid Mech. 816, 5–42.Google Scholar
Manes, C., Pokrajac, D., Coceal, O. & McEwan, I. 2008 On the significance of form-induced stress in rough wall turbulent boundary layers. Acta Geophys. 56 (3), 845–861.Google Scholar
Monty, J. P., Dogan, E., Hanson, R., Scardino, A. J., Ganapathisubramani, B. & Hutchins, N. 2016 An assessment of the ship drag penalty arising from light calcareous tubeworm fouling. Biofouling 32 (4), 451–464.Google Scholar
Napoli, E., Armenio, V. & De Marchis, M. 2008 The effect of the slope of irregularly distributed roughness elements on turbulent wall-bounded flows. J. Fluid Mech. 613, 385–394.Google Scholar
Nikora, V., McEwan, I., McLean, S., Coleman, S., Pokrajac, D. & Walters, R. 2007 Double-averaging concept for rough-bed open-channel and overland flows: theoretical background. J. Hydraul. Engng 133 (8), 873–883.Google Scholar
Patir, N. 1978 A numerical procedure for random generation of rough surfaces. Wear 47 (2), 263–277.Google Scholar
Perry, A. E., Schofield, W. H. & Joubert, P. N. 1969 Rough wall turbulent boundary layers. J. Fluid Mech. 37 (2), 383–413.Google Scholar
Pokrajac, D., Campbell, L. J., Nikora, V., Manes, C. & McEwan, I. 2007 Quadrant analysis of persistent spatial velocity perturbations over square-bar roughness. Exp. Fluids 42 (3), 413–423.Google Scholar
Raupach, M. R. & Shaw, R. H. 1982 Averaging procedures for flow within vegetation canopies. Boundary-Layer Meteorol. 22 (1), 79–90.Google Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21 (1), 015104.Google Scholar
Thakkar, M., Busse, A. & Sandham, N. D. 2016 Surface correlations of hydrodynamic drag for transitionally rough engineering surfaces. J. Turbul. 18 (2), 138–169.Google Scholar
Thakkar, M., Busse, A. & Sandham, N. D. 2018 Direct numerical simulation of turbulent channel flow over a surrogate for Nikuradse-type roughness. J. Fluid Mech. 837, R1.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.Google Scholar