Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T02:33:03.558Z Has data issue: false hasContentIssue false
  • English
  • Français

Release of a viscous power-law fluid over an inviscid ocean

Published online by Cambridge University Press:  17 April 2012

Samuel S. Pegler ,
John R. Lister  and
M. Grae Worster
Samuel S. Pegler*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, CMS, Wilberforce Road, Cambridge CB3 0WA, UK
John R. Lister
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, CMS, Wilberforce Road, Cambridge CB3 0WA, UK
M. Grae Worster
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, CMS, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the two- and three-dimensional spreading of a finite volume of viscous power-law fluid released over a denser inviscid fluid and subject to gravitational and capillary forces. In the case of gravity-driven spreading, with a power-law fluid having strain rate proportional to stress to the power , there are similarity solutions with the extent of the current being proportional to 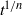in the two-dimensional case and 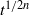in the three-dimensional case. Perturbations from these asymptotic states are shown to retain their initial shape but to decay relatively as 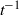in the two-dimensional case and 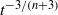in the three-dimensional case. The former is independent of , whereas the latter gives a slower rate of relative decay for fluids that are more shear-thinning. In cases where the layer is subject to a constraining surface tension, we determine the evolution of the layer towards a static state of uniform thickness in which the gravitational and capillary forces balance. The asymptotic form of this convergence is shown to depend strongly on , with rapid finite-time algebraic decay in shear-thickening cases, large-time exponential decay in the Newtonian case and slow large-time algebraic decay in shear-thinning cases.

JFM classification

Geophysical and Geological Flows: Gravity currents Non-Newtonian Flows: Non-Newtonian Flows Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 700 , 10 June 2012 , pp. 63 - 76
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. DiPietro, N. D. & Cox, R. G. 1979 The spreading of a very viscous liquid on a quiescent water surface. Q. J. Mech. Appl. Maths 32, 355–381.Google Scholar
2. Dorsey, C. W. & Manga, M. 1998 The low-Reynolds number spreading of axisymmetric drops and gravity currents along a free surface. Phys. Fluids 10, 3011–3013.CrossRefGoogle Scholar
3. Foda, M. & Cox, R. G. 1980 The spreading of liquid films on a water–air interface. J. Fluid Mech. 101, 33–51.CrossRefGoogle Scholar
4. Hoult, D. P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4, 341–368.CrossRefGoogle Scholar
5. Howell, P. D. 1994 Extensional thin layer flows. PhD thesis, University of Oxford.Google Scholar
6. Koch, D. M. & Koch, D. L. 1995 Numerical and theoretical solutions for a drop spreading below a free fluid surface. J. Fluid Mech. 287, 251–278.CrossRefGoogle Scholar
7. Leppinen, D. & Lister, J. R. 2003 Capillary pinch-off in inviscid fluids. Phys. Fluids 15 (2), 568–578.CrossRefGoogle Scholar
8. Lister, J. R. & Kerr, R. C. 1989 The propagation of two-dimensional and axisymmetric viscous gravity currents at a fluid interface. J. Fluid Mech. 203, 215–249.CrossRefGoogle Scholar
9. Paterson, W. S. B. 1994 The Physics of Glaciers, 3rd edn. Pergamon.Google Scholar
10. Pegler, S. S. & Worster, M. G. 2012 Dynamics of a viscous layer flowing radially over an inviscid ocean. J. Fluid Mech. 696, 152–174.CrossRefGoogle Scholar
11. Robison, R. A. V., Huppert, H. E. & Worster, M. G. 2010 Dynamics of viscous grounding lines. J. Fluid Mech. 648, 363–380.CrossRefGoogle Scholar
12. Sebilleau, J., Lebon, L., Limat, L., Quartier, L. & Receveur, M. 2010 The dynamics and shapes of a viscous sheet spreading on a moving liquid bath. Europhys. Lett. 92, 14003.CrossRefGoogle Scholar