Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T11:10:36.931Z Has data issue: false hasContentIssue false
  • English
  • Français

Relationship between the energy dissipation function and the skin friction law in a turbulent channel flow

Published online by Cambridge University Press:  31 May 2016

Hiroyuki Abe  and
Robert Anthony Antonia
Hiroyuki Abe*
Affiliation:
Japan Aerospace Exploration Agency, Tokyo 182-8522, Japan
Robert Anthony Antonia
Affiliation:
Discipline of Mechanical Engineering, University of Newcastle, NSW 2308, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Integrals of the mean and turbulent energy dissipation rates are examined using direct numerical simulation (DNS) databases in a turbulent channel flow. Four values of the Kármán number (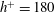$h^{+}=180$, 395, 640 and 1020; 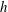$h$ is the channel half-width) are used. Particular attention is given to the functional 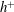$h^{+}$ dependence by comparing existing DNS and experimental data up to 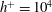$h^{+}=10^{4}$. The logarithmic 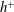$h^{+}$ dependence of the integrated turbulent energy dissipation rate is established for 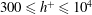$300\leqslant h^{+}\leqslant 10^{4}$, and is intimately linked to the logarithmic skin friction law, viz.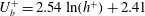$U_{b}^{+}=2.54\ln (h^{+})+2.41$ (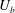$U_{b}$ is the bulk mean velocity). This latter relationship is established on the basis of energy balances for both the mean and turbulent kinetic energy. When 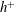$h^{+}$ is smaller than 300, viscosity affects the integrals of both the mean and turbulent energy dissipation rates significantly due to the lack of distinct separation between inner and outer regions. The logarithmic 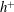$h^{+}$ dependence of 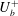$U_{b}^{+}$ is clarified through the scaling behaviour of the turbulent energy dissipation rate $\overline{{\it\varepsilon}}$ in different parts of the flow. The overlap between inner and outer regions is readily established in the region 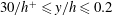$30/h^{+}\leqslant y/h\leqslant 0.2$ for 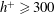$h^{+}\geqslant 300$. 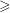At large $h^{+}$ (${\geqslant}$5000) when the finite Reynolds number effect disappears, the magnitude of 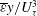$\overline{{\it\varepsilon}}y/U_{{\it\tau}}^{3}$ approaches 2.54 near the lower bound of the overlap region. This value is identical between the channel, pipe and boundary layer as a result of similarity in the constant stress region. As $h^{+}$ becomes large, the overlap region tends to contribute exclusively to the 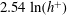$2.54\ln (h^{+})$ dependence of the integrated turbulent energy dissipation rate. The present logarithmic 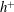$h^{+}$ dependence of 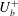$U_{b}^{+}$ is essentially linked to the overlap region, even at small 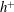$h^{+}$.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 140 - 164
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.CrossRefGoogle Scholar
Abe, H. & Antonia, R. A. 2011 Scaling of normalized mean energy and scalar dissipation rates in a turbulent channel flow. Phys. Fluids 23, 055104.CrossRefGoogle Scholar
Abe, H., Kawamura, H. & Matsuo, Y. 2001 Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. Trans. ASME J. Fluids Engng 123, 382–393.CrossRefGoogle Scholar
Abe, H., Kawamura, H. & Matsuo, Y. 2004a Surface heat-flux fluctuations in a turbulent channel flow up to Re 𝜏 = 1020 with Pr = 0. 025 and 0.71. Intl J. Heat Fluid Flow 25, 404–419.CrossRefGoogle Scholar
Abe, H., Kawamura, H. & Choi, H. 2004b Very large-scale structures and their effects on the wall shear-stress fluctuations in a turbulent channel flow up to Re 𝜏 = 640. Trans. ASME J. Fluids Engng 126, 835–843.CrossRefGoogle Scholar
Abe, H., Kawamura, H., Toh, S. & Itano, T. 2007 Effects of the streamwise computational domain size on DNS of a turbulent channel flow at high Reynolds number. In Advances in Turbulence XI, Proceedings of the 11th EUROMECH European Turbulence Conference, Porto, Portugal, June 25–28, 2007 (ed. Palma, J. M. L. M. & Lopes, A. S.), pp. 233–235. Springer.CrossRefGoogle Scholar
Ahn, J., Lee, J. H., Jang, S. J. & Sung, H. J. 2013 Direct numerical simulations of fully developed turbulent pipe flows for Re 𝜏 = 180, 544 and 934. Intl J. Heat Fluid Flow 44, 222–228.CrossRefGoogle Scholar
Ahn, J., Lee, J. H., Lee, J. L., Kang, J.-H. & Sung, H. J. 2015 Direct numerical simulation of a 30R long turbulent pipe flow at Re 𝜏 = 3008. Phys. Fluids 27, 065110.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Antonia, R. A., Abe, H. & Kawamura, H. 2009 Analogy between velocity and scalar fields in a turbulent channel flow. J. Fluid Mech. 628, 241–268.CrossRefGoogle Scholar
Antonia, R. A., Kim, J. & Browne, L. W. B. 1991 Some characteristics of small-scale turbulence in a turbulent duct flow. J. Fluid Mech. 233, 369–388.CrossRefGoogle Scholar
Antonia, R. A., Teitel, M., Kim, J. & Browne, L. W. B. 1992 Low-Reynolds-number effects in a fully developed turbulent channel flow. J. Fluid Mech. 236, 579–605.CrossRefGoogle Scholar
Afzal, N. 1976 Millikan’s argument at moderately large Reynolds number. Phys. Fluids 19, 600–602.CrossRefGoogle Scholar
Bakken, O. M., Krogstad, P., Ashrafian, A. & Andersson, H. I. 2005 Reynolds number effects in the outer layer of the turbulent flow in a channel with rough walls. Phys. Fluids 17, 065101.CrossRefGoogle Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google ScholarPubMed
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.CrossRefGoogle Scholar
Bradshaw, B. 1967 ‘Inactive’ motion and pressure fluctuations in turbulent boundary layers. J. Fluid Mech. 30, 241–258.CrossRefGoogle Scholar
Chin, C., Monty, J. P. & Ooi, A. 2014 Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.CrossRefGoogle Scholar
Comte-Bellot, G.1963 Contribution à l’étude de la turbulence de conduite. PhD thesis, University of Grenoble (trans. P. Bradshaw ARC 31 609 FM 4102, 1969).Google Scholar
Dean, R. B. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Trans. ASME J. Fluids Engng 100, 215–223.CrossRefGoogle Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
Durst, F., Fischer, M., Jovanović, J. & Kimura, H. 1998 Methods to set up and investigate low Reynolds number, fully developed turbulent plane channel flows. Trans. ASME J. Fluids Engng 120, 496–503.CrossRefGoogle Scholar
Eggels, J. G. M., Unger, F., Weiss, M. R., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–209.CrossRefGoogle Scholar
El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91, 475–495.CrossRefGoogle Scholar
Fischer, M., Jovanović, J. & Durst, F. 2001 Reynolds number effects in the near-wall region of turbulent channel flows. Phys. Fluids 13, 1755–1767.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.CrossRefGoogle Scholar
Furuichi, N., Terao, Y., Wada, Y. & Tsuji, Y. 2015 Friction factor and mean velocity profile for pipe flow at high Reynolds number. Phys. Fluids 27, 095108.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20, 101511.CrossRefGoogle Scholar
Hu, Z. W., Morfey, C. L. & Sandham, N. D. 2006 Wall pressure and shear stress spectra from direct numerical simulations of channel flow. AIAA J. 44 (7), 1541–1549.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.CrossRefGoogle Scholar
Hussain, A. K. M. F. & Reynolds, W. C. 1975 Measurements in fully developed turbulent channel flow. Trans. ASME J. Fluids Engng 97, 568–580.CrossRefGoogle Scholar
Iwamoto, K., Suzuki, Y. & Kasagi, N. 2002 Reynolds number effect on wall turbulence: toward effective feedback control. Intl J. Heat Fluid Flow 23, 678–689.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jiménez, J. & Moser, R. D. 2007 What are we learning from simulating wall turbulence? Phil. Trans. R. Soc. Lond. A 365, 715–732.Google ScholarPubMed
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Klebanoff, P. S.1954 Characteristics of turbulence in a boundary layer with zero pressure gradient. NACA Tech. Rep. TN 3178.Google Scholar
Laadhari, F. 2007 Reynolds number effect on the dissipation function in wall-bounded flows. Phys. Fluids 19, 038101.CrossRefGoogle Scholar
Laufer, J.1951 Investigation of turbulent flow in a two-dimensional channel. NACA Rept. 1053.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26, 011702.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
McKeon, B. J. & Morrison, J. F. 2007 Asymptotic scaling in turbulent pipe flow. Phil. Trans. R. Soc. Lond. A 365, 771–787.Google ScholarPubMed
McKeon, B. J., Swanson, C. J., Zagarola, M. V., Donnelly, R. J. & Smits, A. J. 2004 Friction factors for smooth pipe flow. J. Fluid Mech. 511, 41–44.CrossRefGoogle Scholar
Millikan, C. M. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the 5th Int. Congr. Appl. Mech., New York, pp. 386–392. Wiley.Google Scholar
Monty, J. P.2005 Developments in smooth wall turbulent duct flows. PhD thesis, University of Melbourne, Australia.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.CrossRefGoogle Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.CrossRefGoogle Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
Nikuradse, J.1932 Laws of turbulent flow in smooth pipes (English translation). NASA TT F-10 (1966).Google Scholar
Patel, V. C. & Head, M. R. 1969 Some observations on skin friction and velocity profiles in fully developed pipe and channel flows. J. Fluid Mech. 38, 181–201.CrossRefGoogle Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aeronaut. Sci. 2, 1–219.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Schultz, M. P. & Flack, K. A. 2013 Reynolds-number scaling of turbulent channel flow. Phys. Fluids 25 (2), 025104.CrossRefGoogle Scholar
Shah, D. A.1988 Scaling of the ‘bursting’ and ‘pulse’ periods in wall bounded turbulent flows. PhD thesis, University of Newcastle.Google Scholar
Sillero, J. A., Jimenez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25, 105102.CrossRefGoogle Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to R 𝜃 = 1410. J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
Sreenivasan, K. R. 1995 The energy dissipation in turbulent shear flows. In Symposium on Developments in Fluid Dynamics and Aerospace Engineering (ed. Deshpande, S. M., Prabhu, A., Sreenivasan, K. R. & Viswanath, P. R.), pp. 159–190. Interline Publishers.Google Scholar
Swanson, C. J., Julian, B., Ihas, G. G. & Donnelly, R. J. 2002 Pipe flow measurements over a wide range of Reynolds numbers using liquid helium and various gases. J. Fluid Mech. 461, 51–60.CrossRefGoogle Scholar
Tanahashi, M., Kang, S.-J., Miyamoto, T., Shiokawa, S. & Miyauchi, T. 2004 Scaling law of fine scale eddies in turbulent channel flows up to Re 𝜏 = 800. Intl J. Heat Fluid Flow 25, 331–340.CrossRefGoogle Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. III. Distribution of dissipation of energy in a pipe over its cross-section. Proc. R. Soc. Lond. A 151, 455–464.CrossRefGoogle Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11, 97–120.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. vol. 2. Cambridge University Press.Google Scholar
Tsukahara, T., Seki, Y., Kawamura, H. & Tochio, D. 2005 DNS of turbulent channel flow at very low Reynolds numbers. In Proceedings of the Fourth Int. Symp. on Turbulence and Shear Flow Phenomena, Williamsburg, USA, pp. 935–940.CrossRefGoogle Scholar
Vreman, A. W. & Kuerten, J. G. M. 2014 Statistics of spatial derivatives of velocity and pressure in turbulent channel flow. Phys. Fluids 26, 085103.CrossRefGoogle Scholar
Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 81–112.CrossRefGoogle Scholar
Zanoun, E.-S., Durst, F. & Nagib, H. 2003 Evaluating the law of the wall in two-dimensional fully developed turbulent channel flows. Phys. Fluids 15, 3079–3089.CrossRefGoogle Scholar
Zanoun, E.-S., Nagib, H. & Durst, F. 2009 Refined C f relation for turbulent channels and consequences for high Re experiments. Fluid Dyn. Res. 41, 1–12.CrossRefGoogle Scholar