Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-21T05:02:17.895Z Has data issue: false hasContentIssue false
  • English
  • Français

Rayleigh–Taylor unstable condensing liquid layers with nonlinear effects of interfacial convection and diffusion of vapour

Published online by Cambridge University Press:  06 October 2020

Tao Wei Open the ORCID record for Tao Wei [Opens in a new window]  and
Mengqi Zhang Open the ORCID record for Mengqi Zhang [Opens in a new window]
Tao Wei*
Affiliation:
School of Mechanical and Aerospace Engineering, Nanyang Technological University, 639798, Republic of Singapore Department of Mechanical Engineering, National University of Singapore, 117575, Republic of Singapore
Mengqi Zhang
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575, Republic of Singapore
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

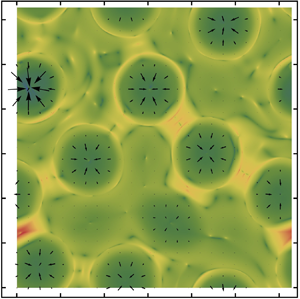
We investigate the three-dimensional surface pattern and nonlinear dynamics of a condensing liquid layer suspended from a cooled substrate and in contact with a mixture of its vapour and an inert gas below. A vapour boundary layer (VBL) is introduced, to which the changes in gaseous composition and temperature are assumed to be confined. An interfacial transport equation is derived, which incorporates the physical effects of convection and diffusion of vapour within the VBL, coupled with a long-wave evolution equation for the location of the free surface. This work extends the study of Kanatani (J. Fluid Mech., vol. 732, 2013, pp. 128–149) on a sessile evaporating film to the Rayleigh–Taylor unstable condensing/evaporating case with nonlinear analyses which also accounts for the effect of vapour recoil due to mass transfer on interfacial evolution and that of gravity combined with buoyancy on the internal convection of pendent drops in a condensate layer. The coupled nonlinear evolutionary system is referred to as a $1.5$-sided model. It can be reduced to the conventional one-sided model when phase change is limited by processes in the liquid. An extended basic state is obtained, whose stability is investigated with pseudo-steady linear theory and time-dependent nonlinear simulations. With the one-sided model, the influences of vapour recoil and Marangoni effects are illustrated with three representative cases. In the one-sided simulations with a random perturbation, the interface is prone to finite-time rupture and the surface patterns feature isolated droplets when vapour recoil is significant, while it becomes more regular and even without rupture as vapour recoil is weakened relative to the Marangoni effect. This suggests that, in the absence of the convection and diffusion of vapour, the destabilizations of vapour recoil and negative gravity could prevail over the stabilizations of thermocapillarity, capillarity, viscous dissipation and mass gain. With an unsaturated initial interface concentration, $\tilde {x}_{A,I0}$, the $1.5$-sided model indicates that the liquid layer can be stabilized to a quasi-hexagon pattern and the Rayleigh–Taylor-driven rupture can be suppressed with the effects of vapour convection and diffusion near the interface. However, the initial dynamics is in contrast to the case with a saturated $\tilde {x}_{A,I0}$, where transition from weak evaporation to a condensation-dominated regime is seen in the later stage. The viewpoint of stability competition offers vital evidence for an induced Marangoni stabilization, which is a quintessential characteristic of the $1.5$-sided model. Comparisons of the theory and simulations with available experiments are included throughout.

JFM classification

Phase change: Condensation/evaporation Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 904 , 10 December 2020 , A1
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alexeev, A. & Oron, A. 2007 Suppression of the Rayleigh–Taylor instability of thin liquid films by the Marangoni effect. Phys. Fluids 19, 082101.CrossRefGoogle Scholar
Benney, D. J. 1966 Long waves on liquid films. J. Math. Phys. 45, 150–155.CrossRefGoogle Scholar
Berg, J. C., Boudart, M. & Acrivos, A. 1966 Natural convection in pools of evaporating liquids. J. Fluid Mech. 24, 721–735.CrossRefGoogle Scholar
Bestehorn, M. & Merkt, D. 2006 Regular surface patterns on Rayleigh–Taylor unstable evaporating films heated from below. Phys. Rev. Lett. 97, 127802.CrossRefGoogle ScholarPubMed
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 2002 Transport Phenomena, 2nd edn. John Wiley & Sons.Google Scholar
Boomkamp, P. A. M. & Miesen, R. H. M. 1996 Classification of instabilities in parallel two-phase flow. Intl J. Multiphase Flow 22 (Suppl.), 67–88.CrossRefGoogle Scholar
Burelbach, J. P., Bankoff, S. G. & Davis, S. H. 1988 Nonlinear stability of evaporating/condensing liquid films. J. Fluid Mech. 195, 463–494.CrossRefGoogle Scholar
Burgess, J. M., Juel, A., McCormick, W. D., Swift, J. B. & Swinney, H. L. 2001 Suppression of dripping from a ceiling. Phys. Rev. Lett. 86, 1203–1206.CrossRefGoogle ScholarPubMed
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Chauvet, F., Dehaeck, S. & Colinet, P. 2012 Threshold of Bénard–Marangoni instability in drying liquid films. Europhys. Lett. 99, 34001.CrossRefGoogle Scholar
Dehaeck, S., Rednikov, A. & Colinet, P. 2014 Vapor-based interferometric measurement of local evaporation rate and interfacial temperature of evaporating droplets. Langmuir 30, 2002–2008.CrossRefGoogle ScholarPubMed
Deissler, R. J. & Oron, A. 1992 Stable localized patterns in thin liquid films. Phys. Rev. Lett. 68, 2948–2951.CrossRefGoogle ScholarPubMed
Dittmar, D., Fredenhagen, A., Oei, S. B. & Eggers, R. 2003 Interfacial tensions of ethanol-carbon dioxide and ethanol-nitrogen. Dependence of the interfacial tension on the fluid density–prerequisites and physical reasoning. Chem. Engng Sci. 58, 1223–1233.CrossRefGoogle Scholar
Doumenc, F., Boeck, T., Guerrier, B. & Rossi, M. 2010 Transient Rayleigh–Bénard–Marangoni convection due to evaporation: a linear non-normal stability analysis. J. Fluid Mech. 648, 521–539.CrossRefGoogle Scholar
Ehrhard, P. & Davis, S. H. 1991 Non-isothermal spreading of liquid drops on horizontal plates. J. Fluid Mech. 229, 365–388.CrossRefGoogle Scholar
Fermigier, M., Limat, L., Wesfreid, J. E., Boudinet, P. & Quilliet, C. 1992 Two-dimensional patterns in Rayleigh–Taylor instability of a thin layer. J. Fluid Mech. 236, 349–383.CrossRefGoogle Scholar
Fujii, T. 1991 Theory of Laminar Film Condensation. Springer.CrossRefGoogle Scholar
Gerstmann, J. & Griffith, P. 1965 The effects of surface instabilities on laminar film condensation. Tech. Rep. 5050-36. Department of Mechanical Engineering, MIT.Google Scholar
Gerstmann, J. & Griffith, P. 1967 Laminar film condensation on the underside of horizontal and inclined surfaces. Intl J. Heat Mass Transfer 10, 567–580.CrossRefGoogle Scholar
Guo, W. & Narayanan, R. 2010 Interfacial instability due to evaporation and convection: linear and nonlinear analyses. J. Fluid Mech. 650, 363–389.CrossRefGoogle Scholar
Hammond, P. S. 1983 Nonlinear adjustment of a thin annular film of viscous fluid surrounding a thread of another within a circular cylindrical pipe. J. Fluid Mech. 137, 363–384.CrossRefGoogle Scholar
Haut, B. & Colinet, P. 2005 Surface-tension-driven instabilities of a pure liquid layer evaporating into an inert gas. J. Colloid Interface Sci. 285, 296–305.CrossRefGoogle ScholarPubMed
Hickman, K. C. D. 1952 Surface behavior in the pot still. Ind. Engng Chem. 44, 1892–1902.CrossRefGoogle Scholar
Hsieh, D. Y. 1972 Effects of heat and mass transfer on Rayleigh–Taylor instability. Trans. ASME: J. Basic Engng 94, 156–160.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Kanatani, K. 2010 Interfacial instability induced by lateral vapor pressure fluctuation in bounded thin liquid-vapor layers. Phys. Fluids 22, 012101.CrossRefGoogle Scholar
Kanatani, K. 2013 Effects of convection and diffusion of the vapour in evaporating liquid films. J. Fluid Mech. 732, 128–149.CrossRefGoogle Scholar
Kanatani, K. & Oron, A. 2011 Nonlinear dynamics of confined thin liquid-vapor bilayer systems with phase change. Phys. Fluids 23, 032102.CrossRefGoogle Scholar
Kimball, J. T., Hermanson, J. C. & Allen, J. S. 2012 Experimental investigation of convective structure evolution and heat transfer in quasi-steady evaporating liquid films. Phys. Fluids 24, 052102.CrossRefGoogle Scholar
Kliakhandler, I. L., Davis, S. H. & Bankoff, S. G. 2002 The effect of heat conduction in the vapor on the dynamics of downflowing condensate. Phys. Fluids 14, 150–157.CrossRefGoogle Scholar
Kroger, D. G. & Rohsenow, W. M. 1968 Condensation heat transfer in the presence of a non-condensable gas. Intl J. Heat Mass Transfer 11, 15–26.CrossRefGoogle Scholar
Margerit, J., Dondlinger, M. & Dauby, P. C. 2005 Improved 1.5-sided model for the weakly nonlinear study of Bénard–Marangoni instabilities in an evaporating liquid layer. J. Colloid Interface Sci. 290, 220–230.CrossRefGoogle Scholar
Oron, A. 2000 a Nonlinear dynamics of three-dimensional long-wave Marangoni instability in thin liquid films. Phys. Fluids 12, 1633–1645.CrossRefGoogle Scholar
Oron, A. 2000 b Three-dimensional nonlinear dynamics of thin liquid films. Phys. Rev. Lett. 85, 2108–2111.CrossRefGoogle ScholarPubMed
Oron, A. & Bankoff, S. G. 2001 Dynamics of a condensing liquid film under conjoining/disjoining pressures. Phys. Fluids 13, 1107–1117.CrossRefGoogle Scholar
Oron, A., Davis, S. H. & Bankoff, S. G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980.CrossRefGoogle Scholar
Oron, A. & Rosenau, P. 1992 Formation of patterns induced by thermocapillarity and gravity. J. Phys. II France 2, 131–146.CrossRefGoogle Scholar
Palmer, H. J. 1976 The hydrodynamic stability of rapidly evaporating liquids at reduced pressure. J. Fluid Mech. 75, 487–511.CrossRefGoogle Scholar
Palmer, H. J. & Maheshri, J. C. 1981 Enhanced interfacial heat transfer by differential vapor recoil instabilities. Intl J. Heat Mass Transfer 4, 117–123.CrossRefGoogle Scholar
Panzarella, C. H., Davis, S. H. & Bankoff, S. G. 2000 Nonlinear dynamics in horizontal film boiling. J. Fluid Mech. 402, 163–194.CrossRefGoogle Scholar
Pillai, D. S. & Narayanan, R. 2018 Rayleigh–Taylor stability in an evaporating binary mixture. J. Fluid Mech. 848, R1.CrossRefGoogle Scholar
Radhakrishnan, K. & Hindmarsh, A. C. 1993 Description and use of LSODE, the Livermore solver for ordinary differential equations. Tech. Rep. 1327. NASA Reference Publication.CrossRefGoogle Scholar
Savino, R., Paterna, D. & Favaloro, N. 2002 Buoyancy and Marangoni effects in an evaporating drop. J. Thermophys. Heat Transfer 16, 562–574.CrossRefGoogle Scholar
Schrage, R. W. 1953 A Theoretical Study of Interphase Mass Transfer. Columbia University PressCrossRefGoogle Scholar
Som, S. M., Kimball, J. T., Hermanson, J. C. & Allen, J. S. 2007 Stability and heat transfer characteristics of unsteady condensing and evaporating films. Intl J. Heat Mass Transfer 50, 1927–1937.CrossRefGoogle Scholar
Sultan, E., Boudaoud, A. & Amar, M. B. 2005 Evaporation of a thin film: diffusion of the vapour and Marangoni instabilities. J. Fluid Mech. 543, 183–202.CrossRefGoogle Scholar
Velarde, M. G., Nepomnyashchy, A. A. & Hennenberg, M. 2001 Onset of oscillatory interfacial instability and wave motions in Bénard layers. Adv. Appl. Mech. 37, 167–238.CrossRefGoogle Scholar
Ward, C. A. & Stanga, D. 2001 Interfacial conditions during evaporation or condensation of water. Phys. Rev. E 64, 051509.CrossRefGoogle ScholarPubMed
Wei, T. & Duan, F. 2016 Interfacial stability and self-similar rupture of evaporating liquid layers under vapor recoil. Phys. Fluids 28, 124106.CrossRefGoogle Scholar
Wei, T. & Duan, F. 2018 Long-wave-instability-induced pattern formation in an evaporating sessile or pendent liquid layer. Phys. Rev. Fluids 3, 034001.CrossRefGoogle Scholar
Wolf, G. H. 1970 Dynamic stabilization of the interchange instability of a liquid–gas interface. Phys. Rev. Lett. 24, 444–446.CrossRefGoogle Scholar
Yanadori, M., Hijikata, K., Mori, Y. & Uchida, M. 1985 Fundamental study of laminar film condensation heat transfer on a downward horizontal surface. Intl J. Heat Mass Transfer 28, 1937–1944.Google Scholar
Yiantsios, S. G. & Higgins, B. G. 1989 Rayleigh–Taylor instability in thin viscous films. Phys. Fluids A 1, 1484–1501.CrossRefGoogle Scholar
Yih, C. S. 1955 Stability of two-dimensional parallel flows for three-dimensional disturbances. Q. Appl. Maths 12, 434–435.CrossRefGoogle Scholar
Zhang, N. 2006 Surface tension-driven convection flow in evaporating liquid layers. In Surface Tension-Driven Flows and Applications (ed. Savino, R.), pp. 147–171. Research Signpost.Google Scholar