Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zhou, Ye
2017.
Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I.
Physics Reports,
Vol. 720-722,
Issue. ,
p.
1.
Morgan, R. V.
Cabot, W. H.
Greenough, J. A.
and
Jacobs, J. W.
2018.
Rarefaction-driven Rayleigh–Taylor instability. Part 2. Experiments and simulations in the nonlinear regime.
Journal of Fluid Mechanics,
Vol. 838,
Issue. ,
p.
320.
Patterson, Brandon
and
Johnsen, Eric
2018.
Growth of liquid-gas interfacial perturbations driven by acoustic waves.
Physical Review Fluids,
Vol. 3,
Issue. 7,
Olsthoorn, Jason
Tedford, Edmund W.
and
Lawrence, Gregory A.
2019.
Diffused-interface Rayleigh-Taylor instability with a nonlinear equation of state.
Physical Review Fluids,
Vol. 4,
Issue. 9,
Hu, Ze-Xi
Zhang, You-Sheng
Tian, Baolin
He, Zhiwei
and
Li, Li
2019.
Effect of viscosity on two-dimensional single-mode Rayleigh-Taylor instability during and after the reacceleration stage.
Physics of Fluids,
Vol. 31,
Issue. 10,
González-Gutiérrez, L. M.
and
de Andrea González, A.
2019.
Numerical computation of the Rayleigh-Taylor instability for a viscous fluid with regularized interface properties.
Physical Review E,
Vol. 100,
Issue. 1,
Liang, Yu
Zhai, Zhigang
Luo, Xisheng
and
Wen, Chih-yung
2020.
Interfacial instability at a heavy/light interface induced by rarefaction waves.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Banerjee, Arindam
2020.
Rayleigh-Taylor Instability: A Status Review of Experimental Designs and Measurement Diagnostics.
Journal of Fluids Engineering,
Vol. 142,
Issue. 12,
Hu, Ze-Xi
Zhang, You-sheng
and
Tian, Bao-lin
2020.
Evolution of Rayleigh-Taylor instability under interface discontinuous acceleration induced by radiation.
Physical Review E,
Vol. 101,
Issue. 4,
Fan, Zhengfeng
and
Dong, Ming
2020.
Multiple eigenmodes of the Rayleigh-Taylor instability observed for a fluid interface with smoothly varying density. III. Excitation and nonlinear evolution.
Physical Review E,
Vol. 101,
Issue. 6,
Luo, Tengfei
Wang, Jianchun
Xie, Chenyue
Wan, Minping
and
Chen, Shiyi
2020.
Effects of compressibility and Atwood number on the single-mode Rayleigh-Taylor instability.
Physics of Fluids,
Vol. 32,
Issue. 1,
Liang, Yu
Liu, Lili
Zhai, Zhigang
Si, Ting
and
Wen, Chih-Yung
2020.
Evolution of shock-accelerated heavy gas layer.
Journal of Fluid Mechanics,
Vol. 886,
Issue. ,
Mansoor, M. M.
Dalton, S. M.
Martinez, A. A.
Desjardins, T.
Charonko, J. J.
and
Prestridge, K. P.
2020.
The effect of initial conditions on mixing transition of the Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Martinez-Carrascal, Jon
Calderon-Sanchez, J.
González-Gutiérrez, L. M.
and
de Andrea González, A.
2021.
Extended computation of the viscous Rayleigh-Taylor instability in a horizontally confined flow.
Physical Review E,
Vol. 103,
Issue. 5,
Mukhopadhyay, Sourabh
and
Nimbalkar, Ganesh
2021.
Fundamental study on chaotic transition of two-phase flow regime and free surface instability in gas deaeration process.
Experimental and Computational Multiphase Flow,
Vol. 3,
Issue. 4,
p.
258.
Liang, Yu
and
Luo, Xisheng
2021.
On shock-induced heavy-fluid-layer evolution.
Journal of Fluid Mechanics,
Vol. 920,
Issue. ,
Song, Yang
Wang, Pei
Wang, Lili
Ma, Dongjun
He, Anmin
Chen, Dawei
Fan, Zhengfeng
Ma, Zongqiang
and
Wang, Jianguo
2021.
The early-time dynamics of Rayleigh-Taylor mixing with a premixed layer.
Computers & Fluids,
Vol. 229,
Issue. ,
p.
105061.
Livescu, D.
Wei, T.
and
Brady, P.T.
2021.
Rayleigh–Taylor instability with gravity reversal.
Physica D: Nonlinear Phenomena,
Vol. 417,
Issue. ,
p.
132832.
Li, Lei
Lu, Xiao-xia
Ren, Xiao-bin
Ren, Ye-jun
Zhao, Shou-tian
and
Yan, Xiao-fang
2021.
The mechanism of liquid dispersing from a cylinder driven by central dynamic shock loading.
Defence Technology,
Vol. 17,
Issue. 4,
p.
1313.
Li, Haifeng
Tian, Baolin
He, Zhiwei
and
Zhang, Yousheng
2021.
Growth mechanism of interfacial fluid-mixing width induced by successive nonlinear wave interactions.
Physical Review E,
Vol. 103,
Issue. 5,
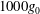 $1000g_{0}$, where
$1000g_{0}$, where 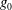 $g_{0}$ is the acceleration due to gravity. Initial interface thicknesses are measured using a Rayleigh scattering diagnostic and the instability is visualized using planar laser-induced Mie scattering. Growth rates agree well with theoretical values, and with the inviscid, dynamic diffusion model of Duff et al. (Phys. Fluids, vol. 5, 1962, pp. 417–425) when diffusion thickness is accounted for, and the acceleration is weighted using inviscid Rayleigh–Taylor theory. The linear stability formulation of Chandrasekhar (Proc. Camb. Phil. Soc., vol. 51, 1955, pp. 162–178) is solved numerically with an error function diffusion profile using the Riccati method. This technique exhibits good agreement with the dynamic diffusion model of Duff et al. for small wavenumbers, but produces larger growth rates for large-wavenumber perturbations. Asymptotic analysis shows a
$g_{0}$ is the acceleration due to gravity. Initial interface thicknesses are measured using a Rayleigh scattering diagnostic and the instability is visualized using planar laser-induced Mie scattering. Growth rates agree well with theoretical values, and with the inviscid, dynamic diffusion model of Duff et al. (Phys. Fluids, vol. 5, 1962, pp. 417–425) when diffusion thickness is accounted for, and the acceleration is weighted using inviscid Rayleigh–Taylor theory. The linear stability formulation of Chandrasekhar (Proc. Camb. Phil. Soc., vol. 51, 1955, pp. 162–178) is solved numerically with an error function diffusion profile using the Riccati method. This technique exhibits good agreement with the dynamic diffusion model of Duff et al. for small wavenumbers, but produces larger growth rates for large-wavenumber perturbations. Asymptotic analysis shows a 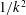 $1/k^{2}$ decay in growth rates as
$1/k^{2}$ decay in growth rates as 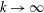 $k\rightarrow \infty$ for large-wavenumber perturbations.
$k\rightarrow \infty$ for large-wavenumber perturbations.


