Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T15:15:52.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-geostrophic approximation of anelastic convection

Published online by Cambridge University Press:  18 June 2014

Friedrich H. Busse  and
Radostin D. Simitev
Friedrich H. Busse*
Affiliation:
Institute of Physics, University of Bayreuth, 95440 Bayreuth, Germany Earth and Space Sciences, University of California–Los Angeles, Los Angeles, CA 90095, USA
Radostin D. Simitev
Affiliation:
School of Mathematics and Statistics, University of Glasgow, Glasgow G12 8QW, UK Earth and Space Sciences, University of California–Los Angeles, Los Angeles, CA 90095, USA Hansen Experimental Physics Laboratory, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The onset of convection in a rotating cylindrical annulus with parallel ends filled with a compressible fluid is studied in the anelastic approximation. Thermal Rossby waves propagating in the azimuthal direction are found as solutions. The analogy to the case of Boussinesq convection in the presence of conical end surfaces of the annular region is emphasised. As in the latter case, the results can be applied as an approximation for the description of the onset of anelastic convection in rotating spherical fluid shells. Reasonable agreement with three-dimensional numerical results published by Jones, Kuzanyan & Mitchell (J. Fluid Mech., vol. 634, 2009, pp. 291–319) for the latter problem is found. As in those results, the location of the onset of convection shifts outwards from the tangent cylinder with increasing number 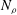$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}N_{\rho }$ of density scale heights until it reaches the equatorial boundary. A new result is that at a much higher number 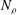$N_{\rho }$ the onset location returns to the interior of the fluid shell.

JFM classification

Convection: Convection Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 216 - 227
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Braginsky, S. I. & Roberts, P. H. 1995 Equations governing convection in Earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 79, 1–97.Google Scholar
Busse, F. H. 1970 Thermal instabilities in rapidly rotating cylindrical annulus. J. Fluid Mech. 44, 441–460.Google Scholar
Busse, F. H. 1983 A model of mean zonal flows in the major planets. Geophys. Astrophys. Fluid Dyn. 23, 153–174.CrossRefGoogle Scholar
Busse, F. H. 1986 Asymptotic theory of convection in a rotating, cylindrical annulus. J. Fluid Mech. 173, 545–556.CrossRefGoogle Scholar
Busse, F. H. 2002 Convective flows in rapidly rotating spheres and their dynamo action. Phys. Fluids 14, 1301–1314.CrossRefGoogle Scholar
Busse, F. H. & Or, A. C. 1986 Convection in a rotating cylindrical annulus: thermal Rossby waves. J. Fluid Mech. 166, 173–187.CrossRefGoogle Scholar
Calkins, M., Julien, K. & Marti, P. 2013 Three-dimensional quasi-geostrophic convection in the rotating cylindrical annulus with steeply sloping endwalls. J. Fluid Mech. 732, 214–244.CrossRefGoogle Scholar
Evonuk, M. & Glatzmaier, G. A. 2004 2D studies of various approximations used for modeling convection in giant planets. Geophys. Astrophys. Fluid Dyn. 98, 241–255.CrossRefGoogle Scholar
Evonuk, M. & Glatzmaier, G. A. 2006 A 2D study of the effects of the size of a solid core on the equatorial flow in giant planets. Icarus 181, 458–464.Google Scholar
Gastine, T. & Wicht, J. 2012 Effects of compressibility on driving zonal flows in gas giants. Icarus 219, 428–442.Google Scholar
Gillet, N. & Jones, C. A. 2006 The quasi-geostrophic model for rapidly rotating spherical convection outside the tangent cylinder. J. Fluid Mech. 554, 343–369.Google Scholar
Glatzmaier, G. A., Evonuk, M. & Rogers, T. M. 2009 Differential rotation in giant planets maintained by density-stratified turbulent convection. Geophys. Astrophys. Fluid Dyn. 103, 31–51.CrossRefGoogle Scholar
Gough, D. O. 1969 The anelastic approximation for thermal convection. J. Atmos. Sci. 26, 448–456.Google Scholar
Jones, C. A., Boronski, P., Brun, A. S., Glatzmaier, G. A., Gastine, T., Miesch, M. S. & Wicht, J. 2011 Anelastic convection-driven dynamo benchmarks. Icarus 216, 120–135.Google Scholar
Jones, C. A., Kuzanyan, K. M. & Mitchell, R. H. 2009 Linear theory of compressible convection in rapidly rotating spherical shells, using the anelastic approximation. J. Fluid Mech. 634, 291–319.Google Scholar
Lantz, S. R. & Fan, Y. 1999 Anelastic magnetohydrodynamic equations for modeling solar and stellar convection zones. Astrophys. J. Suppl. 121, 247–264.Google Scholar
Simitev, R. D. & Busse, F. H. 2003 Patterns of convection in rotating spherical shells. New J. Phys. 5, 97.1–97.20.Google Scholar