Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-22T13:09:00.828Z Has data issue: false hasContentIssue false
  • English
  • Français

Pulsed jets driven by two interacting cavitation bubbles produced at different times

Published online by Cambridge University Press:  27 April 2017

Y. Tomita  and
K. Sato Open the ORCID record for K. Sato [Opens in a new window]
Y. Tomita
Affiliation:
Faculty of Education, Hokkaido University of Education, Hakodate 040-8567, Japan
K. Sato*
Affiliation:
Faculty of Engineering, Kogakuin University, Hachioji, Tokyo 192-0015, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

An experiment is performed using high-speed photography to elucidate the behaviours of jets formed by the interactions of two laser-induced tandem bubbles produced axisymmetrically for a range of dimensionless interaction parameters such as the bubble size ratio, 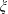$\unicode[STIX]{x1D709}$, the distance between the two cavitation bubbles, 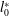$l_{0}^{\ast }$, and the time difference in bubble generation, 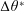$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}^{\ast }$. A strong interaction occurs for 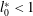$l_{0}^{\ast }<1$. The first bubble produced (bubble A) deforms because of the rapid growth of the second bubble (bubble B) to create a pulsed conical jet, sometimes with spray formation at the tip, formed by the small amount of water confined between the two bubbles. This phenomenon is followed by bubble penetration, toroidal bubble collapse, and the subsequent fast contraction of bubble B accompanied by a fine jet. The formation mechanism of the conical jet is similar to that of a water spike developed in air from a deformed free surface of a single growing bubble; however, the pressures of the gases surrounding each type of jet differ. The jet behaviours can be controlled by manipulating the interaction parameters; the jet velocity is significantly affected by 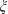$\unicode[STIX]{x1D709}$ and 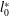$l_{0}^{\ast }$, but less so by 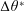$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}^{\ast }$ for 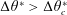$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}^{\ast }>\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{c}^{\ast }$ (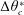$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}_{c}^{\ast }$ being the critical birth-time difference). The optimum time of jet impact, at which bubble A reaches its maximum volume, depends on 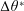$\unicode[STIX]{x0394}\unicode[STIX]{x1D703}^{\ast }$. It is generally later for larger values of 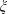$\unicode[STIX]{x1D709}$. A pulsed jet could be used to create small pores in a cell membrane; therefore, the reported method may be useful for application in tandem-bubble sonoporation.

JFM classification

Drops and Bubbles: Bubble dynamics Drops and Bubbles: Cavitation Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 819 , 25 May 2017 , pp. 465 - 493
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bao, S., Thrall, B. D. & Miller, D. L. 1997 Transfection of a reporter plasmid into cultured cells by sonoporation in vitro . Ultrasound Med. Biol. 23, 953–959.CrossRefGoogle ScholarPubMed
Blake, J. R. & Gibson, D. C. 1981 Growth and collapse of a vapour cavity near a free surface. J. Fluid Mech. 111, 123–140.Google Scholar
Blake, J. R. & Gibson, D. C. 1987 Cavitation bubbles near boundaries. Annu. Rev. Fluid Mech. 19, 99–123.CrossRefGoogle Scholar
Blake, J. R., Keen, G. S., Tong, R. P. & Wilson, M. 1999 Acoustic cavitation: the fluid dynamics of non-spherical bubbles. Phil. Trans. R. Soc. Lond. A 357, 251–267.Google Scholar
Blake, J. R., Leppinen, D. M. & Wang, Q. 2015 Cavitation and bubble dynamics: the Kelvin impulse and its applications. Interface Focus 5, 20150017.CrossRefGoogle ScholarPubMed
Blake, J. R., Robinson, P. B., Shima, A. & Tomita, Y. 1993 Interaction of two cavitation bubbles with a rigid boundary. J. Fluid Mech. 255, 707–721.Google Scholar
Brujan, E. A., Nahen, K., Schmidt, P. & Vogel, A. 2001 Dynamics of laser-induced cavitation bubbles near an elastic boundary. J. Fluid Mech. 433, 251–281.CrossRefGoogle Scholar
Chen, R. C. C., Yu, Y. T., Su, K. W., Chen, J. F. & Chen, Y. F. 2013 Exploration of water jet generated by Q-switched laser induced water breakdown with different depths beneath a flat free surface. Opt. Express 21, 445–453.CrossRefGoogle ScholarPubMed
Chew, L. W., Klaseboer, E., Ohl, S.-W. & Khoo, B. C. 2011 Interaction of two differently sized oscillating bubbles in a free field. Phys. Rev. E 84, 066307.Google Scholar
Crum, L. A. 1975 Bjerknes forces on bubbles in a stationary sound field. J. Acoust. Soc. Am. 57, 1363–1370.Google Scholar
Dear, J. P. & Field, J. E. 1988 A study of the collapse of arrays of cavities. J. Fluid Mech. 190, 409–425.Google Scholar
Fong, S. W., Adhikari, D., Klaseboer, E. & Khoo, B. C. 2009 Interactions of multiple spark-generated bubbles with phase differences. Exp. Fluids 46, 705–724.Google Scholar
Forbes, M. M., Steinberg, R. L. & O’Brien, W. D. Jr. 2008 Examination of inertial cavitation of Optison™ in producing sonoporation of Chinese hamster ovary cells. Ultrasound Med. Biol. 34, 2009–2018.Google Scholar
Gekle, S. & Gordillo, J. M. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 1. Jet formation. J. Fluid Mech. 663, 293–330.CrossRefGoogle Scholar
Gibson, D. C. 1968 Cavitation adjacent to plane boundaries. In Proceedings of the 3rd Australasian Conference on Hydraulics and Fluid Mechanics, pp. 210–214. Institution of Engineers.Google Scholar
Gordillo, J. M. & Gekle, S. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 2. Tip breakup of stretched jets. J. Fluid Mech. 663, 331–346.Google Scholar
Gregorčič, P., Petkovšek, R. & Možina, J. 2007 Investigation of a cavitation bubble between a rigid boundary and a free surface. J. Appl. Phys. 102, 094904.Google Scholar
Han, B., Köhler, K., Jungnickel, K., Mettin, R., Lauterborn, W. & Vogel, A. 2015 Dynamics of laser-induced bubble pairs. J. Fluid Mech. 771, 706–742.Google Scholar
Harkin, A., Kaper, T. J. & Nadim, A. 2001 Coupled pulsation and translation of two gas bubbles in a liquid. J. Fluid Mech. 445, 377–411.Google Scholar
Heymann, F. J. 1968 On the shock wave velocity and impact pressure in high-speed liquid–solid impact. Trans. ASME J. Basic Engng 90, 400–402.Google Scholar
Hsiao, C.-T., Choi, J.-K., Singh, S., Chahine, G. L., Hay, T. A., Ilinskii, Y. A., Zabolotskaya, E. A., Hamilton, M. F., Sankin, G., Yuan, F. & Zhong, P. 2013 Modelling single- and tandem-bubble dynamics between two parallel plates for biomedical applications. J. Fluid Mech. 716, 137–170.Google Scholar
Johnsen, E. & Colonius, T. 2009 Numerical simulations of non-spherical bubble collapse. J. Fluid Mech. 629, 231–262.Google Scholar
Jungnickel, K. & Vogel, A. 1994 Interaction of two laser–induced cavitation bubbles. In Bubble Dynamics and Interface Phenomena (ed. Blake, J. R., Boulton-Stone, J. M. & Thomas, N. H.), Fluid Mechanics and Its Applications, vol. 23, pp. 47–53. Kluwer.Google Scholar
Kobayashi, K., Kodama, T. & Takahira, H. 2011 Shock wave-bubble interaction near soft and rigid boundaries during lithotripsy: numerical analysis by the improved ghost fluid method. Phys. Med. Biol. 56, 6421–6440.CrossRefGoogle ScholarPubMed
Kodama, T.1992 Study on cavitation bubbles near deformable boundaries. Doctoral thesis, Tohoku University, 69.Google Scholar
Lauterborn, W. & Hentschel, W. 1985 Cavitation bubble dynamics studied by high speed photography and holography: part one. Ultrasonics 23, 260–268.Google Scholar
Longuet-Higgins, M. S. 1983 Bubbles, breaking waves and hyperbolic jets at a free surface. J. Fluid Mech. 127, 103–121.Google Scholar
Naudé, C. F. & Ellis, A. T. 1961 On the mechanism of cavitation damage by nonhemispherical cavities collapsing in contact with a solid boundary. Trans. ASME D: J. Basic Engng 83, 648–656.CrossRefGoogle Scholar
Obreschkow, D., Kobel, P., Dorsaz, N., de Bosset, A., Nicollier, C. & Farhat, M. 2006 Cavitation bubble dynamics inside liquid drops in microgravity. Phys. Rev. Lett. 97, 094502.CrossRefGoogle ScholarPubMed
Pearson, A.2002 Hydrodynamics of jet impact in a collapsing bubble. Doctoral thesis, The University of Birmingham, 192–204.Google Scholar
Pearson, A., Cox, E., Blake, J. R. & Otto, S. R. 2004 Bubble interactions near a free surface. Engng Anal. Bound. Elem. 28, 295–313.Google Scholar
Pelekasis, N. A. & Tsamopoulos, J. A. 1993 Bjerknes forces between two bubbles. Part 1. Response to a step change in pressure. J. Fluid Mech. 254, 467–499.Google Scholar
Philipp, A. & Lauterborn, W. 1998 Cavitation erosion by single laser-produced bubbles. J. Fluid Mech. 361, 75–116.Google Scholar
Postema, M., van Wamel, A., Lancée, C. T. & de Jong, N. 2004 Ultrasound-induced encapsulated microbubble phenomena. Ultrasound Med. Biol. 30, 827–840.CrossRefGoogle ScholarPubMed
Prentice, P., Cuschieri, A., Dholakia, K., Prausnitz, M. & Campbell, P. 2005 Membrane disruption by optically controlled microbubble cavitation. Nat. Phys. 1, 107–110.Google Scholar
Pumphrey, H. C. & Elmore, P. A. 1990 The entrainment of bubbles by drop impacts. J. Fluid Mech. 220, 539–567.CrossRefGoogle Scholar
Rayleigh, Lord 1917 On the pressure developed in a liquid during the collapse of a spherical cavity. Phil. Mag. 34, 94–98.CrossRefGoogle Scholar
Robert, E., Lettry, J., Farhat, M., Monkewitz, P. A. & Avellan, F. 2007 Cavitation bubble behavior inside a liquid jet. Phys. Fluids 19, 067106.Google Scholar
Robinson, P. B., Blake, J. R., Kodama, T., Shima, A. & Tomita, Y. 2001 Interaction of cavitation bubbles with a free surface. J. Appl. Phys. 89, 8225–8237.Google Scholar
Rotsch, C., Jacobson, K. & Radmacher, M. 1999 Dimensional and mechanical dynamics of active and stable edges in motile fibroblasts investigated by using atomic force microscopy. Proc. Natl Acad. Sci. USA 96, 921–926.CrossRefGoogle ScholarPubMed
Sankin, G. N., Yuan, F. & Zhong, P. 2010 Pulsating tandem microbubble for localized and directional single-cell membrane poration. Phys. Rev. Lett. 105, 078101.CrossRefGoogle ScholarPubMed
Sato, K., Tomita, Y. & Shima, A. 1994 Interaction of two bubbles produced with time difference. In The 29th Cavitation and Multiphase Flow Forum, Lake Tahoe, Nevada, USA (ed. Katz, J.), vol. 194, pp. 1–5. ASME-PUBLICATIONS-FED.Google Scholar
Sato, K., Tomita, Y. & Shima, A. 1998 Non-spherical motion of two cavitation bubbles produced with/without time delay near a boundary. In Proceedings of the 3rd International Symposium on Cavitation, Grenoble (ed. Michel, J. M. & Kato, H.), pp. 63–68.Google Scholar
Shima, A. 1971 The natural frequencies of two spherical bubbles oscillating in water. Trans. ASME J. Basic Engng 93, 426–431.Google Scholar
Testud-Giovanneschi, P., Alloncle, A. P. & Dufresne, D. 1990 Collective effects of cavitation: experimental study of bubble–bubble and bubble–shock wave interactions. J. Appl. Phys. 67, 3560–3564.CrossRefGoogle Scholar
Tinne, N., Knoop, G., Kallweit, N., Veith, S., Bleeker, S., Lubatschowski, H., Krüger, A. & Ripken, T. 2014 Effects of cavitation bubble interaction with temporally separated fs-laser pulses. J. Biomed. Opt. 19, 048001.Google Scholar
Tinne, N., Schumacher, S., Nuzzo, V., Arnold, C., Lubatschowski, H. & Ripken, T. 2010 Interaction dynamics of spatially separated cavitation bubbles in water. J. Biomed. Opt. 15, 068003.CrossRefGoogle ScholarPubMed
Tomita, Y. & Kodama, T. 2001 Some aspects of the motion of two laser-produced cavitation bubbles near a free surface. In IUTAM Symposium on Free Surface Flows (ed. King, A. C. & Shikhmurzaev, Y. D.), Fluid Mechanics and Its Applications, vol. 62, pp. 303–310. Kluwer.Google Scholar
Tomita, Y., Kodama, T. & Shima, A. 1991 Secondary cavitation due to interaction of a collapsing bubble with a rising free surface. Appl. Phys. Lett. 59, 274–276.Google Scholar
Tomita, Y., Matsuura, T. & Kodama, T. 2015 Temporal effect of inertial cavitation with and without microbubbles on surface deformation of agarose S gel in the presence of 1-MHz focused ultrasound. Ultrasonics 55, 1–5.Google Scholar
Tomita, Y., Robinson, P. B., Tong, R. P. & Blake, J. R. 2002 Growth and collapse of cavitation bubbles near a curved rigid boundary. J. Fluid Mech. 466, 259–283.Google Scholar
Tomita, Y., Saito, T. & Ganbara, S. 2007 Surface breakup and air bubble formation by drop impact in the irregular entrainment region. J. Fluid Mech. 588, 131–152.Google Scholar
Tomita, Y. & Sato, K. 2000 The behavior of two laser-produced cavitation bubbles near a solid boundary. In Proceedings of the Fifth International Conference on Hydraulic Machinery and Hydrodynamics, Timisoara (ed. Balasoiu, V. & Popoviciu, M.), vol. 1, pp. 249–256.Google Scholar
Tomita, Y., Sato, K. & Shima, A. 1994 Interaction of two laser-produced cavitation bubbles near boundaries. In Bubble Dynamics and Interface Phenomena (ed. Blake, J. R., Boulton-Stone, J. M. & Thomas, N. H.), Fluid Mechanics and Its Applications, vol. 23, pp. 33–45. Kluwer.Google Scholar
Tomita, Y. & Shima, A. 1986 Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J. Fluid Mech. 169, 535–564.CrossRefGoogle Scholar
Tomita, Y. & Shima, A. 1990 High-speed photographic observations of laser-induced cavitation bubbles in water. Acustica 71, 161–171.Google Scholar
Tomita, Y., Shima, A. & Sato, K. 1990 Dynamic behavior of two-laser-induced bubbles in water. Appl. Phys. Lett. 57, 234–237.CrossRefGoogle Scholar
Tomita, Y., Tsubota, M. & An-Naka, N. 2003 Energy evaluation of cavitation bubble generation and shock wave emission by laser focusing in liquid nitrogen. J. Appl. Phys. 93, 3039–3048.Google Scholar
Tong, R. P., Schiffers, W. P., Shaw, S. J., Blake, J. R. & Emmony, D. C. 1999 The role of ‘splashing’ in the collapse of a laser-generated cavity near a rigid boundary. J. Fluid Mech. 380, 339–361.Google Scholar
Tulin, M. P. 1969 On the creation of ultra-jets. In L. I. Sedov 60th Anniversary Volume: Problems of Hydrodynamics and Continuum Mechanics, Moscow, pp. 725–747.Google Scholar
Vogel, A., Lauterborn, W. & Timm, R. 1989 Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary. J. Fluid Mech. 206, 299–338.Google Scholar
Yuan, F., Sankin, G. & Zhong, P. 2011 Dynamics of tandem bubble interaction in a microfluidic channel. J. Acoust. Soc. Am. 130, 3339–3346.Google Scholar