Article contents
Proper orthogonal decomposition analysis and modelling of large-scale flow reorientations in a cubic Rayleigh–Bénard cell
Published online by Cambridge University Press: 24 October 2019
Abstract
This paper investigates the large-scale flow reorientations of Rayleigh–Bénard convection in a cubic cell using proper orthogonal decomposition (POD) analysis and modelling. A direct numerical simulation is performed for air at a Rayleigh number of 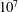 $10^{7}$ and shows that the flow is characterized by four quasi-stable states, corresponding to a large-scale circulation lying in one of the two diagonal planes of the cube with a clockwise or anticlockwise motion, with occasional brief reorientations. Proper orthogonal decomposition is applied to the joint velocity and temperature fields of an enriched database which captures the statistical symmetries of the flow. We found that each quasi-stable state consists of a superposition of four spatial modes representing three types of structures: (i) a mean-flow mode consisting of two stacked counter-rotating torus-like structures; (ii) two large-scale two-dimensional rolls (pair of degenerated modes) which form large-scale diagonal rolls when combined together; and (iii) an eight-roll mode that transports fluid from one corner to the other and strengthens the circulation along the diagonal. In addition, we identified three other modes that play a role in the reorientation process: two boundary-layer modes (pair of degenerated modes) that connect the core region with the horizontal boundary layers and one mode associated with corner rolls. The symmetries of the different POD modes are discussed, as well as their temporal dynamics. A description of the reorientation process in terms of POD modes is provided and compared with other modal approaches available in the literature. Finally, Galerkin projection is used to derive a POD-based reduced-order model. Unresolved modes are accounted for in the model by an extra dissipation term and the addition of noise. A seven-mode model is able to reproduce the low-frequency dynamics of the large-scale reorientations as well as the high-frequency dynamics associated with the large-scale circulation rotation. Linear stability analysis and sensitivity analysis confirm the role of the boundary-layer modes and the corner-rolls mode in the reorientation process.
$10^{7}$ and shows that the flow is characterized by four quasi-stable states, corresponding to a large-scale circulation lying in one of the two diagonal planes of the cube with a clockwise or anticlockwise motion, with occasional brief reorientations. Proper orthogonal decomposition is applied to the joint velocity and temperature fields of an enriched database which captures the statistical symmetries of the flow. We found that each quasi-stable state consists of a superposition of four spatial modes representing three types of structures: (i) a mean-flow mode consisting of two stacked counter-rotating torus-like structures; (ii) two large-scale two-dimensional rolls (pair of degenerated modes) which form large-scale diagonal rolls when combined together; and (iii) an eight-roll mode that transports fluid from one corner to the other and strengthens the circulation along the diagonal. In addition, we identified three other modes that play a role in the reorientation process: two boundary-layer modes (pair of degenerated modes) that connect the core region with the horizontal boundary layers and one mode associated with corner rolls. The symmetries of the different POD modes are discussed, as well as their temporal dynamics. A description of the reorientation process in terms of POD modes is provided and compared with other modal approaches available in the literature. Finally, Galerkin projection is used to derive a POD-based reduced-order model. Unresolved modes are accounted for in the model by an extra dissipation term and the addition of noise. A seven-mode model is able to reproduce the low-frequency dynamics of the large-scale reorientations as well as the high-frequency dynamics associated with the large-scale circulation rotation. Linear stability analysis and sensitivity analysis confirm the role of the boundary-layer modes and the corner-rolls mode in the reorientation process.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 24
- Cited by



