Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T11:43:51.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Pressure losses in grooved channels

Published online by Cambridge University Press:  14 May 2013

A. Mohammadi  and
J. M. Floryan
A. Mohammadi
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, Ontario, N6A 5B9, Canada
J. M. Floryan*
Affiliation:
Department of Mechanical and Materials Engineering, University of Western Ontario, London, Ontario, N6A 5B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effects of small-amplitude, two-dimensional grooves on pressure losses in a laminar channel flow have been analysed. Grooves with an arbitrary shape and an arbitrary orientation with respect to the flow direction have been considered. It has been demonstrated that losses can be expressed as a superposition of two parts, one associated with change in the mean positions of the walls and one induced by flow modulations associated with the geometry of the grooves. The former effect can be determined analytically, while the latter has to be determined numerically and can be captured with an acceptable accuracy using reduced-order geometry models. Projection of the wall shape onto a Fourier space has been used to generate such a model. It has been found that in most cases replacement of the actual wall geometry with the leading mode of the relevant Fourier expansion permits determination of pressure losses with an error of less than 10 %. Detailed results are given for sinusoidal grooves for the range of parameters of practical interest. These results describe the performance of arbitrary grooves with the accuracy set by the properties of the reduced-order geometry model and are exact for sinusoidal grooves. The results show a strong dependence of the pressure losses on the groove orientation. Longitudinal grooves produce the smallest drag, and oblique grooves with an inclination angle of 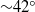${\sim }42\textdegree $ exhibit the largest flow turning potential. Detailed analyses of the extreme cases, i.e. transverse and longitudinal grooves, have been carried out. For transverse grooves with small wavenumbers, the dominant part of the drag is produced by shear, while the pressure form drag and the pressure interaction drag provide minor contributions. For the same grooves with large wavenumbers, the stream lifts up above the grooves due to their blocking effect, resulting in a change in the mechanics of drag formation: the contributions of shear decrease while the contributions of the pressure interaction drag increase, leading to an overall drag increase. In the case of longitudinal grooves, drag is produced by shear, and its rearrangement results in a drag decrease for long-wavelength grooves in spite of an increase of the wetted surface area. An increase of the wavenumber leads to the fluid being squeezed from the troughs and the stream being forced to lift up above the grooves. The shear is nearly eliminated from a large fraction of the wall but the overall drag increases due to reduction of the effective channel opening. It is shown that properly structured grooves are able to eliminate wall shear from the majority of the wetted surface area regardless of the groove orientation, thus exhibiting the potential for the creation of drag-reducing surfaces. Such surfaces can become practicable if a method for elimination of the undesired pressure and shear peaks through proper groove shaping can be found.

JFM classification

Flow Control: Drag reduction Flow Control: Flow Control Mathematical Foundations: Mathematical Foundations
Type
Papers
Information
Journal of Fluid Mechanics , Volume 725 , 25 June 2013 , pp. 23 - 54
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asai, M. & Floryan, J. M. 2006 Experiments on the linear instability of flow in a wavy channel. Eur. J. Mech. (B/Fluids) 25, 971–986.Google Scholar
Bazant, M. Z. & Vinogradova, O. I. 2008 Tensorial hydrodynamic slip. J. Fluid Mech. 613, 125–134.Google Scholar
Cabal, A., Szumbarski, J. & Floryan, J. M. 2001 Numerical simulation of flows over corrugated walls. Comput. Fluids 30, 753–776.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1996 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Cheng, Y. P., Teo, C. J. & Khoo, B. C. 2009 Microchannel flows with superhydrophobic surfaces: effects of Reynolds number and pattern width to channel height ratio. Phys. Fluids 21, 122004.Google Scholar
Choi, H., Moin, P. & Kim, J. 1991 On the effect of riblets in fully developed laminar channel flows. Phys. Fluids A 3, 1892–1896.Google Scholar
Chu, D. C. & Karniadakis, G. 1993 A direct numerical simulation of laminar and turbulent flow over riblet-mounted surfaces. J. Fluid Mech. 250, 1–42.Google Scholar
Darcy, H. 1857 Recherches expérimentales relatives au mouvement de l’eau dans les tuyaux. Mallet-Bachelier.Google Scholar
Davis, A. M. J. & Lauga, E. 2009 The friction of a mesh-like super-hydrophobic surface. Phys. Fluids 21, 113101.Google Scholar
Floryan, J. M. 1997 Stability of wall-bounded shear layers in the presence of simulated distributed surface roughness. J. Fluid Mech. 335, 29–55.Google Scholar
Floryan, J. M. 2002 Centrifugal instability of Couette flow over a wavy-wall. Phys. Fluids 14, 312–322.Google Scholar
Floryan, J. M. 2003 Vortex instability in a diverging–converging channel. J. Fluid Mech. 482, 17–50.Google Scholar
Floryan, J. M. 2005 Two-dimensional instability of flow in a rough channel. Phys. Fluids 17, 044101.Google Scholar
Floryan, J. M. 2007 Three-dimensional instabilities of laminar flow in a rough channel and the concept of hydraulically smooth wall. Eur. J. Mech. (B/Fluids) 26, 305–329.Google Scholar
Floryan, J. M. & Asai, M. 2011 On the transition between distributed and isolated surface roughness and its effect on the stability of channel flow. Phys. Fluids 23, 104101.Google Scholar
Floryan, J. M & Dallmann, U. 1990 Flow over a leading edge with distributed roughness. J. Fluid Mech. 216, 629–656.Google Scholar
Floryan, J. M. & Floryan, C. 2010 Traveling wave instability in a diverging–converging channel. Fluid Dyn. Res. 42, 025509.Google Scholar
Gamrat, G., Favre-Marinet, M., Le Person, S., Bavière, R. & Ayela, F. 2008 An experimental study and modelling of roughness effects on laminar flow in microchannels. J. Fluid Mech. 594, 399–423.Google Scholar
Hagen, G. 1854 Ueber den Einfluss der Temperatur auf die Bewegung des Wassers in Röhren. Math. Abh. Akad. Wiss. Berlin, 17–98.Google Scholar
Herwig, H., Gloss, D. & Wenterodt, T. 2008 A new approach to understanding and modelling the influence of wall roughness on friction factors for pipe and channel flows. J. Fluid Mech. 613, 35–53.Google Scholar
Husain, S. Z. & Floryan, J. M. 2010 Spectrally-accurate algorithm for moving boundary problems for the Navier–Stokes equations. J. Comput. Phys. 229, 2287–2313.CrossRefGoogle Scholar
Husain, S. Z., Floryan, J. M. & Szumbarski, J. 2009 Over-determined formulation of the immersed boundary conditions method. J. Comput. Meth. Appl. Mech. Engng 199, 94–112.Google Scholar
Kamrin, K., Bazant, M. Z. & Stone, H. A. 2010 Effective slip boundary conditions for arbitrary periodic surfaces: the surface mobility tensor. J. Fluid Mech. 658, 409–437.CrossRefGoogle Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.CrossRefGoogle Scholar
Lekoudis, S. G. & Saric, W. S. 1976 Compressible boundary layers over wavy wall. Phys. Fluids 19, 514–519.Google Scholar
Mason, J. C. & Handscomb, D. C. 2002 Chebyshev Polynomials. Chapman & Hall/CRC.CrossRefGoogle Scholar
Maynes, D., Jeffs, K., Woolford, B. & Webb, B. W. 2007 Laminar flow in a microchannel with hydrophobic surface patterned microribs oriented parallel to the flow direction. Phys. Fluids 19, 093603.Google Scholar
Miksis, M. J. & Davis, S. H. 1994 Slip over rough and coated surfaces. J. Fluid Mech. 273, 125–139.Google Scholar
Ming, Z., Jian, L., Chunxia, W., Xiaokang, Z. & Lan, C. 2011 Fluid drag reduction on superhydrophobic surfaces coated with carbon nanotube forests (CNTs). Soft Matter 7, 4391–4396.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J. M. 2012a Spectral algorithm for the analysis of flows in grooved channels. Intl J. Numer. Meth. Fluids 69, 606–638.CrossRefGoogle Scholar
Mohammadi, A. & Floryan, J. M. 2012b Mechanism of drag generation by surface corrugation. Phys. Fluids 24, 013602.Google Scholar
Moody, L. F. 1944 Friction factors for pipe flow. Trans. ASME 66, 671–684.Google Scholar
Morini, G. L. 2004 Single-phase convective heat transfer in microchannels: a review of experimental results. Intl J. Therm. Sci. 43, 631–651.Google Scholar
Morkovin, M. V. 1990 On roughness-induced transition: facts, views and speculations. In Instability and Transition (ed. Hussaini, M. Y. & Voigt, R. G.), ICASE/NASA LARC Series, vol. 1, pp. 281–295. Springer.Google Scholar
Ng, C. O. & Wang, C. Y. 2009 Stokes shear flow over a grating: implication for superhydrophobic slip. Phys. Fluids 21, 013602.Google Scholar
Nikuradse, J. 1933 Strömungsgesetze in Rauhen Rohren. VDI-Forschungscheft 361; also NACA TM 1292 (1950).Google Scholar
Nye, J. F. 1969 A calculation on the sliding of ice over a wavy surface using a Newtonian viscous approximation. Proc. R. Soc. A 311, 445–467.Google Scholar
Papautsky, I., Brazzle, J., Ameel, T. & Frazier, A. B. 1999 Laminar fluid behavior in microchannels using micropolar fluid theory. Sensors Actuators A 73, 101–108.Google Scholar
Ponomarev, I. V. & Meyerovich, A. E. 2003 Surface roughness and effective stick-slip motion. Phys. Rev. E 67, 026302.Google Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. Lond. 174, 935–982.Google Scholar
Richardson, S. 1973 On the no-slip boundary condition. J. Fluid Mech. 59, 707–719.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.Google Scholar
Saric, W. S., Carrillo, R. B. & Reibert, M. S. 1998 Nonlinear stability and transition in 3-D boundary layers. Meccanica 33, 469–487.Google Scholar
Sarkar, K. & Prosperetti, A. 1996 Effective boundary conditions for Stokes flow over a rough surface. J. Fluid Mech 316, 223–240.Google Scholar
Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
Sharp, K. V. & Adrian, R. J. 2004 Transition from laminar to turbulent flow in liquid filled microtubes. Exp. Fluids 36, 741–747.Google Scholar
Sobhan, C. B. & Garimella, S. V. 2001 A comparative analysis of studies on heat transfer and fluid flow in microchannels. Microscale Therm. Engng 5, 293–311.Google Scholar
Szumbarski, J. & Floryan, J. M. 1999 A direct spectral method for determination of flows over corrugated boundaries. J. Comput. Phys. 153, 378–402.Google Scholar
Szumbarski, J. & Floryan, J. M. 2006 Transient disturbance growth in a corrugated channel. J. Fluid Mech. 568, 243–272.Google Scholar
Tuck, E. O. & Kouzoubov, A. 1995 A laminar roughness boundary condition. J. Fluid Mech. 300, 59–70.Google Scholar
Walsh, M. J. 1980 Drag characteristics of V-groove and transverse curvature riblets. In Viscous Drag Reduction (ed. Hough, G. R.), vol. 72, pp. 168–184. AIAA.Google Scholar
Walsh, M. J. 1983 Riblets as a viscous drag reduction technique. AIAA J. 21, 485–486.Google Scholar