Article contents
Planar hydraulic jumps in thin film flow
Published online by Cambridge University Press: 05 December 2019
Abstract
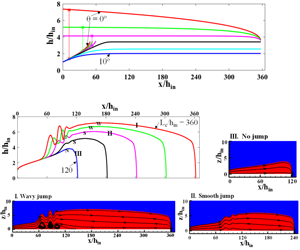
We reformulate shallow water theory to understand viscous shear induced natural hydraulic jumps in channels slightly deviated from the horizontal. One of the interesting contributions of the study is a modified expression for Froude number to predict jumps in inclined channels. The proposed Froude number is different from the conventional expression which incorporates channel inclination as a straight forward component of gravity. This highlights the complexity that a jump can generate even in single phase laminar flow. We also obtain an analytical expression for predicting jump strength and show that the scaling relationship originally proposed for jump location in horizontal channels is applicable for both upslope and downslope flows. As expected, upslope flow aids jump formation and beyond a critical adverse tilt, a submerged jump results in subcritical flow right from the entry. On the other hand, both Reynolds number and channel tilt suppress the tendency to jump in downslope flows and below a critical downslope inclination, the flow remains supercritical throughout the channel length. The film thickness for fully developed flow can be predicted from the exact solution of the Navier–Stokes equations. As the theory encounters a singularity in the jump region, numerical simulations and experimental results have been used to obtain additional insights into the physics of jump formation. They have revealed the existence of submerged jump, wavy jump, smooth jump and no jump conditions as a function of liquid Reynolds number, scaled channel length and channel inclination. Such a variety of jump geometries in planar laminar flow has not been reported earlier. Both theory and simulations also reveal that the linear free surface profile upstream of the jump is a function of Reynolds number only, while the downstream profiles can be tuned by changing both Reynolds number as well as the channel length and tilt over the range of parameters studied. We thus demonstrate that, despite the simplicity and the approximations involved, shallow water equations formulated assuming self-similar velocity profiles can elucidate the physics of planar laminar jumps over slight inclinations, difficult to avoid in practice. The analytical and simulated results have been extensively validated with experimental data obtained from a specially designed test rig which ensures laminar flow before and after the jump. To the authors’ knowledge, almost no experimental study has to date been reported on films ‘thin enough’ to remain laminar even after the planar jump.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 28
- Cited by


