Published online by Cambridge University Press: 24 June 2020
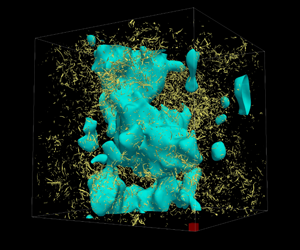
We study passive scalar fluctuations convected by statistically stationary homogeneous isotropic turbulence under a uniform mean scalar gradient. In order to elucidate the parameter dependence of small-scale statistics of scalar fluctuations, we conduct direct numerical simulations of passive scalar turbulence with 59 different combinations of Reynolds number and Schmidt number. For all the cases, we compute time-average statistics of various quantities, which include the scalar derivative skewness and flatness, the ratio of parallel-to-perpendicular scalar-gradient variances, and the anisotropy parameter recently proposed (Hill, Phys. Rev. Fluids, vol. 2, 2017, 094601). Notably, the degree of small-scale anisotropy of passive scalar fluctuation is characterised by a universal function of the Péclet number  $Pe_{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}}=u^{\prime }\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D705}$, where
$Pe_{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}}=u^{\prime }\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D705}$, where  $u^{\prime }$ is the root mean square velocity,
$u^{\prime }$ is the root mean square velocity,  $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$ the Taylor microscale of scalar fluctuation,
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$ the Taylor microscale of scalar fluctuation,  $\unicode[STIX]{x1D705}$ the mass diffusivity. In the definition of the Péclet number, the use of
$\unicode[STIX]{x1D705}$ the mass diffusivity. In the definition of the Péclet number, the use of  $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$, rather than the Taylor microscale of velocity fluctuation, is key to collapsing the data of different Reynolds and Schmidt numbers. When the Péclet number is low, large-scale anisotropic scalar structures emerge irrespective of the Reynolds number. These structures are elongated along the direction of the uniform mean scalar gradient, and their size is significantly larger than the integral length scale of velocity fluctuation.
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$, rather than the Taylor microscale of velocity fluctuation, is key to collapsing the data of different Reynolds and Schmidt numbers. When the Péclet number is low, large-scale anisotropic scalar structures emerge irrespective of the Reynolds number. These structures are elongated along the direction of the uniform mean scalar gradient, and their size is significantly larger than the integral length scale of velocity fluctuation.